三相输电线路中的损耗

我的一位同事提出了一个关于三相输电系统损耗的有趣问题。事实证明，输电线中导体的某些几何排列方式会导致导线之间的损耗不平衡，即使结构看起来是对称的。在这篇博客中，我们建立了一个简单的模型来证明这一点，并将介绍如何验证这个违反直觉的结果。

为什么损耗不平衡？

假设有三根相同的铜线，它们在一条水平线上等距排列，传输三相电，如下图左侧所示。那么，每根电线的损耗是多少？假设导线很长并且横截面恒定，我们将模型简化为二维横截面模型，在频域中求解。我们在 COMSOL Multiphysics^® 软件中对每根导线进行建模，使用线圈 域条件，并以复数形式定义相位彼此相差 120° 的三相交流电流。有关三相传输线建模的详细教程，请参阅之前的博客文章电缆建模系列教程。值得注意的是，通过所有三根导线的电流总和为零，因此我们不需要关心沿边界的任何电流返回路径。每根导线内的损耗分布如下图右侧所示。

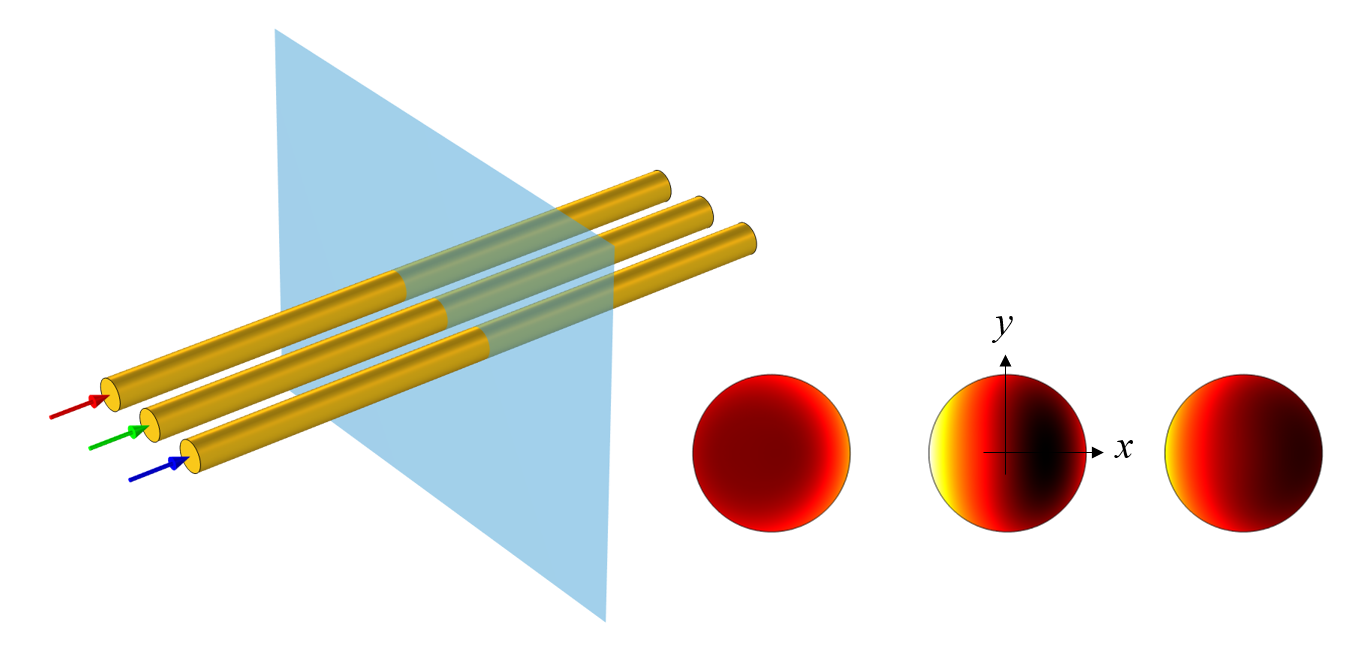
三根通有三相电流的平行导线的示意图，以及横截面的损耗图。

在这副图中，我们可以看到损耗分布关于 x 轴对称，但关于 y 轴不对称。这可能看起来不符合常理，因为导线的几何形状显然是关于两个轴对称。那么，如何解释这个结果呢？

一个损耗平衡的案例

有许多不同的方法来解释这种现象。这里，我们先改变几何，使之更加简单、易懂，然后再研究如何影响计算结果。我们把导体重新排列成一个等边三角形排列，如下左图所示。在这种情况下求解后发现，所有导体具有相同的总损耗和相同的损耗分布。另外，还值得注意的是，这些损耗分布是旋转对称的。也就是说，将磁场围绕中心点旋转120°可以得到相同的分布。现在，我们来努力理解为什么磁场是对称的，并看看这将如何帮助我们理解损耗不平衡现象。

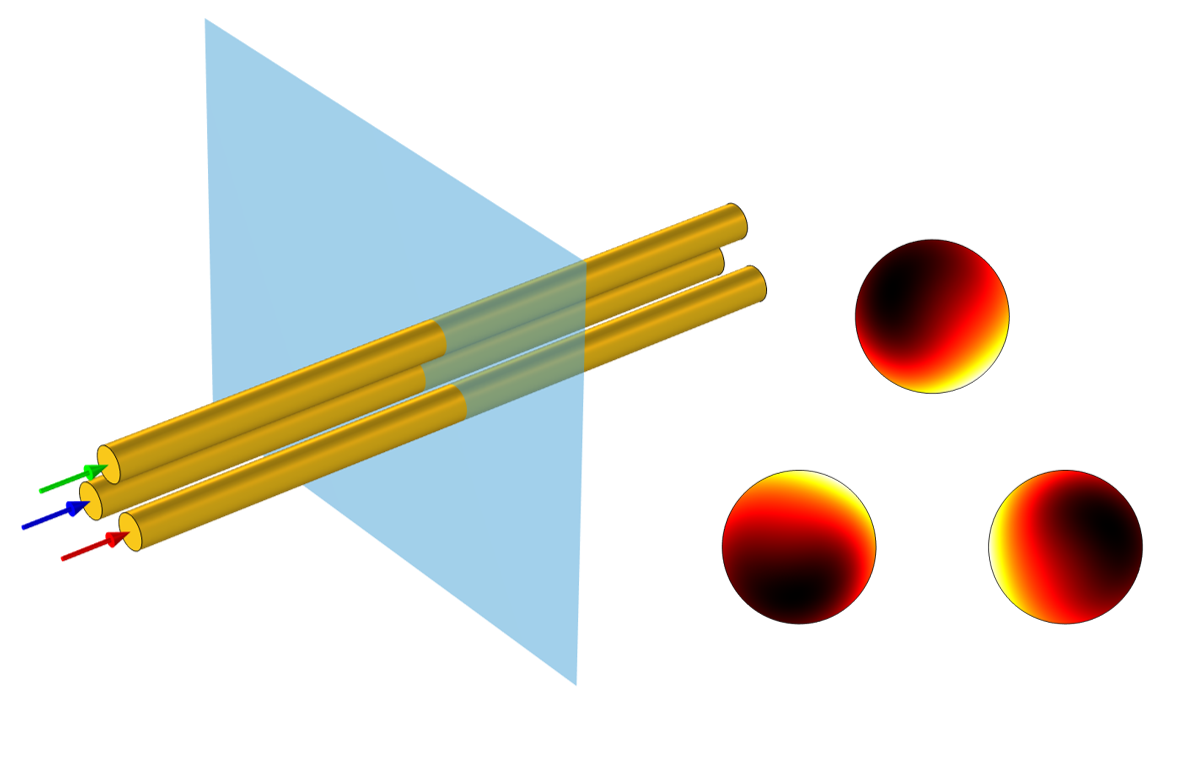
以等边三角形排列的三根导线表现出平衡的损耗。

当交流电流通过单根导线时，所产生的时变磁场会在导线内感应出电流。这些反向感应电流往往会与输入电流反向，尤其是在导线中心，这会导致所谓的集肤效应。除了导线本身的反向感应电流外，邻近效应还会导致输入电流在两个相邻导体中感应出电流。尽管没有正式的证明，我们称其为相邻输电线中的感应电流：

• 幅值相同，由于相邻的两个导体尺寸和间距相同
• 相位彼此相差 120°

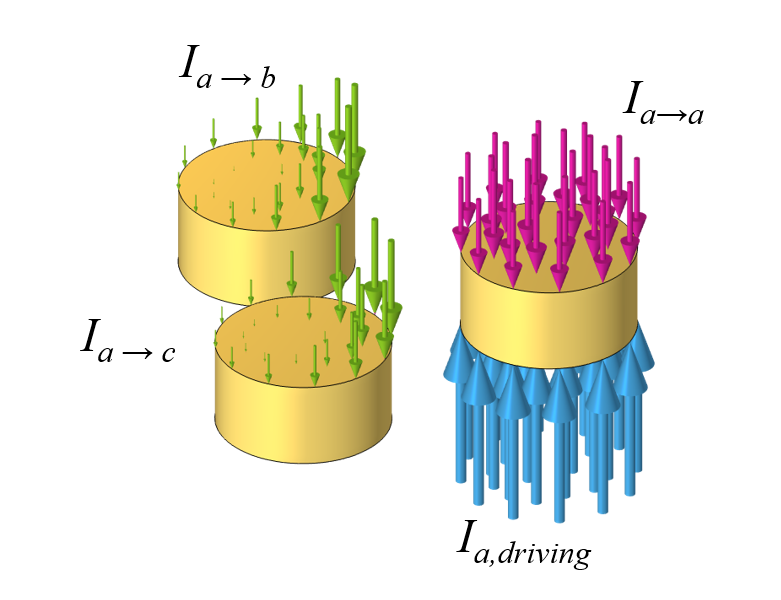
仅查看其中一根导线中的输入电流，它会在导线本身以及两条相邻的导线中产生感应电流。

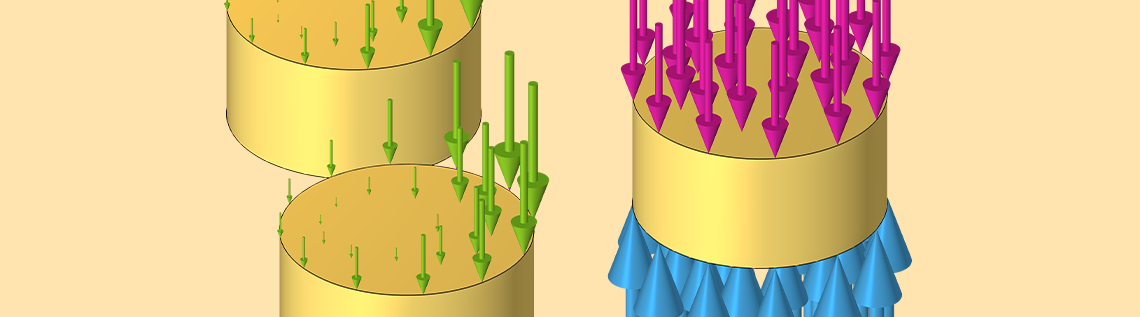
当三相电流通过所有三根导线时，通过这三根导线中一根导线的总电流是该导线中的输入电流、反向感应电流以及来自相邻导线的感应电流总和，例如，I_{a,tot}=I_{a,driving}+I_{a \rightarrow a }+I_{b \rightarrow a}+I_{c\rightarrow a }。引起三相电流所需的外加电压与输入电流成正比，由下式给出：V_{a}=I_{a,driving} R，其中 R 是直流线电阻。当使用线圈 特征描述这些导线时，方程组中会添加一个额外的全局 方程。这将求解能产生所需总电流的电压。每根导线的总损耗由下式给出：Q_a = \frac{1}{2} \Re \left( I_{a,tot}V_a \right)，其中电流和电压是复数形式并且相位相差 120°。

现在，让我们在复平面中绘制这些电流，这可以帮助我们观察这三个反向感应电流如何加和为总电流。实际上，我们并不知道这些项的真实幅度或相位，但我们知道来自两条相邻导线的感应电流的相位彼此相差 120°。我们还可以合理地假设电流的相对大小为：|I_{a,driving}| > | I_{a \rightarrow a } | > | I_{a \rightarrow b}| = |I_{a\rightarrow c } |。有了这些信息和假设，我们就能够制作下面草图。

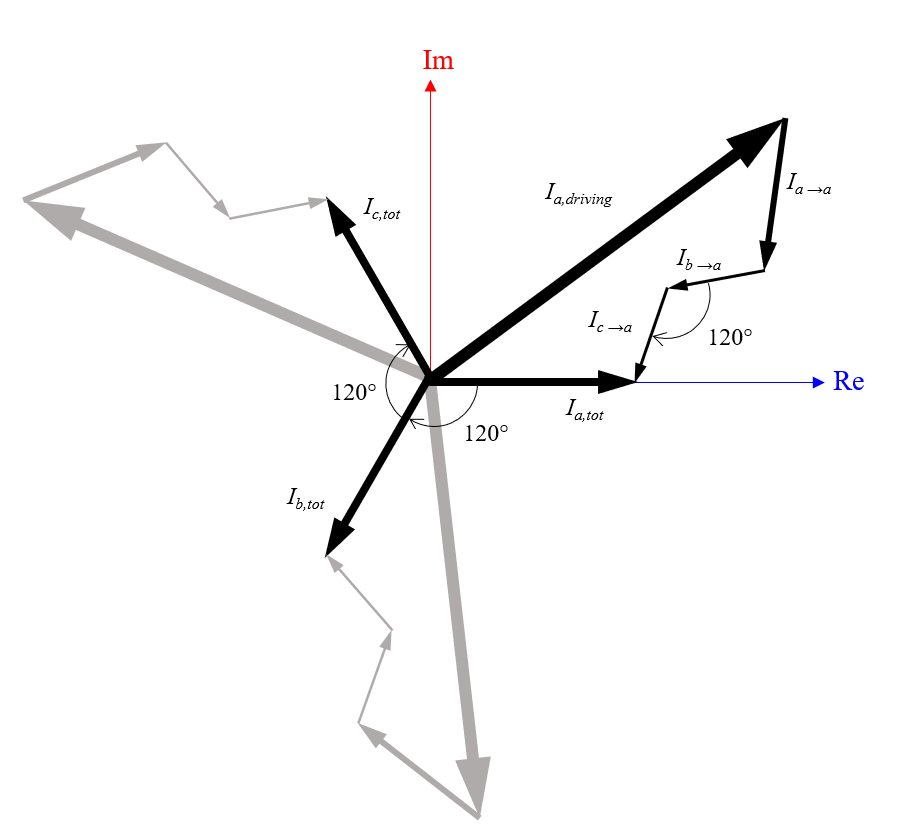
对输入电流、反向感应电流和其他导线感应的电流求和将得出总电流。对于以等边三角形排列的相同导线，这三个电流的幅值相等且相位相差 120°。

考虑施加在所有导线上的复数电压，并考虑当将导线从等边排列变为线性排列时会发生什么。我们将中心导线标记为 a。反向感应电流，例如， I_{a \rightarrow a }，不会改变，并且从中心导线到外侧导线的感应电流在大小上仍然相等： | I_{a \rightarrow b}| = |I_
{a\rightarrow c }|。从一侧的导线到中心导线和另一根外侧导线的感应电流将不同： | I_{b \rightarrow a}| \ne |I_{b\rightarrow c }| 和 | I_{c \rightarrow a}| \ne |I_{c\rightarrow b }|。但是，外侧两根导线之间的感应电流的大小是相同的 — | I_{b \rightarrow c}| = |I_{c\rightarrow b}|—，并且相对相位保持不变。我们现在可以绘制总和并比较三角形和线性排列。

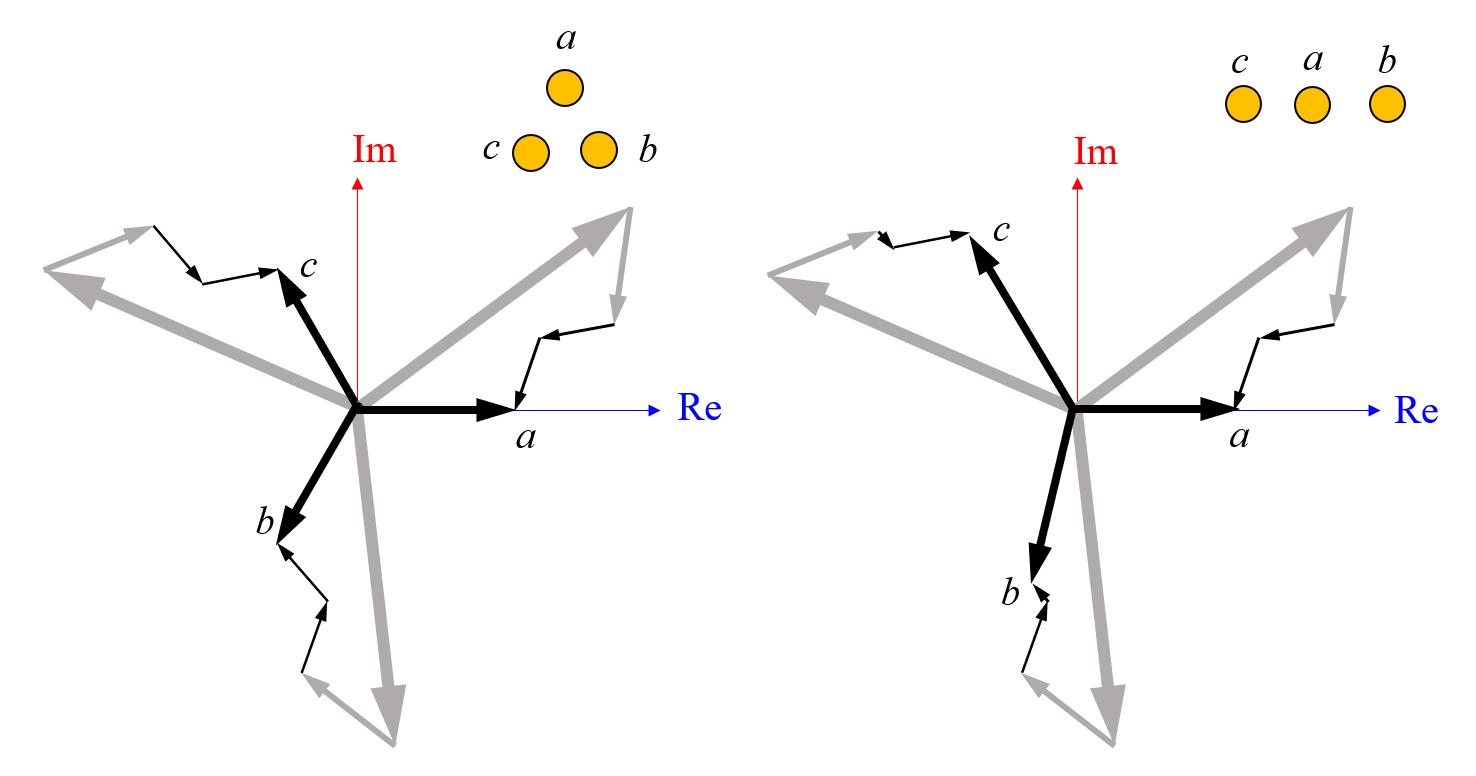
在左侧图中，三角形配置的电流总和是对称的。在右侧图中，电压保持恒定，但导线变为线性配置，因此感应电流的大小不同，对称性被打破。

可以看到，施加三相平衡的电压必然导致电流不平衡。或者，如果我们回到原来的情况并想要获得平衡的电流，那么施加的电压必须都不同。因此，损耗不可能相同。

结束语

如果要对这个系统进行物理验证，最容易想到的方法是测量每根电线的总损耗。外部两根导线上实验测量的总损耗几乎 相同，很容易将这种微小差异归因于实验误差。只有当查看数值计算的损耗分布时，如文章开始的图片中那样，差异才会变得更加明显。然而，实心导线内部损耗分布的试验验证将非常困难，而且可能从来没有人做过这样的试验。

还值得注意的是，思考问题有多种不同的方式，这只是其中的一种方式。还可以这样思考，即尽管在初始情况下 x 轴和 y 轴存在几何对称性，但对称条件只允许相位相差 180° 的场，即双重对称。具有 相位相差120°导线的解需要三重对称，例如等边排列。同样重要的是，要承认我们在这里展示的不是正式的证明，即使是最基本的结果也应该质疑，无论它们在视觉上多么有吸引力。所以，虽然我们已经提出了一些非正式的证明，但这是否足够？

另一个证明是模型本身。我们开始使用的初始模型很简单：线性布置的三根导线，流通三相电流，通过有限元方法在没有奇点的域上求解。有时，即使是简单模型的结果也会与我们的直觉不一致。这通常会导致人们怀疑模型中的错误，这当然是合理的，因为对每个模型我们都应该带着一点怀疑和严格的验证和确认过程来处理。我们甚至可能会怀疑有限元方法本身，尽管它是数学物理学中最常用和充分验证的方法之一。

最后，我们绝不能落入过于相信直觉的陷阱。科学中一些最瞩目的发现始于意想不到的观察，所以请始终保持开放的心态！