如何使用 COMSOL Multiphysics 模拟残余应力

今天，我们将介绍结构力学中残余应力的概念，并以金属的深拉深成型工艺为例，探讨如何计算残余应力。我们先通过一个经过或未经过硬化的弯曲梁示例，解释如何计算和分析残余应力，然后介绍一个钣金成型模型。

什么是残余应力？

残余应力是指弹塑性结构卸载后仍留在结构内的自相平衡的应力。机械零件的制造过程会引入残余应力，并将影响零件的疲劳、失效甚至腐蚀行为。

不受控制的残余应力会导致结构过早失效。残余应力会改变性能，甚至会导致产品故障，但实际上某些应用是需要它的。例如，像智能手机屏玻璃这种脆性材料，在其制造过程中通常会在表面产生压缩残余应力，以避免裂纹扩散。

因此，残余应力对机械学应用整体起着着重要的作用。只有对这些应力进行定性和定量分析，才能确定最适合特定应用的制造工艺。这些分析还可以帮助探索实现产品可靠性所需的最佳材料用量或最合适的形状设计，来避免故障或失效。

纯弯曲状态下的梁

以一个矩形截面的细长梁为例，梁的厚度为 a，宽度为 b。梁的左侧被固定，右侧自由端上施加了一个弯矩，如下图所示。

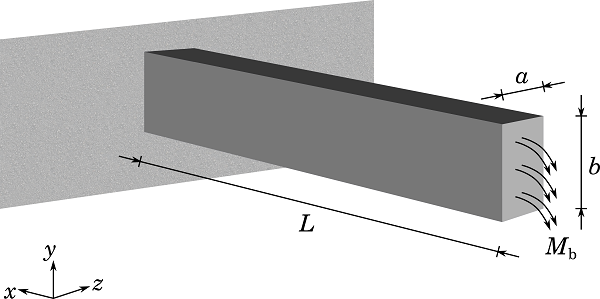
计算残余应力

基于梁理论，示例中的弯矩恒定不变，应力由下式表示：

(1)

式中，I_z 是关于 z 轴的惯性矩。

随着 M_\mathrm{b} 的增加，梁首先表现出弹性行为，当达到其屈服弯矩 M_y 后， 开始表现出塑性行为，最终产生一个弹塑性截面。当塑性区扩展至整个横截面时，就可以确定梁所能承受的极限弯矩 M_\mathrm{ult}。我们假设在这个时刻梁会坍塌，表现出理想塑性行为梁。

梁的外层纤维将首先达到屈服点，内部纤维则芯保持弹性。因此，由之前施加于梁外层纤维的方程推导出第一个屈服弯矩：

(2)

式中，\sigma_\mathrm{yield} 是屈服应力。

在弹塑性时刻 M_\mathrm{ep} < M_\mathrm{ult}，梁每一侧的塑性区沿厚度方向延伸距离 h_\mathrm{p}，如下图所示。

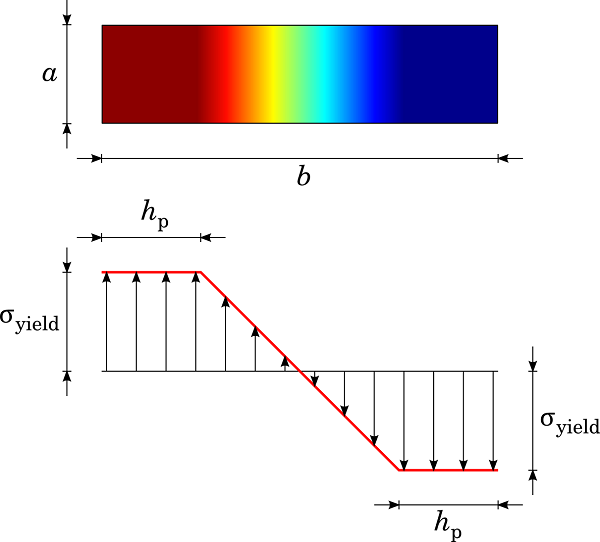
矩形截面梁两侧的塑性区穿透。

总弯矩可分为弹性部分 M_e，和塑性部分 M_p，即：

(3)

式中，I_\mathrm{e}=\frac{a(b-2h_\mathrm{p})^3}{12} 是内部纤维芯在 z 轴方向的惯性弹性矩。

合并最后两个表达式，得到以下方程：

(4)

理想弹塑性梁 M_\mathrm{ep} 卸载后，梁横截面仍留存残余应力 \sigma_r。随着弹性弯曲应力 \sigma_\mathrm{e} 的恢复，梁尝试恢复其初始形状。这里，假设加载 M_\mathrm{ep} 后，会产生纯弹性卸载，相应的产生弹塑性应力 \sigma 。残余应力可由弹塑性应力与纯弹性应力之差计算，纯弹性应力指不涉及塑性行为时产生的应力。

(5)

由弹性弯曲理论，推导出恢复的弹性应力：

(6)

假设出现理想塑性行为，塑性区的应力 \sigma（也就是 \frac{b} {2}-h_\mathrm{p} \le |y| \le \frac{b}{2}）保持不变，等于 \sigma_\mathrm{yield}。因此，根据方程（5），残余应力可以写成：

(7)

在弹性区，也就是（0 \le |y| \le \frac{b} {2}-h_\mathrm{p}），由梁理论推导出施加的应力为：

(8)

因此，可以推导出残余应力：

(9)

当外部力矩被移除后，由于塑性变形，梁将仍保留永久性位移，但同时也会部分恢复一些峰值载荷状态下的位移。在需要可控的塑性变形应用中，这种 回弹 效应非常重要。

在模拟二维梁时，我们可以选择采用泊松比 \nu=0 的 平面应力 假设 ，与不考虑泊松效应的一维梁理论相匹配。在 COMSOL Multiphysics 中，可以通过选择二维空间维度和 固体力学 接口，模拟二维平面应力。

在 COMSOL Multiphysics 中计算残余应力

接下来，介绍如何在二维中使用 固体力学 接口计算梁截面的残余应力。

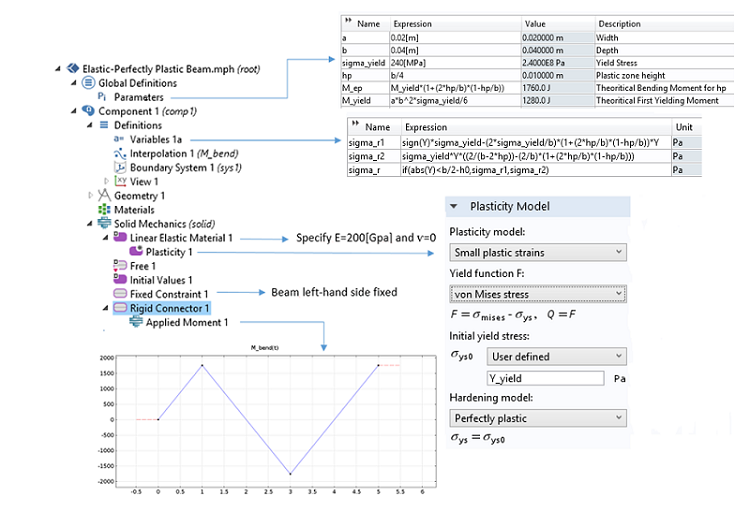
使用 固体力学 接口建立的二维梁模型的截图。

根据以上截图可知，我们定义了一些变量来评估上文中推导出的残余应力。这些理论值将用于对比计算结果和理论结果。

施加的弯矩是逐渐递增的。为了考虑梁厚度上可能发生的单轴塑性行为，我们添加了一个塑性节点。当 \sigma_x 达到临界值 \sigma_\mathrm{yield} 时，塑性流动就会开始。每一根已经达到临界值的纤维在加载过程中将仍保持应力恒定不变。

由下图可以看到，沿横截面 Y 轴 的应力分布。对于厚度为 h_\mathrm{p}=\frac{b} {4}=0.01 \ \mathrm{m} 的塑性区，施加的弯矩由 方程（4） 计算得出。由蓝色曲线可以看出，COMSOL Multiphysics 的模拟结果与计算结果完全一致。红色曲线表示一个加载-卸载循环后的残余应力。请注意，也可以用理想弹塑性曲线（蓝色）中减去弹性曲线（绿色）获得残余应力。

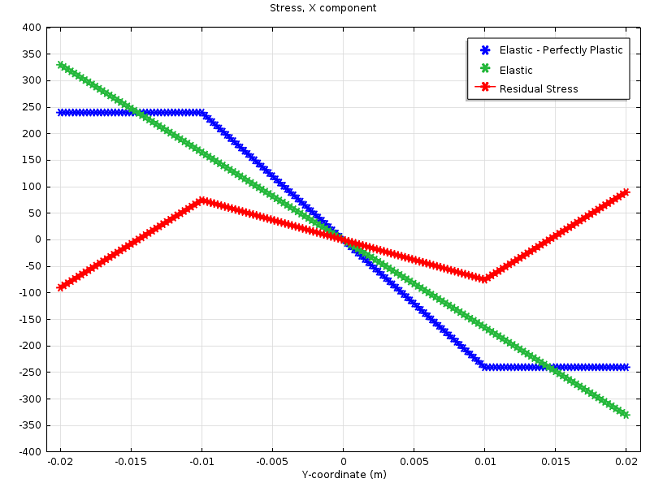
弹塑性加载、弹性加载以及卸载后的应力值。

方程（7） 和 方程（9） 作为定义变量，并与 COMSOL Multiphysics 的计算结果进行比较。如上文中的截图所示，可以使用 if() 算子创建一个 “开关”，这样代表残余应力解析解的两个表达式就被集中在一个表达式中了。下图显示了两次加载-卸载循环后解析的和模拟的残余应力。

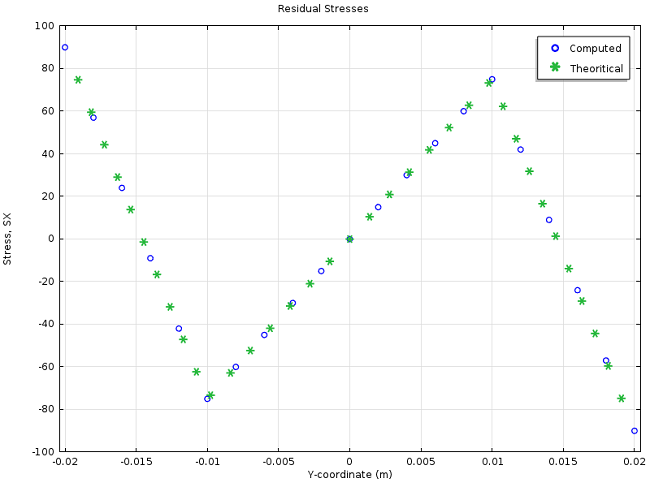
解析的与模拟的残余应力。

使用 COMSOL Multiphysics，能够对特定材料的滞后周期进行建模。如下图所示，在完全塑性行为的情况下，第二次载荷循环已经施加了一个稳定的应力-应变响应，代表每个连续的载荷循环。例如，你可以使用这些载荷循环来进行疲劳分析。

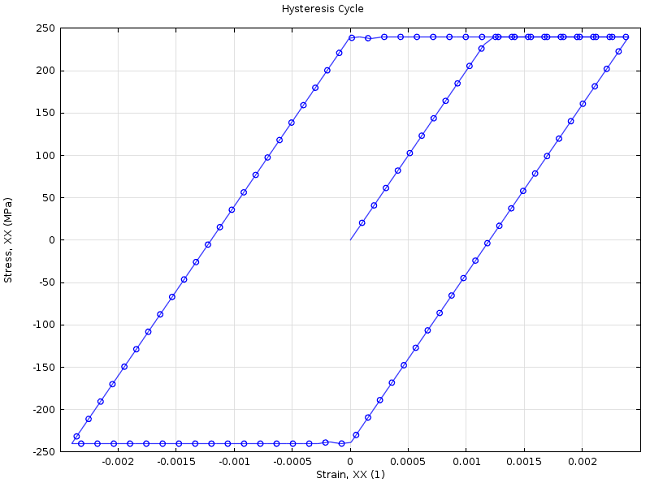
三次加载-卸载循环后的磁滞行为。

最后，我们来探讨应变硬化行为如何影响残余应力和加载-卸载循环。截至目前，我们一直在讨论理想塑性材料。无论循环次数多少，也无论施加的是拉伸载荷还是压缩载荷，屈服应力都保持不变。只要不发生反向屈服，方程（5） 就有效。因为卸载过程中的反向塑性变型对性能有负面影响，所以弄清楚在什么条件下可能发生反向屈服非常重要。

对于延展性材料，先在一个方向逐渐增加应力（例如拉伸）后卸载，然后在相反的方向加载时，其行为会有所不同。此时的 压缩 屈服应力比 拉伸 时测得的要低。这就是所谓的 Bauschinger 效应。同样，初始压缩会降低拉伸屈服应力。下图显示了这种效应在两次应力循环中的表现：

延展性材料先在一个方向受到越来越大的应力（例如拉伸），然后卸载，当在相反方向上加载时，其行为会有所不同。人们发现，现在的压缩 屈服应力比拉伸 时测量的要低。这就是所谓的 Bauschinger 效应。同样地，初始压缩提供了一个较低的拉伸屈服应力。下图显示了两次应力循环下的这种效应：

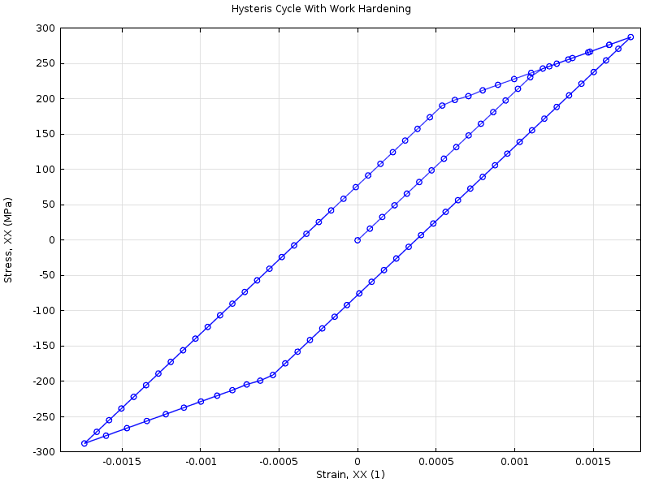
运动应变硬化的滞后效应。

接下来，我们继续讨论残余应力非常重要的更复杂的机械过程：钣金成型工艺。

金属冲压成型

冲压成型是一种应用广泛的钣金成型工艺。通过成型和拉伸工艺的塑性变形，金属板工件将在模具周围被永久塑形。坯料支架对坯料施加压力会导致金属板在模具的反作用下流动。

为了避免裂纹、撕裂、褶皱和过度变薄和拉伸，我们可以使用仿真进行评估。仿真也可以预测和克服回弹现象，即当成型过程结束，成型工具被移除后，工件将如何恢复到其初始形状。回弹会导致成型的坯料达到意想不到的翘曲状态。为了应对这种影响，我们可以对板材进行过度弯曲。因此，在模具、冲头和坯料的制造过程中，不仅要考虑与物体的实际形状一致，还要考虑回弹。

此研究中，板材由铝制成。我们使用一个包括各向同性硬化的Hill正交弹塑性材料模型表征塑性变型。据观察，在深拉伸工艺中，金属板材不再表现为各向同性行为。沿厚度方向增加的塑性变形越来减少。因此，在板材的冲压成型和深拉伸工艺中，需要板材具有在平面内是各向异性，在垂直方向具有逐渐增加的强度，也称为 横向各向异性。

下图是我们模拟的拉深工艺中使用的成型工具。

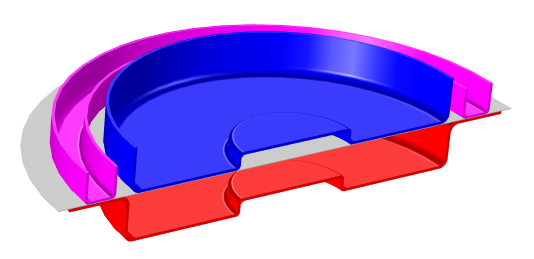
成型工具：模具用红色表示，冲头用蓝色表示，支架用粉红色表示，坯料用灰色表示。

如上所述，仿真能够同时模拟在制定这种机械过程中需要考虑的多个任务。例如，为了防止金属板断裂，可以适当对模具和冲头的角半径进行优化。为了获得冲头和模具之间所需的间隙，来避免金属坯料被剪切，也可以通过仿真优化。

最具挑战性的任务是计算出金属板应该过度弯曲多少。当板材成型后，残余应力会使材料回弹到其初始位置，必须对板材进行过度弯曲以使其达到所需的弯曲角度。因此，必须准确地模拟残余应力，以避免过高或过低估计回弹现象。

下面两个动画显示了钣金成型以及金属坯料的回弹现象。

RZ 平面 上的回弹现象。

钣金成型过程仿真。

当结构承受其他机械载荷时，残余应力的叠加会降低结构的可靠性，甚至导致不可逆的损伤。因此，必须尽可能地释放残余应力或对其进行管理，以使结构能够承受施加的外部载荷。下图显示了完成深冲压外圈工艺后，弯曲区域周围残留的 Hill 有效残余应力。

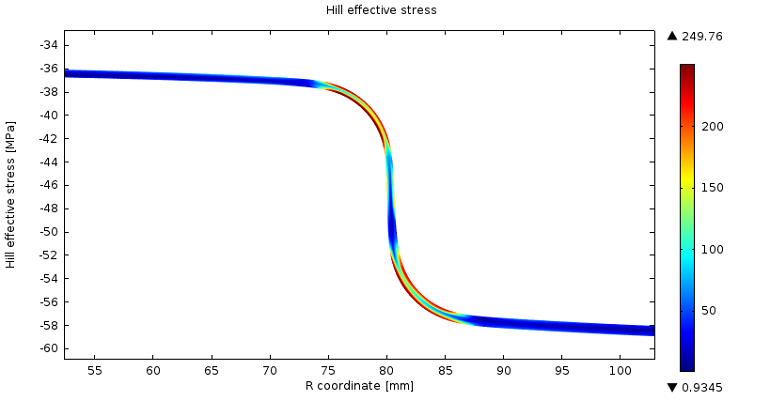
结论与延伸阅读

这篇博客，我们对结构力学中的残余应力进行了研究。介绍了在弯曲梁示例中被首次应用的残余应力的定义。然后，使用 COMSOL Multiphysics 模拟了这个弯曲梁示例，并将结果与使用梁理论解析的解进行了对比。最后，探讨了钣金成型案例模型，讨论了残余应力的重要性。我们发现，任何机械过程都会产生残余应力，因此必须特别注意适当释放，或者至少要确保其不会造成任何损伤。

点击下方链接，了解更多相关产品的信息：

• 结构力学模块
• 非线性结构材料模块