
室内声学建模和仿真的一个挑战是准确模拟一个房间内全部频率范围内的声学性能。这篇文章讨论了在 COMSOL Multiphysics® 软件中对室内声学进行建模的一种混合方法,就是将多种方法的结果集成到一个模型中,来提高准确性并确保方法的可行性。接下来,我们来看看如何做到这一点。
室内声学回顾
在上一篇关于使用 COMSOL Multiphysics 对室内声学进行建模的博客中,我们介绍了 COMSOL 软件的声学模块中可用于建立封闭空间的声学模型的多种方法。文章讨论了:
- 如何使用压力声学 接口模拟模态行为
- 如何使用射线声学 接口模拟高频行为
- 如何使用声学扩散方程 接口模拟高频行为
今天,我们将讨论如何结合使用前两种方法获得一个房间内的宽带脉冲响应。
室内脉冲响应
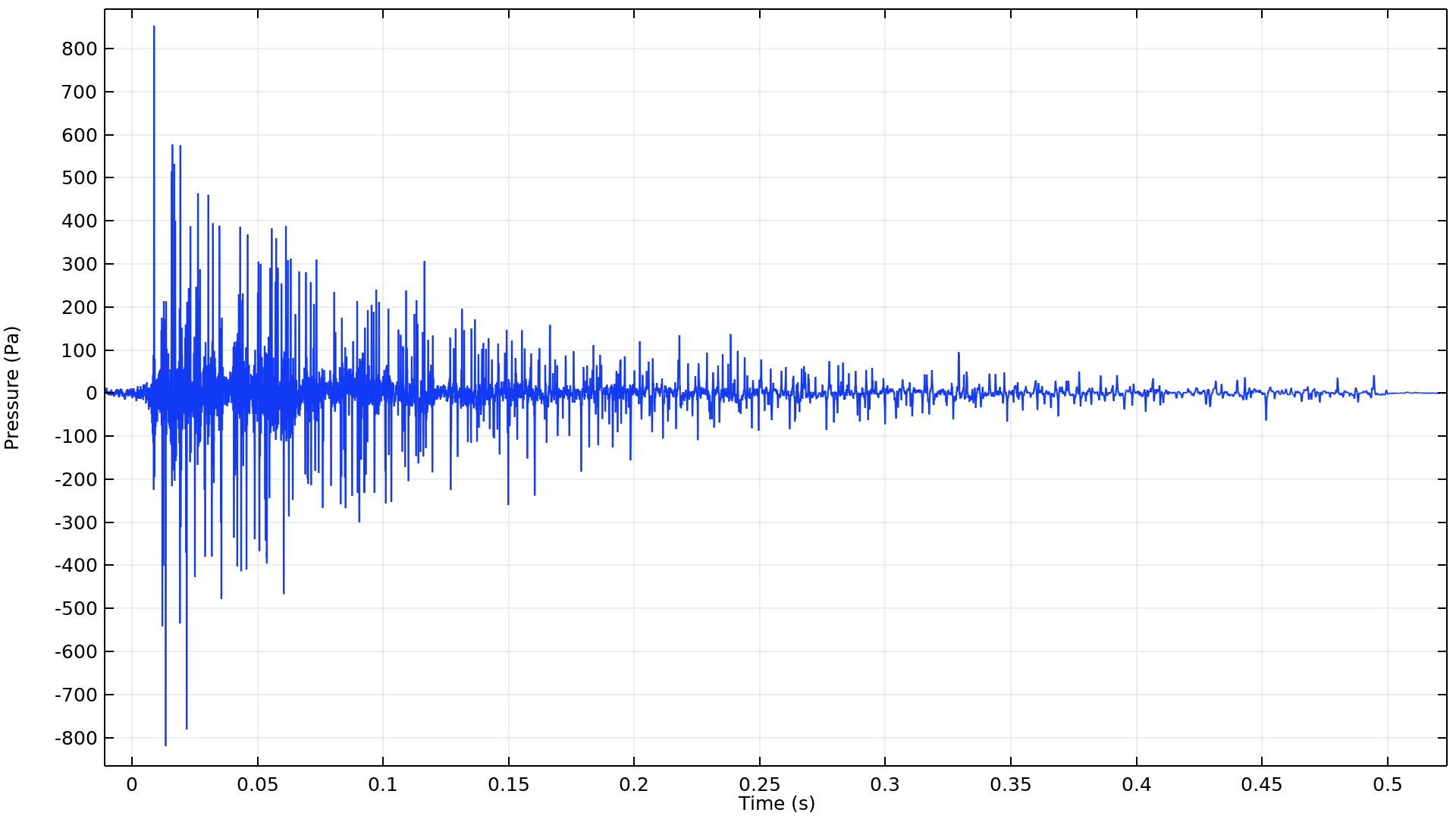
想象一下,在一个房间里弹起一个充满空气的气球,并在房间的某个位置放置一个麦克风记录与时间相关的声压。麦克风将收到来自第一个波前的直接声音,以及从墙壁、地板、天花板和其他物体上传播和反弹的所有波反射信号的叠加。声音通常会被不同的材料吸收,例如地毯、家具和天花板,最终会完全消失。麦克风记录的声压与时间的关系信号被称为该测量位置的室内脉冲响应。这是一个非常重要的室内声学描述量,因为它可以告诉我们很多关于房间内的声学性能。
左:射线声学模型的结果显示了从声源到麦克风位置的一小部分射线的路径。右:室内脉冲响应示例。
对房间进行建模
对一个房间的声学性能进行建模时,为了确定建模方法的准确性和可行性,仿真工程师必须同时关注声学特性和几何尺度。在 COMSOL 声学模块中,可以使用压力声学,频域 接口通过有限元方法对房间的低频模态行为进行建模。然而,由于网格的要求,这种方法在高频下计算成本很高。我们可以通过射线声学 接口的射线追踪方法对房间的高频混响行为进行建模。虽然这种方法通常计算效率高,但射线追踪不是基于波的方法,不会捕获模态行为。为了准确模拟房间的脉冲响应,两种模型都可以在各自的频率范围内运行,并可以结合使用两种方法来获得全部频率范围内的响应。
考虑一个 4.7m x 4.1m x 3.1m 的矩形房间。本例中所有的壁都使用与频率相关的吸收系数进行建模。该模型的目标是确定位于坐标(3,3,2)m 处的麦克风的脉冲响应。事实证明,对于一个考虑“轻微”吸收壁的单极脉冲源,房间内任何一点的压力都有三维解析解。遵循参考文献1和 参考文献2中的符号标记,任何一点的压力 P(r) 都可以用格林函数 G(r,r_0) 来表示,格林函数由在接收器 (r) 和源 (r0) 位置计算的无阻尼房间模式形状和一个与频率相关的阻尼项 \tau_{mnp} 构成。表达式为:
式中,\rho_0 是密度,\omega 是频率,Q 是单极域源体积速度。格林函数表示三个正交笛卡尔方向上模态的三次求和,指数 m n p 表示不同的模态。\psi s 表示模态形状,k_{mnp} 是模态的余弦函数乘积,\Lambda_{mnp} 是体积空间 V 的模态整数因子。波数为 k。关于分析解的完整说明,请查阅参考文献1和参考文献2。对于这个建模方案,定义解析解的变量已经添加到组件1 定义变量1-解析解 中。
就像我们之前的博客中所讨论的,模态和混响房间行为之间没有明确的过渡频率,但可以根据Schroeder提出的标准(参考文献 3,4)进行估计。在这个案例中,Schroeder 频率接近 370Hz,并通过全局定义 射线参数计算。上面的解析解将作为参考解与数值模型进行比较。
压力声学
理想情况下,我们可能希望在全部频率范围内使用基于波的方法对房间内的声学性能进行建模,但由于网格要求,这在高频下不可行。我们知道低于 Schroeder 频率的单个模态的贡献占室内响应主导地位,因此选择使用略高于 Schroeder 频率的最大频率求解压力声学:在这个案例中,频率高达 500Hz。压力声学模型的设置包括:
- 含压力声学、频域 接口的 3D 组件
- 含恒定功率的单极点源
- 指定壁面的频率相关阻抗条件(吸收系数)
- 能解析空气中 500Hz 以下的波长的体网格
- 频域研究
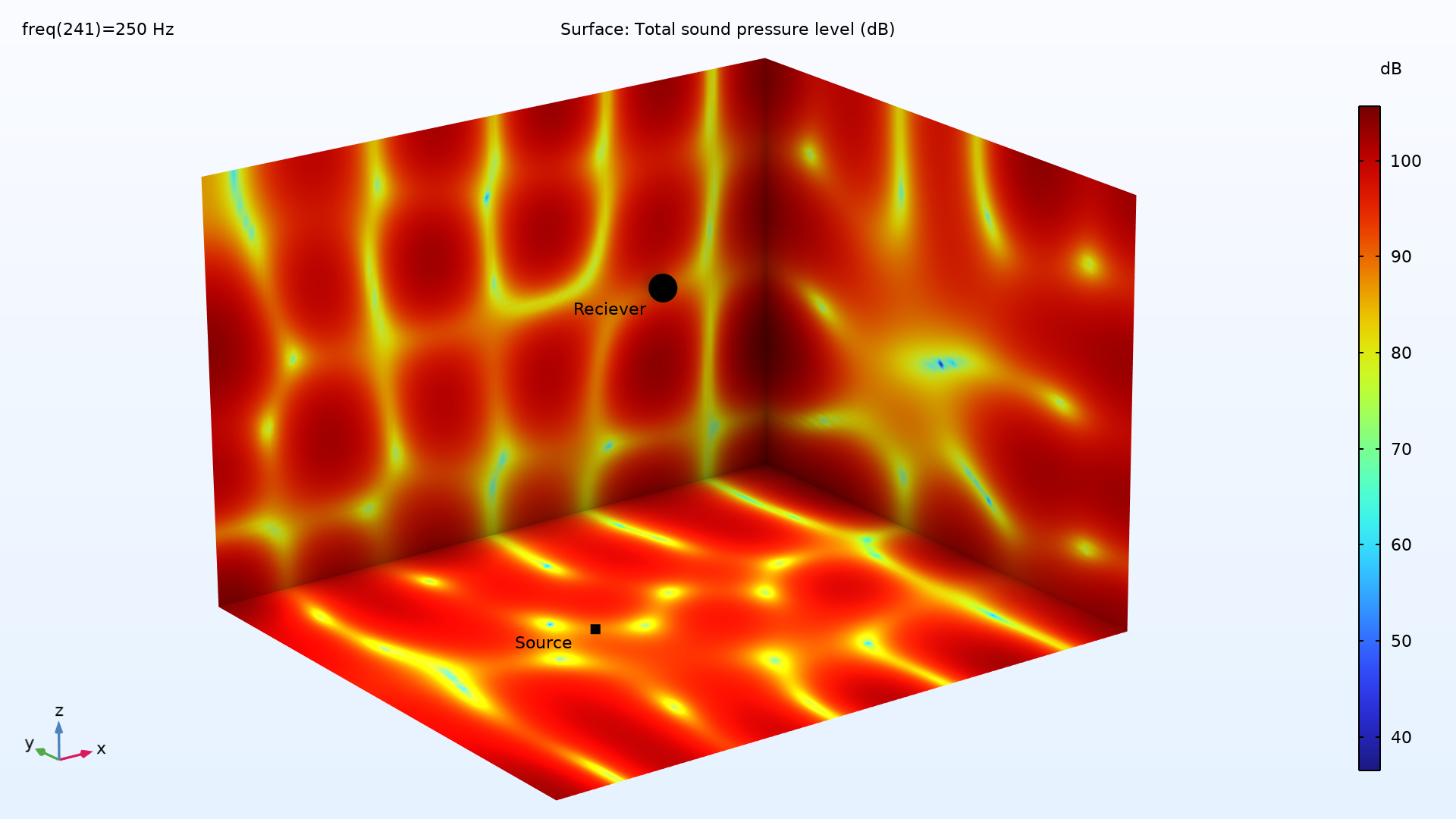
矩形房间三面壁上的声压级(分贝的参考值为 20μPa),频率为 250Hz。
上图示例显示了房间壁上的总声压级分布。使用这种方法,我们已经模拟了房间内声学的低频行为(低于 500Hz)。为了模拟房间内声学的高频行为,我们将切换到射线声学。
射线声学
射线声学模型设置如下:
- 使用射线声学 接口添加 3D 组件
- 使用频率相关吸收系数指定壁面条件
- 使用从栅格释放 条件,按照指定功率从源点释放 8000 条射线
- 如果功率水平低于阈值,使用射线终止 标准停止追踪射线,从而降低自由度
- 使用高达 4000kHz 的超过 1/3 倍频程带频率的参数扫描进行射线追踪研究
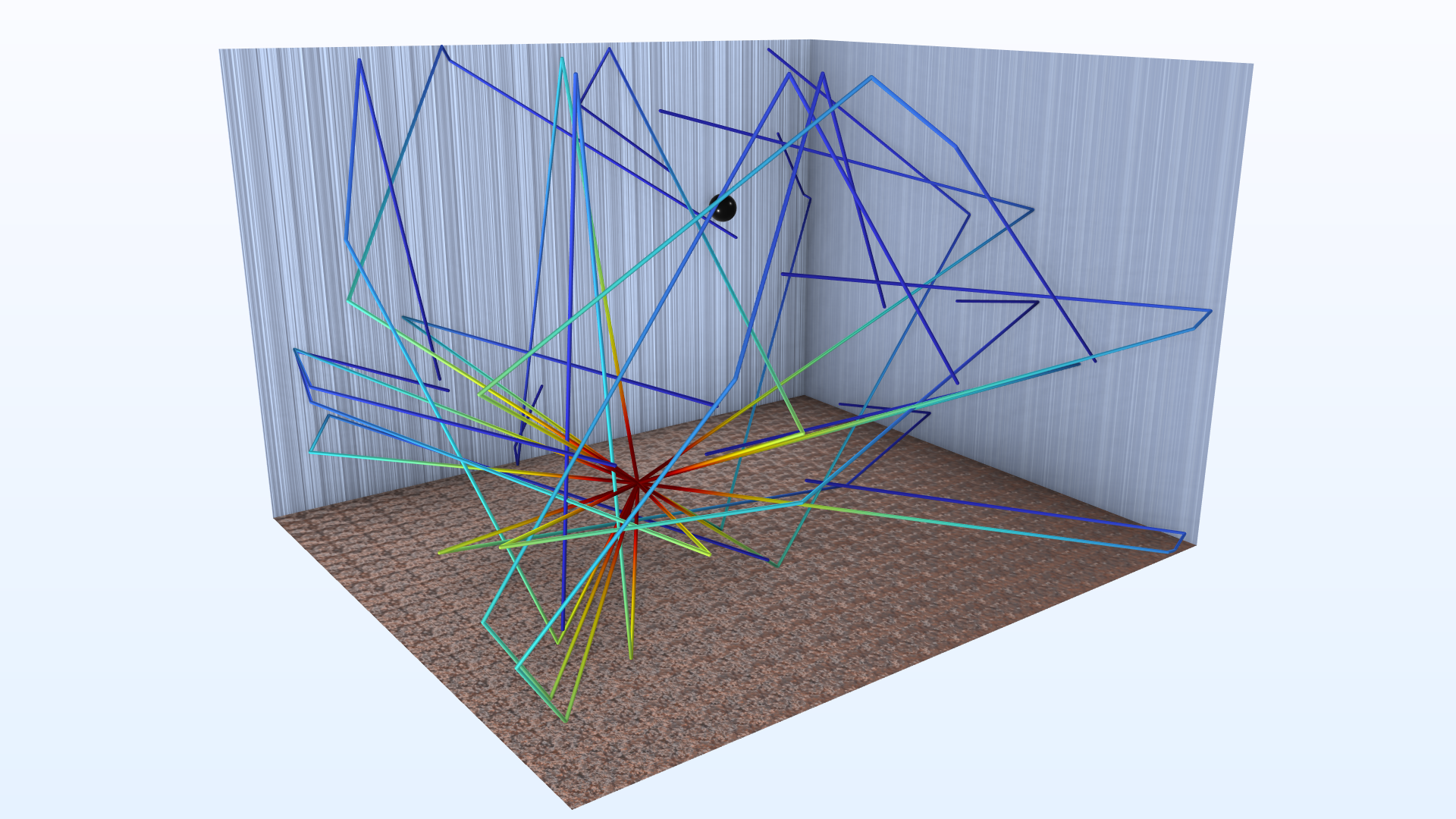
下图显示了从点光源释放出射线时的屏幕截图。请注意,为了可视化图像,下面仅显示了一小部分光线。(y 坐标上小于源位置的射线被隐藏。)

3 ms 时的射线轨迹显示了从单极点源释放的射线。色阶代表射线压力,单位为 Pa。
射线追踪研究不是以精细步长运行的。那么脉冲响应如何计算的呢?在 COMSOL Multiphysics 中,有一个专用的 接收器 数据集和一维脉冲响应 绘图可用于此计算。该绘图组采用 1/3 倍频程输入,例如射线功率、频率、反射次数和流体特性,并重构频率范围内的脉冲响应。目标是获得一个新信号,当对输入的倍频程频段进行平均时,该信号的能量含量与真实信号相同。这是通过将脉冲信号与选定的红外滤光核(默认是带有 Kaiser 窗口的砖壁)进行卷积,然后将所有频段上所有射线的贡献进行汇总来完成的。有关重构的更多信息,请查看声学模块用户指南。
下图显示了麦克风位置处的声压级。由于单极点源代表一个时间上的脉冲,因此房间的脉冲响应也可以在频域中解释,其中源是频率范围内的一个宽带激励。(狄拉克 δ 函数在时间上的傅里叶变换是一个与频率有关的恒定函数。)
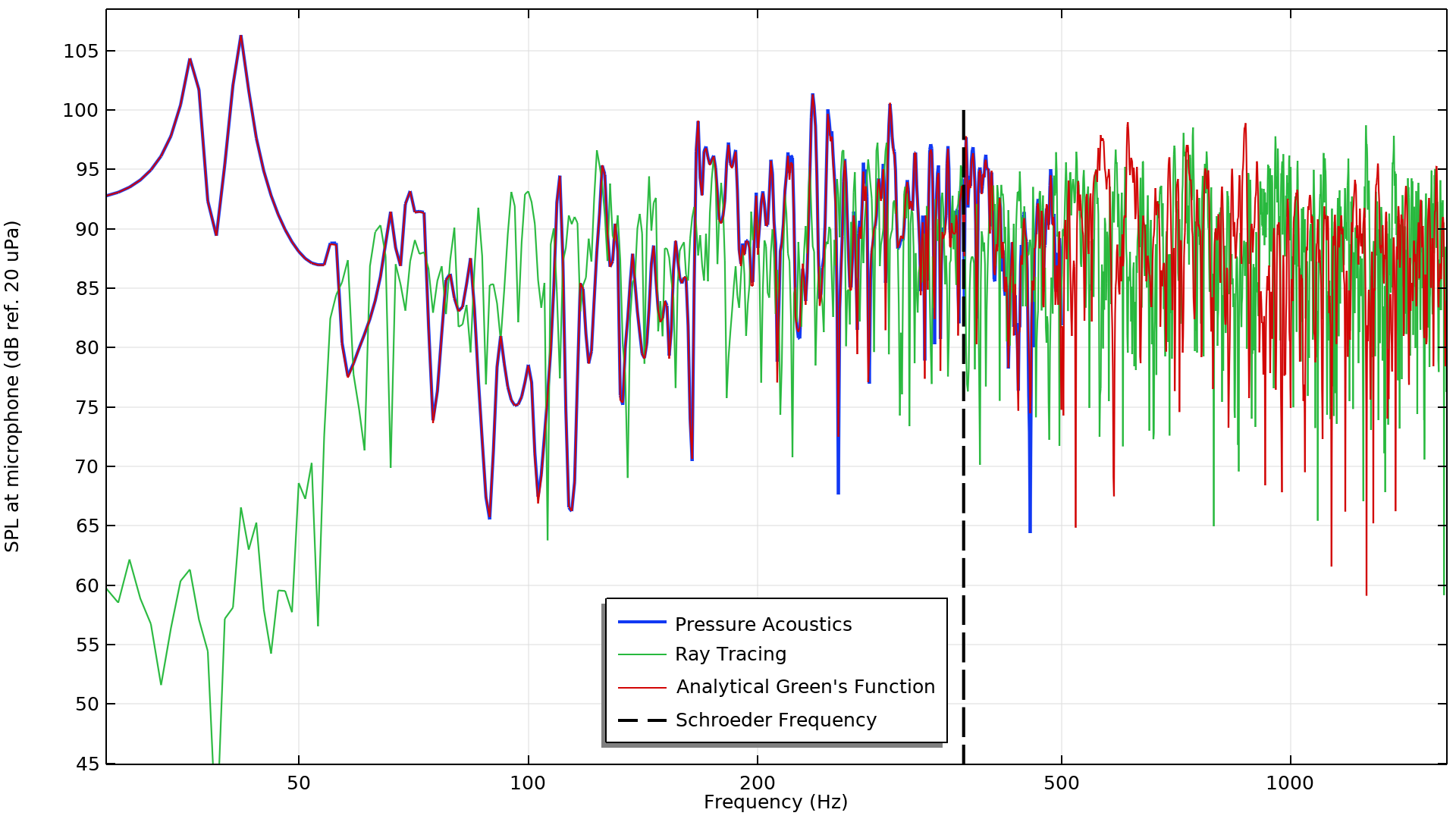
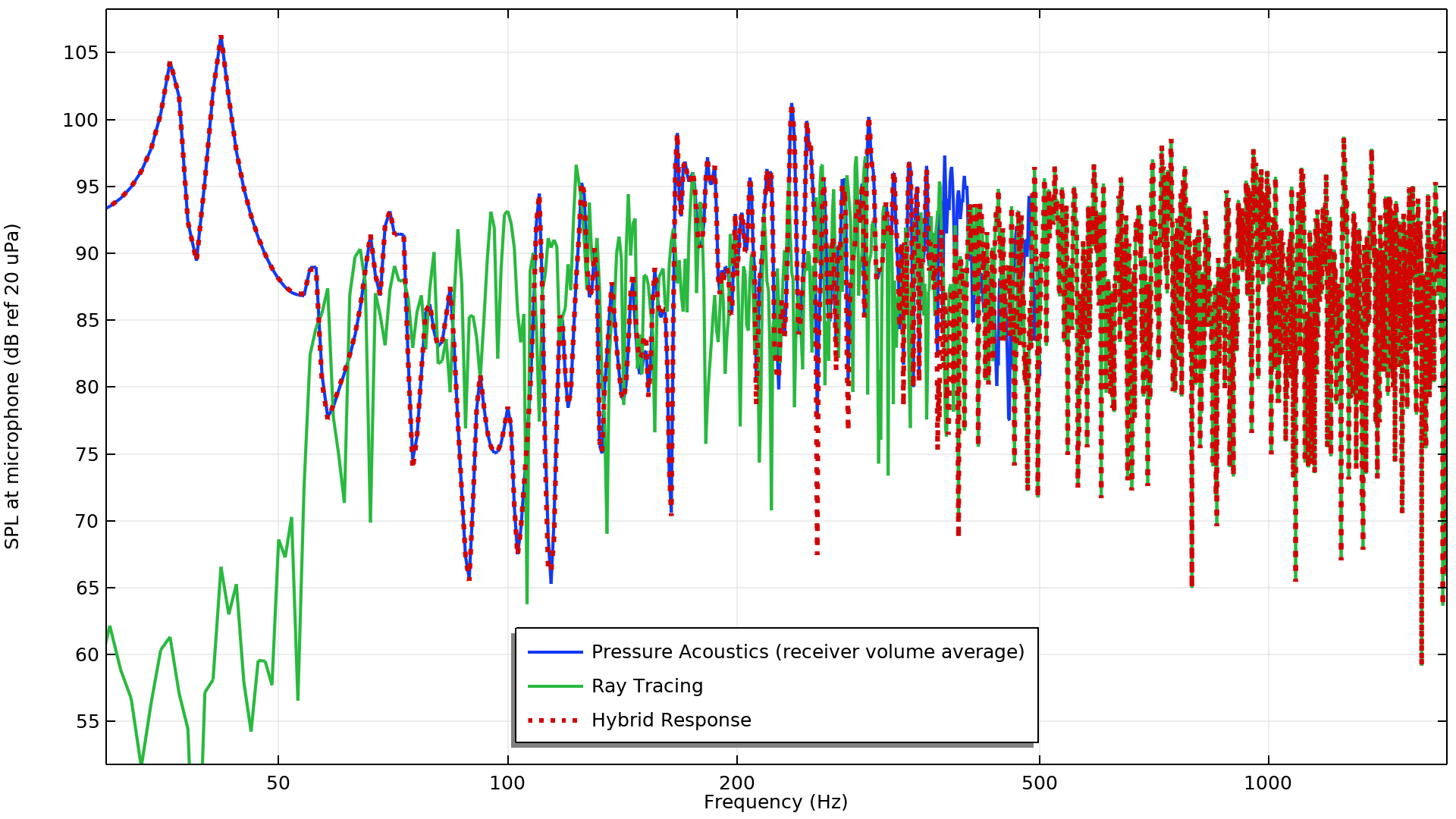
通过压力声学研究、射线追踪研究和解析的公式计算的麦克风声压级。黑色虚线表示施罗德频率。
根据这个图,我们可以得出几个关键的结论。首先,分析结果与高达 500Hz 的压力声学研究结果非常吻合,这是该研究中的最大频率。这个结果可以作为一个良好的基准,表明模型的设置是正确的。
将射线追踪结果与其他结果进行比较时,很明显低频声压级并不匹配。这些结果是意料之中的,因为射线追踪本质上不是一种基于波的方法,并且不能捕获在低频下占主导地位的模态行为。我们可以得出结论,射线追踪结果在低频下并不准确,尤其是在这个模型中当频率低于 50Hz 时。
压力声学图中的前两个共振峰对应于两种不同的模态,它们被脉冲源激发,但声能还没有被壁强烈吸收。由于我们在模型中考虑了弱吸收,因此这里的模态几乎等于具有硬声场壁的房间的模态。参考文献5推导并计算了考虑刚性边界条件的相同大小房间(4 .7m x 4.1m x 3.1m)的前 20 种模态(参见参考文献5中的表3.1)。前两种模式是 36.17Hz 的(1,0,0)模态和 41.46Hz 的(0,1,0)模态。它们分别对应于 x 方向和 y 方向上的第一种模态,并与上图中的前两个峰值保持一致。
117Hz 以下有 20 种模式,随着频率的增加,越来越多的模态会影响房间的混响行为。在低频下,模态间隔很远,并且模态的带宽也不重叠。在高频下,模态确实会重叠,这会导致嘈杂的频率响应。由于射线追踪不是一种基于波的方法,因此即使高于施罗德频率,射线追踪的结果也不会与解析结果完全一致。然而,射线追踪和解析结果都显示出与施罗德频率以上的声压级相似的特征和范围。这意味着,高于施罗德频率的射线追踪结果可用于准确估计脉冲响应,其标准是根据在输入倍频程频段上取平均值时,保持与真实信号相同的能量含量。
组合方法
我们还可以将压力声学和射线声学模型的结果组合在一起,创建宽带脉冲响应信号。与参考文献6中描述的方法类似,这可以通过采用低通滤波压力声学响应,并将其添加到高通滤波射线声学响应中来完成。这个方法利用了傅里叶变换的线性特性。
使用的滤波器类型和信号过滤位置的名称不是由任何工程标准设定的。可以根据行业具体实践或工程判断选择所实施的数字信号处理技术。这个模型通过简单的理想阶跃滤波器过滤施罗德频率以下的信号,演示了组合的概念。
信号组合的设置如下:
- 用全局常微分方程和微分代数方程 接口的零维组件
- 将射线声学 模型的结果导出到文件中,并作为插值曲线导入组件3
- 使用研究设置中的因变量值 将压力声学 模型的结果传递到研究3
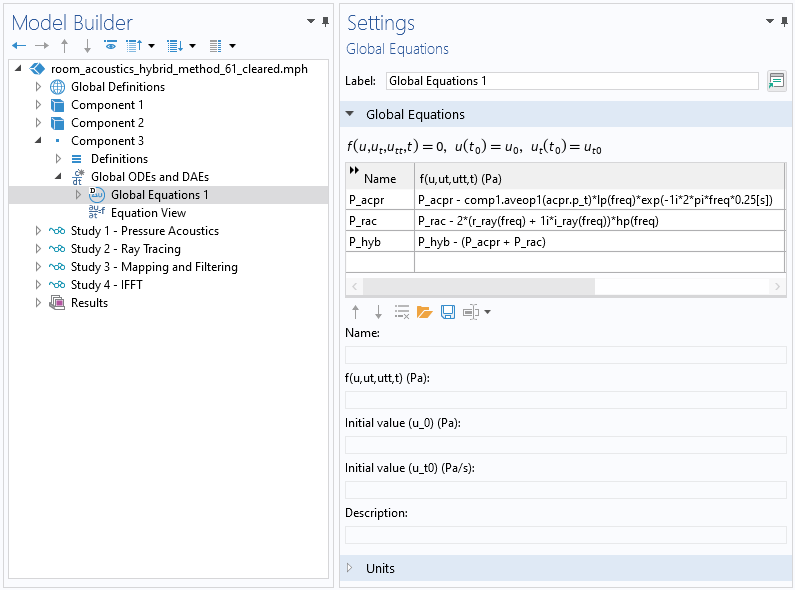
在下图中,全局方程 被添加到了组件3:
这里,P_acpr 是接收器处的体积平均压力。该表达式显示了压力经过低通滤波并随时间偏移(0.25s),以符合脉冲响应 绘图类型的惯例,方便后续进行比较。P_rac 是来自脉冲响应快速傅里叶变换(FFT)的插值函数的压力。表达式 P_rac 使用了插值函数 r_ray 和 i_ray ,即射线追踪研究(研究2)的压力的实部和虚部。通过压力表达式还可以看出射线压力通过了高通滤波并乘 2。系数为 2 是因为在研究3中仅计算了正频率,而插值是针对全频谱的。最后, P_hyb 是低通滤波压力声学响应和高通滤波射线追踪响应的总和(使用的方法与参考文献6中使用的方法类似)。
下图显示了原始信号和仅使用 组件3运行频域研究后组合信号的比较。在这幅图中,我们可以看到,压力声学和射线追踪结果的结合使混合响应具有正确的频率响应。
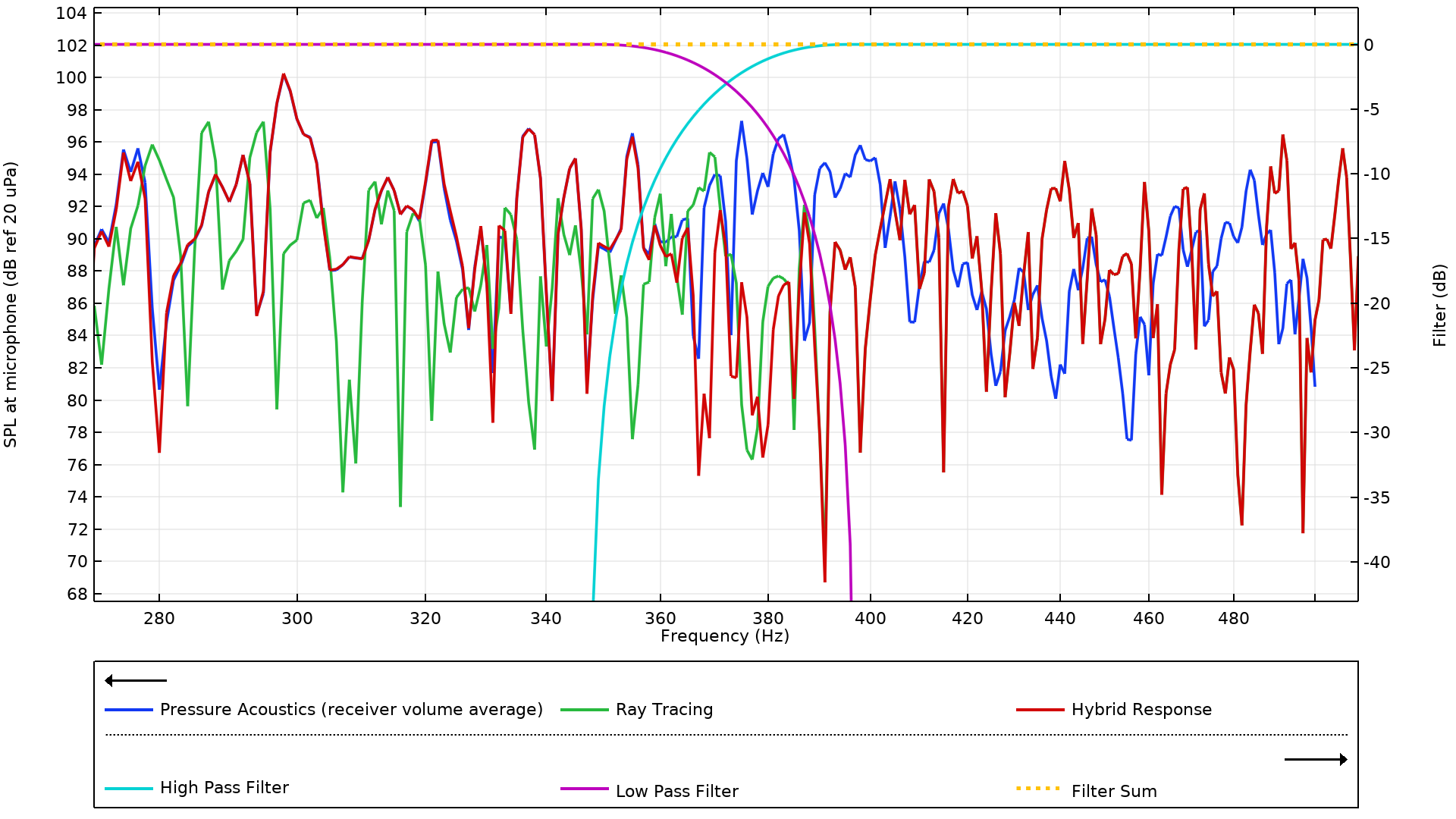
理想的滤波器是使用阶跃函数实现的,对于高通滤波器 hp(freq),从 0 步进到 1,对于低通滤波器 lp(freq),从 1 步进到 0。两个功能中都包含一个 50Hz 平滑过渡区,并将阶跃转换的位置设置为施罗德频率。将两个函数都添加到组件3 定义下。下图显示了施罗德频率附近的混合响应。从图中我们可以分析理想滤波器的特性。值得注意的是,理想滤波器在施罗德频率下的增益因数均为 -3dB,这意味着这里的响应是两者的平均值。在其他地方,混合响应是两种响应的加权组合,具体取决于频率。滤波器的总和在所有频率上都是 0dB。
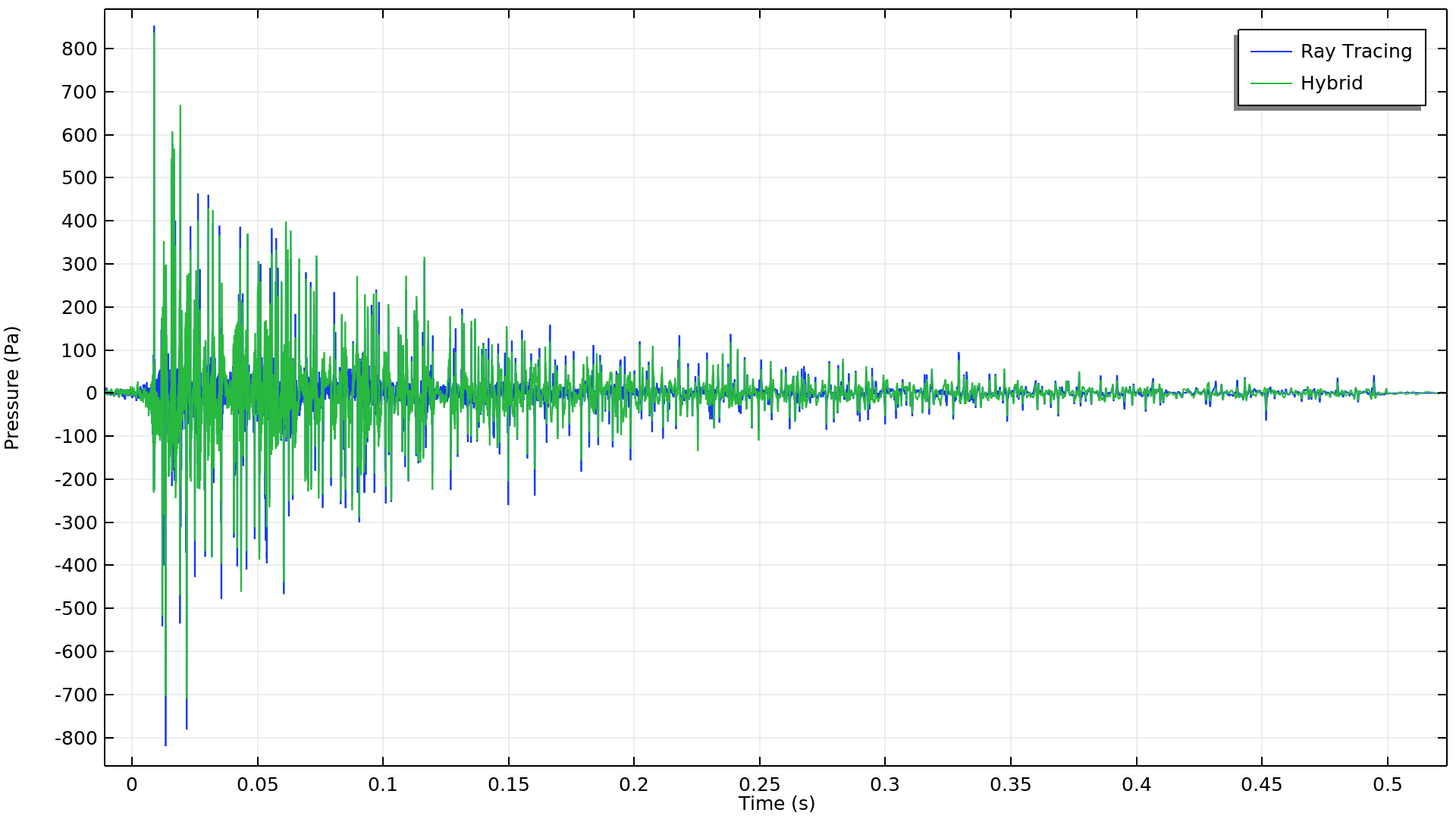
为了从频率分析返回时域分析,我们运行第四个也是最后一个研究,包括一个从频域时间域的 FFT 步骤。在这个步骤中,Tukey 窗口函数用于对逆 FFT(IFFT)进行带限制。混合信号和原始射线追踪信号的比较如下图所示。虽然我们在时域中可以看到一些差异,但通过直接查看频谱更容易发现差异。很明显,在全部频率范围内,这里计算的混合压力与时间信号比纯射线追踪信号更准确。这种精度意味着混合信号可用于计算其他室内声学指标,例如清晰度、混响时间或语音传输指数,或导出用于房间听觉化的外部分析工具。
动手尝试
这篇文章,我们介绍了一种将射线追踪和有限元方法组合使用来获得宽带脉冲响应的方法。文中显示的所有模拟都是在 COMSOL Multiphysics 中完成的,并且解被集成到单个模型中。这个方法对于在高频下使用全波方法可能并不总是可行,但对于大型室内声学仿真特别有用。单击下面的按钮,尝试自己动手,您可以从 COMSOL 案例库中下载该模型文件:
更多资源
如果您想了解更多室内声学模型,可以在 COMSOL 案例库中查看以下相关模型:
- 室内音乐厅:通过射线追踪模拟柏林音乐厅小礼堂的声学效果。
- 轿车内部声学模型 – 频域分析: 使用压力声学对轿车内部声学进行建模。迭代求解器用于求解高达 4kHz 的模型。
参考文献
- Morse, Philip McCord, and K. Uno Ingard. Theoretical Acoustics. Princeton University Press, 1986.
- Okoyenta, Augustus R., et al. “A Short Survey on Green’s Function for Acoustic Problems.” Journal of Theoretical and Computational Acoustics 28.02 (2020): 1950025.
- M. R. Schroeder, New Method of Measuring Reverberation Time, J. Acoust. Soc. Am., 37 (1965).
- M. R. Schroeder, Integrated-Impulse method measuring sound decay without using impulses, J. Acoust. Soc. Am., 66 (1979).
- Kuttruff, Heinrich. Room Acoustics. CRC Press, 2016.
- Aretz, Marc, et al. “Combined broadband impulse responses using FEM and hybrid ray-based methods.” EAA Symposium on Auralization, 2009.






评论 (8)
崎 杨
2023-04-11你好,我在计算的时候只改变了声源和麦克风的位置,同态计算的结果高频部分与射线声学计算的结果无法重合,并且声源和接受位置的改变并没有对同态计算结果产生影响,请问这是为什么那?
Hao Li
2023-04-20 COMSOL 员工您好!
这里不清楚您指的“同态计算”是什么含义,您可以将您的问题描述清楚并上传模型到Support系统,以帮助我们给您提供具体的建议。
感谢您的评论。
如果有进一步问题,建议您联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
磊 阳
2023-07-24您好,我想知道射线声学中怎么设置壁面可以让射线带一定损失穿过(具有一定隔声)并且有反射,而不是完全穿过或者只有反射
Yuxin Xu
2024-06-03您好!我想请问是否能够实现射线声学声源时域信号自定义?
Hao Li
2024-06-05 COMSOL 员工您好!
感谢您的评论。
可以定义射线声学声源的指向性等信息,具体可参考案例
https://cn.comsol.com/model/room-impulse-response-of-a-smart-speaker-115561
https://cn.comsol.com/model/small-concert-hall-acoustics-20145
如果有进一步问题,建议您联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
Wxs
2024-07-08您好,请问声源的脉冲信号形式怎么设置?
Hao Li
2024-07-10 COMSOL 员工射线声学中单次释放声粒子的过程就可以视为脉冲信号。普通有限元中可以在瞬态定义,如平面波辐射下的入射波条件,可以直接选择脉冲信号,输入频率及时间即可定义。
NA JIN
2026-01-23计算速度太慢了,不是很方便,不如导出数据单独处理