
我们可以通过各类介质薄膜工具控制光的传播。例如,它们可以用作抗反射涂层来减少系统内的杂散光;还可以作为低损耗的反射器或滤波器使用,实现对特定频率辐射的选择性传输。今天的博客将介绍射线光学模块的部分内置功能,可用于模拟包含介质膜的光学系统。
理解薄膜与透射率
由于介质薄膜的光学属性基于多个表面的反射与折射,我们将从查看材料非连续性边界处的反射与折射控制方程开始,即两种介质交界处的边界。光在边界处的反射与折射由 Fresnel 方程组控制:
(1)
t_s &= \frac{2n_1 \cos\theta_i}{n_1 \cos\theta_i+n_2 \cos\theta_t} \\
t_p &= \frac{2n_1 \cos\theta_i}{n_2 \cos\theta_i+n_1 \cos\theta_t} \\
r_s &= \frac{n_1 \cos\theta_i-n_2 \cos\theta_t}{n_1 \cos\theta_i+n_2 \cos\theta_t} \\
r_p &= \frac{n_2 \cos\theta_i-n_1 \cos\theta_t}{n_2 \cos\theta_i+n_1 \cos\theta_t}
\end{aligned}
其中 n_1 和 n_2 分别是包含入射光线和折射光线的相邻域中的折射率,\theta_i 是入射角,\theta_t 是折射角,如下图所示。

系数 r 和 t 分别是反射和透射系数。下标 s 和 p 显示了入射光线的偏振。如果电场矢量垂直于入射面(即包括入射光线及面法向的面),则光线为 s 偏振;如果电场矢量位于入射面内,则光线为 p 偏振。
为清楚起见,我们在下方的讨论中省去了用于说明 s 偏振及 p 偏振的后缀,并假定使用了正确的反射和透射系数。
如果入射光线的强度为 I_0,反射及折射光线的强度则为
(2)
I_r &= R I_0 \\
I_t &= T I_0 \\
R &= \left|r\right|^2 \\
T &= \frac{n_2 \cos\theta_t}{n_1 \cos\theta_i}\left|t\right|^2
\end{aligned}
我们将物理量 R 和 T 分别称作反射率和透射率。通过结合方程 (2) 与方程 (1) 中的任意一组 Fresnel 系数,我们观察到能量守恒,I_r+I_t=I_0。
我们现在将考察光线在两个间距较小的平行边界间发生反射及折射的情况。这两个边界构成了用于分隔两种介质的介质薄膜表面。这里的“小”通常是指膜厚度与电磁波长的量级相当。假设膜厚度远小于辐射的相干长度,也就是说,它的长度尺度与膜厚度相当,那我们就可以将电磁波作为完美正弦曲线处理。我们希望计算传播至薄膜两侧域中的辐射强度。
如下图所示,我们可以想象入射至折射率为 n_2 的狭窄区域的单独一条光线,该区域夹于折射率为 n_1 和 n_3 的两种介质之间。域 1 及域 2 界面的反射系数设为 r_{12},域 2 及域 3 之间边界的反射系数为 r_{23}。
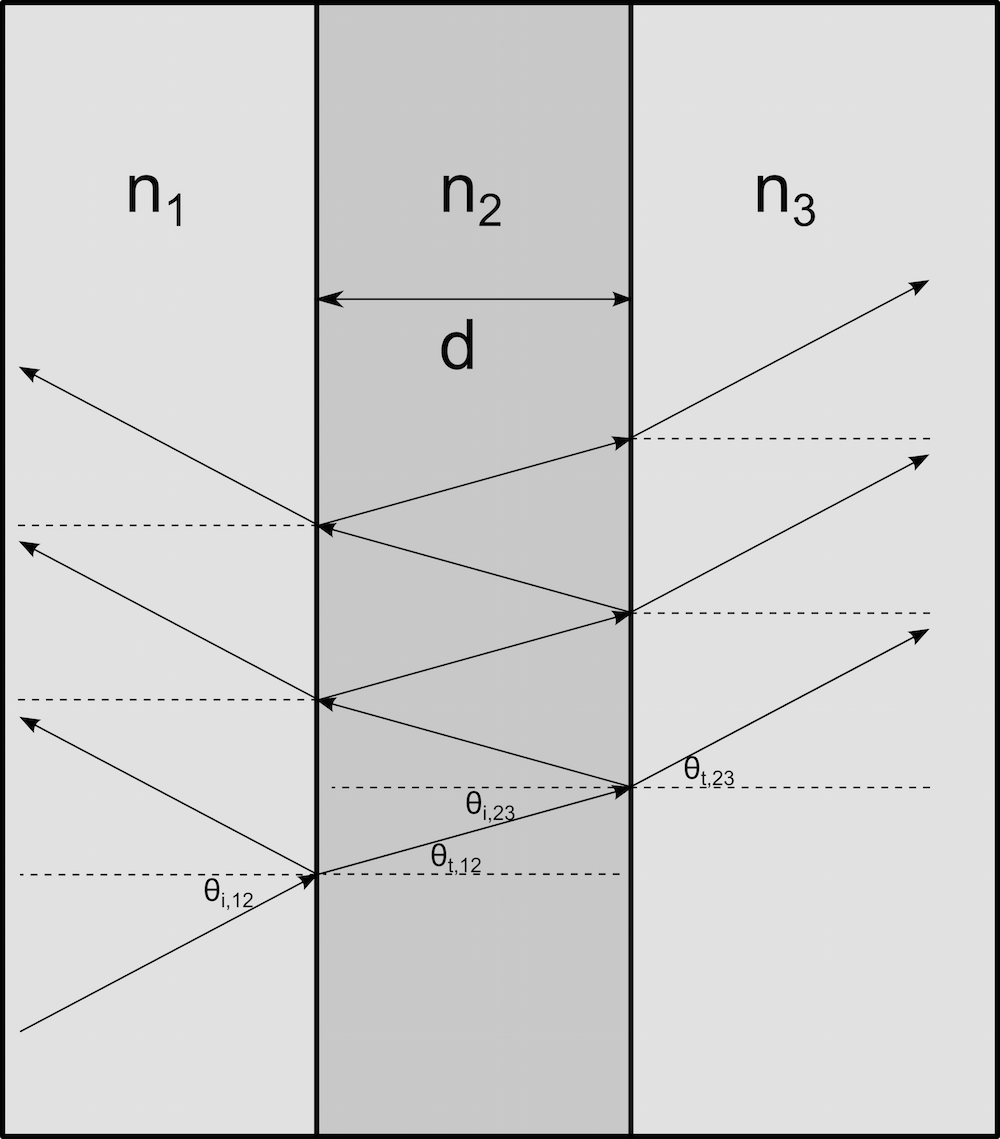
光线会在进入薄膜后在两条边界之间来回反射。每次光线到达相邻域的边界时,都会向该域折射入一条光线,造成膜内强度的降低。传播至薄膜相邻域中的多条光线的幅值,将对总的反射和透射场产生贡献。由于每条光线在膜内的传输距离不同,相互之间可能发生相长或相消干涉,换言之,透射及反射场的总幅值可能增加或降低,具体取决于光线间的相位差。
由于这些干涉效应,反射及折射辐射的强度将依赖于自由空间波长 \lambda_0 与膜厚度 d 之间的比值,而不仅是介质属性与入射角。根据《Optical Properties of Thin Solid Films》(O. S. Heavens, 1991),单层膜的等效反射系数 req 可通过以下公式得到
(3)
其中 \delta 是由于穿过膜造成的相位延迟:
(4)
其中 \theta_2 是光线穿过薄膜时与面法向之间的锐角。如果将多个薄层并排放置,我们将能通过方程 (3) 对整个结构的透射率和反射率执行递归计算。我们还可以通过其他算法计算多层膜的透射率和反射率,比如《Optical Properties of Thin Solid Films》(O. S. Heavens, 1991)和《Principles of Optics》(M. Born 与 E. Wolf,1999) 中的介绍。
抗反射涂层
我们发现,在薄膜两侧电磁波干涉的影响下,膜的透射率会明显高于或低于两介质间单条边界的透射率,具体取决于介质属性、膜厚度、波长及入射角。我们可以通过该行为来控制光学系统内透射或反射的辐射量。
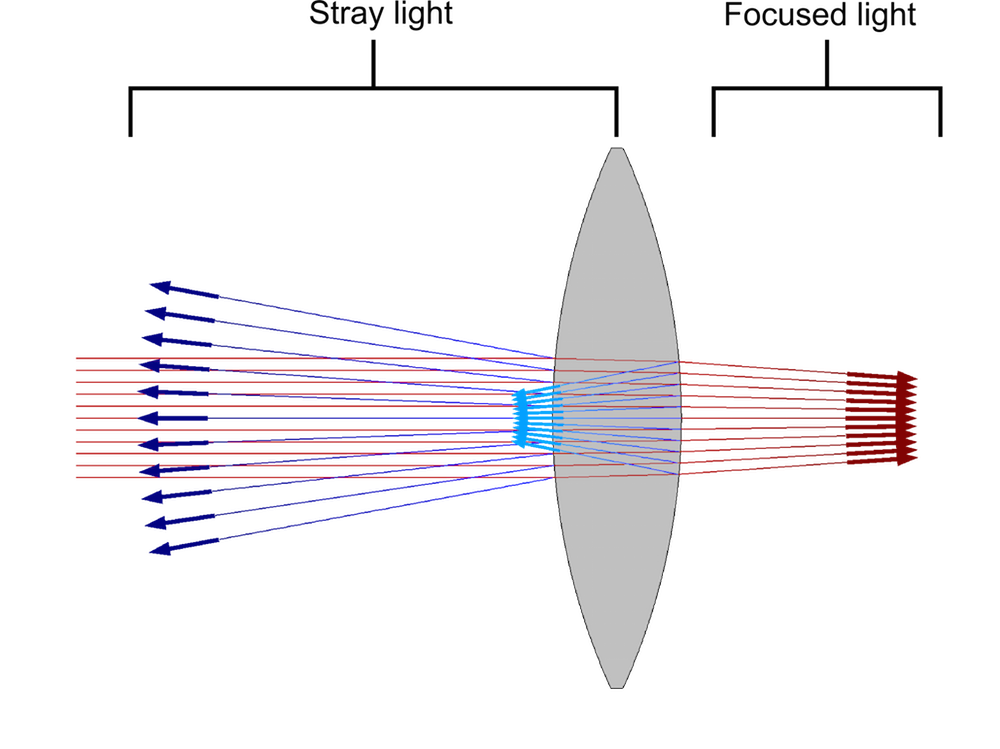
当使用介电薄膜来降低材料非连续处的反射率时,这类薄膜会形成一个抗反射涂层。涂层可以是单层或多层。抗反射涂层可以显著降低光学系统中多余或我们不希望的辐射量,也称杂散光。例如,假设通过折射率为 1.45 的玻璃透镜来聚焦传播通过室内的光线;假定入射角接近零,那么玻璃表面的反射率是
(5)
也就是说,超过 3% 的辐射将在到达透镜时直接被反射掉,这减少了可通过透镜进行恰当聚焦的光线数量。我们通常希望尽可能减少少杂散光。
例如,如果膜两侧的反射系数相同,r_{12}=r_{23},光线穿过层的相位延迟为 \delta = \pi/2,那我们将能通过方程 (3) 得到 r_{\textrm{eq}}=0,没有任何辐射被反射掉。对于法向入射的光线,我们可以通过调整层厚度使 d=\lambda_0/(4n_2),得到期望的相位延迟,例如将单层涂层的光学厚度设为波长的 1/4。为了使 r_{12}=r_{23},膜的折射率应为两侧折射率的几何平均值,即 n_2=\sqrt{n_1 n_3}。
对于上文提到的单层涂层,它在特定辐射频率及入射角下的反射率恰好为零。此外,我们也许无法找到一种折射率等于薄膜两侧折射率几何平均值的材料。解决方案之一是使用反射率能在较宽频率下保持较低的多层膜,这还能增强材料选择的灵活度。
射线光学模块包括多项可在表面应用单层或多层膜的设定;包括可在边界处应用单层抗反射涂层的内置选项;以及针对特定折射率、电磁波长和入射角应用含指定反射率或透射率的单层膜的内置设定;此外,还可以通过直接指定每层的折射率和厚度,在边界处应用单层或多层膜。
例如,下图对比了两层抗反射涂层(每层厚度均为 1/4 波长)以及三层抗反射涂层(各层厚度分别为 1/4 波长、1/2 波长和 1/4波长)的反射率。我们看到 1/4-1/4 膜可以在大约 100 nm 的范围内提供小于 0.5%的反射率,而 1/4-1/2-1/4 膜则能在超过 250 nm 的范围提供小于 0.5% 的反射率。
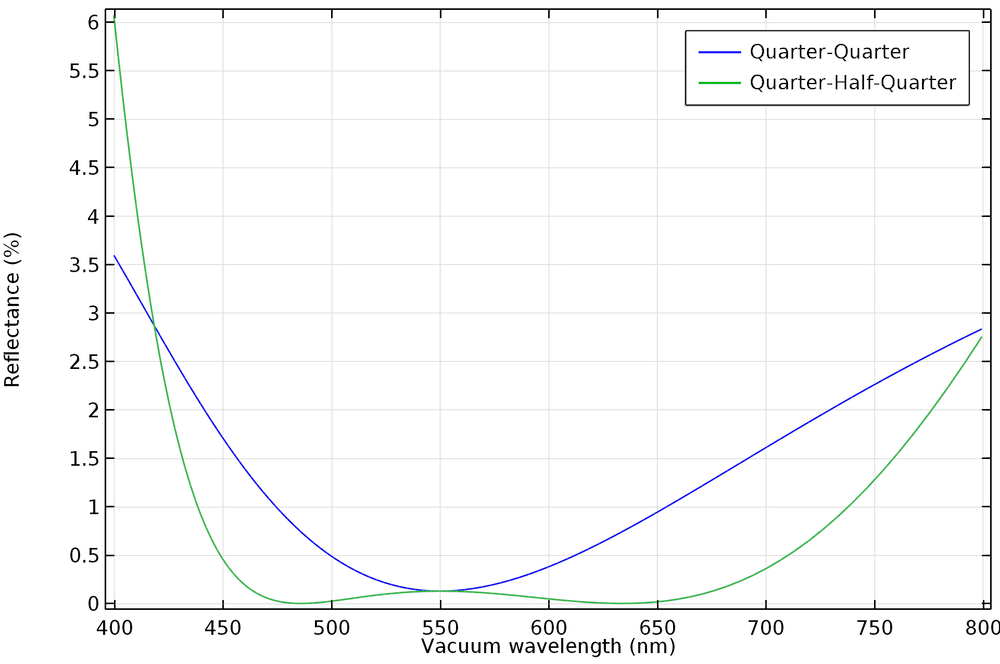
如希望了解有关介电膜设定的详细信息,请阅读抗反射涂层,多层教程。
高反射涂层
我们也可以使用介质薄膜来增大边界处的反射率,创建一个损耗明显低于闪亮金属表面的镜面。我们将此类膜配置称为高反射涂层或分布式 Bragg 反射器 (DBR)。DBR 包括交错放置的较高折射率 (n_H) 层和较低折射率 (n_L) 层 ,如下图所示。
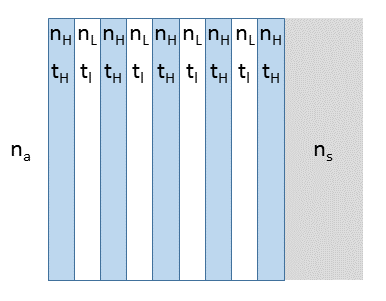
层厚度由以下方程确定
(6)
DBR 由光子禁带 \Delta \lambda_0 表征,即反射率接近 1 的波长范围:
(7)
随着层数的增加,反射率在禁带内将越接近 1。
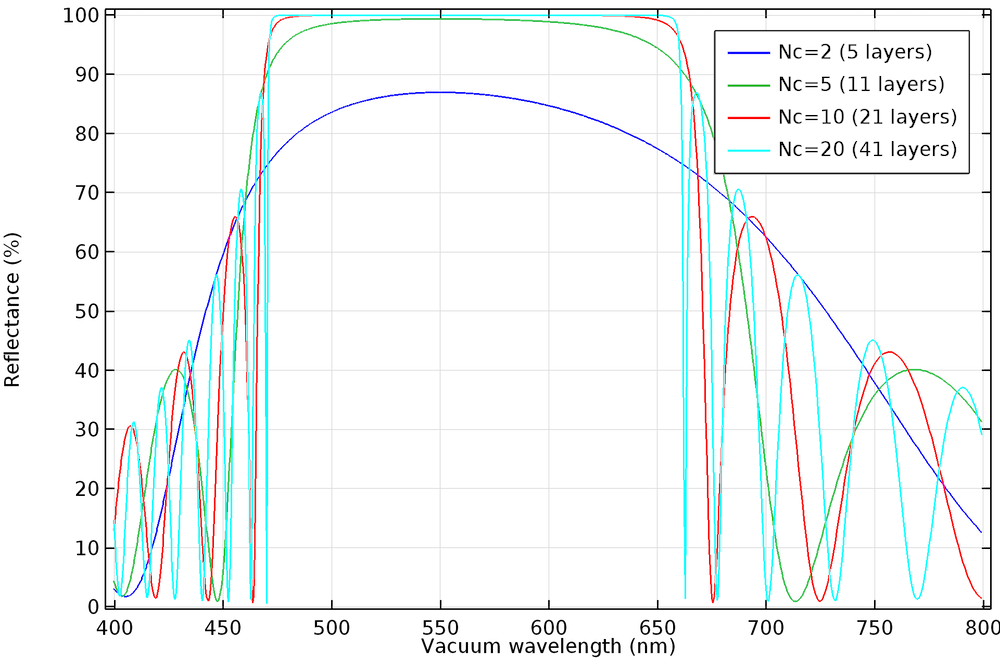
如希望了解分布式 Bragg 反射器的详细设定,您可查看“分布式 Bragg 反射器”教程。
教程还包括了可直接运行的 App。利用分布式 Bragg 反射器 (DBR) 滤波器 App,您可以计算较宽频率范围内的 DBR 反射率。除了以真空波长函数的形式绘制反射率,该 App 还将计算禁带(反射率超过指定阈值的区域)的宽度。
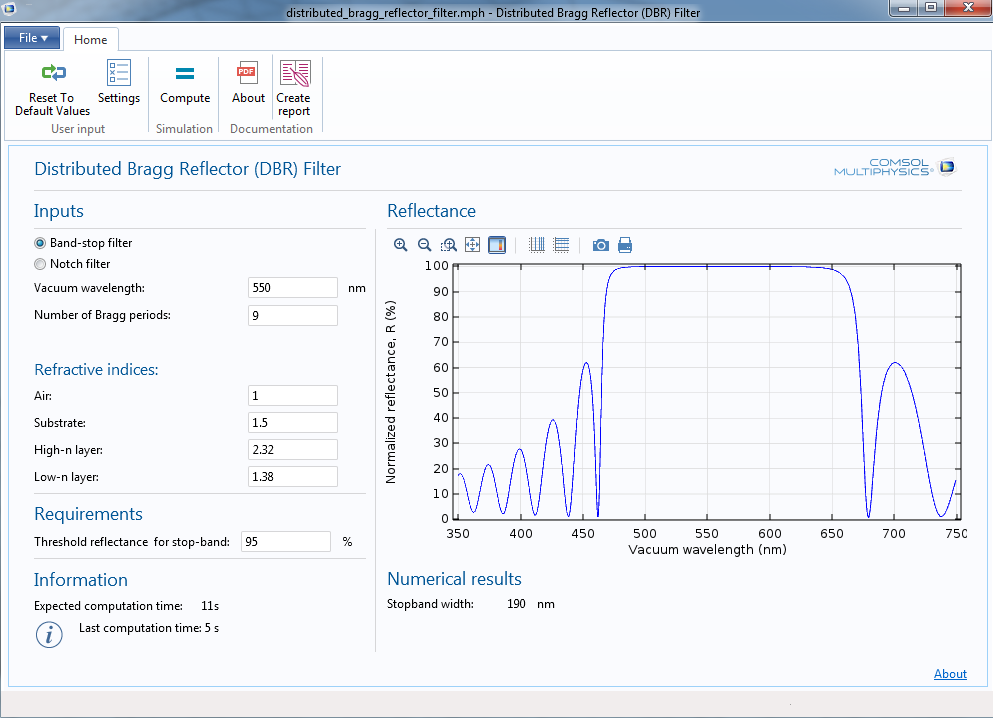
如前所述,典型 DRB 中每层的光学厚度等于 \lambda_0/4。如果在 DBR 中插入光学厚度为 \lambda_0/2 的一层,就可以将辐射传输至禁带中的特定频率内,如下图所示。
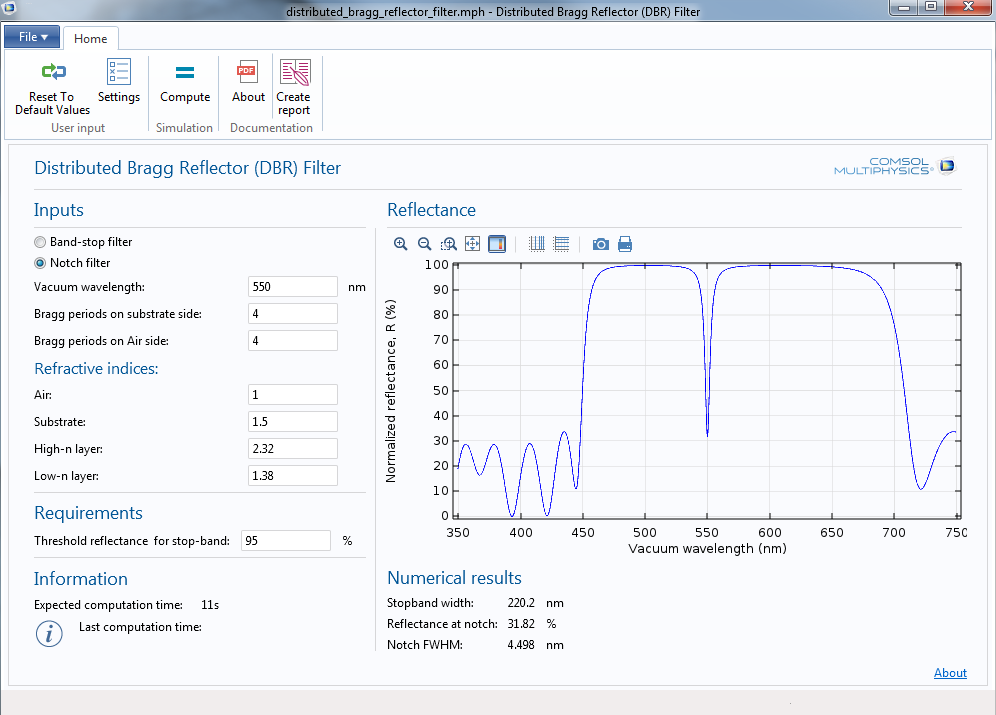
这类滤波器特别适用于从窄谱源内传输辐射,并能阻止来自其他源的污染。
您可以点击下载分布式 Bragg 反射器 (DBR) 滤波器 App。
拓展阅读
- 我们在 2015 年 4 月 15 日发布了 COMSOL Multiphysics 5.1 版本,您可在此页面浏览该版本对射线光学模块进行的更新。



评论 (0)