最新内容

封闭腔体积的求解和控制
在 COMSOL® 软件中,有多种方法可以模拟流体与固体的相互作用。例如,可以使用完整的纳维-斯托克斯方程对压力场和流体速度场进行显式建模。尽管这种方法非常准确,但对于一些流-固耦合问题来说,它的计算成本比实际需要的要高得多。今天这篇文章,我们将介绍一种模拟包含不可压缩流体的封闭腔的方法,假设通过流体的动量和能量传递很小。 编者注: 作者撰写这篇博客的时候,COMSOL 中还没有计算封闭腔中流体载荷的功能。现在,COMSOL Multiphysics® 6.2 版本新增了封闭腔功能,可用于计算封闭腔中的流体载荷。 模拟封闭腔中的流体 我们来看一个 COMSOL 案例库中的示例:超弹性密封条的压缩模型。这个示例考虑的是压缩的软橡胶密封件的横截面。腔体中封闭的流体是空气。该示例计算了压缩力,并将密封件中考虑压缩空气影响与不考虑压缩空气影响的结果进行了比较。 软橡胶密封件的压缩模型。仿真结果显示了应力和应变。使用了不同的方法对密封件内部的空气进行模拟。 示例模型将空气视为可压缩流体,计算了随此二维示例中密封件的横截面积 A 变化的腔体内部压力 p 的变化。接下来,让我们来看看它是如何实现的。将腔体内的空气视为绝热压缩下的理想气体,则压力-密度关系为: \frac{p} {p0}=\left(\frac{\rho} {\rho0} \right)^\gamma=\left(\frac{A0} {A}\right)^\gamma 所以,要计算压力的变化,只需要知道面积的变化就可以了。假设未压缩密封件的面积和压力,以及比热率 \gamma均已知,如何计算横截面积呢?该面积由一个我们甚至不想考虑在模型中的区域来描述。使用高斯定理将面积积分转换为边界积分: A=\int\Omega 1 d\Omega = \int\Omega \left( \nabla \cdot \left[ \begin {array} {c} x \ 0 \end {array} \right]\right) d\Omega = \oint x nx d\Gamma 其中,x 是变形的密封件构型的 x 坐标,n_x 是边界的向外法向量的 x 分量,也在变形配置中,由此给定密封件的封闭区域。这是通过一个定义在封闭体积的完整内部边界上,名为 AreaInt 的积分耦合算子 完成的。变形区域由在“完整模型”上定义的变量 EnclosedArea 定义。 在密封件的内边界上定义面积积分。 分别定义封闭面积和内部压力的变量的定义。必须使用负号来计算面积,因为固体的法线指向腔体。 计算出的变形面积用于确定密封件变形时内部压力的变化。计算得出的压差作为一个载荷施加到密封件内部。要查看上述方法的完整操作,请查看超弹性密封条模型文档。 考虑不可压缩流体 上述方法假设流体是可压缩的,并且密封件的内部压力与面积变化呈函数关系。但如果流体是不可压缩的呢?假设考虑的不是包含可压缩空气的密封件,而是一个充满水的气囊,其中水几乎是不可压缩的。那么,随着结构的变形,封闭的面积不能改变,上述方法就行不通了。因此,我们需要一个替代方案。 我们将 全局方程 功能添加到固体力学接口,通过在这个模型中引入一个额外的方程来求解流体内的压力,使体积不会发生变化。我们来看看这个接口: 引入的全局方程的设置。需要启用高级物理选项才能查看此功能。 上面的屏幕截图显示了用于额外变量 压力 的 全局方程 设置。此方程成立的条件是变量 封闭区域 等于初始面积 123.63 […]

COMSOL Multiphysics 中自由剖分四面体网格的尺寸参数
对几何进行网格剖分是仿真过程的重要组成部分,它对于最快地得到最好的结果至关重要。不过,没人希望因要找出最佳的网格规格而影响进度。为了帮助解决该问题,COMSOL Multiphysics 内置了 9 种网格剖分尺寸参数。这里,我们将介绍自由剖分四面体网格的尺寸参数。在后续的博客中,我们还将介绍棱柱、六面体单元和其他类型的扫略网格剖分。

空间与时间的积分方法概述
积分是数学模型中最重要的功能之一,特别是对数值仿真而言。例如,偏微分方程组 (PDEs) 就是由积分平衡方程派生而来。当需要对偏微分方程进行数值求解时,积分也将发挥非常重要的作用。本篇博客介绍了 COMSOL 软件中可用的积分方法,以及如何使用,供您参考。
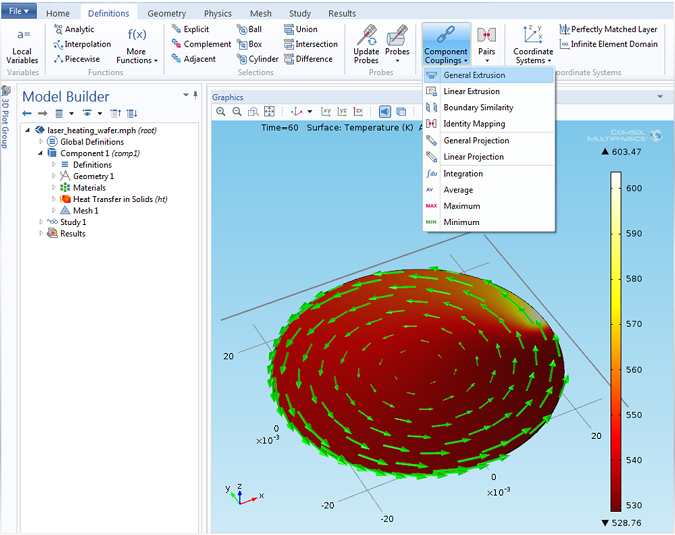
在 COMSOL 中使用广义拉伸耦合算子:动态探测
请看一个激光加热的例子,热源(激光)在移动,几何体也在移动。如何使用广义拉伸耦合算子在几何体的某一点上探测解?

利用混合并行计算技术加速物理场仿真
二十年前,配备了多达 1000 个处理单元的向量处理器超级计算机在超级计算机 500 强中占据了统治地位。随着时间推移,大规模并行计算集群不仅迅速取代了向量超级计算机成为了榜单中的新霸主,同时还促使了分布式计算的兴起。集群的每个计算节点上最初只有一个专用于高性能计算的单核处理器,很快,人们针对需要共享内存的节点,增加节点上的处理器数量,并以这种具备内存共享能力的并行计算机为基础,开发出了多核处理器,满足了各类计算应用对高效算法的需求。再看今天的超级计算机 500 强排名,我们会发现当中大多数集群均由数量众多的计算节点组成,每个节点又包含多个插槽(socket),每个插槽连接着最多可达八核的多核处理器。并行计算是一种适用于共享内存计算系统的技术,与基于分布式内存的集群采用的并行计算技术全然不同。为了实现高效率的并行计算,我们需要一种两者并用(混合)的机制。

模拟电磁波和周期性结构
我们经常想要模拟入射到周期性结构中的电磁波(光、微波),例如衍射光栅、超材料,或频率选择表面。这可以使用 COMSOL 产品库中的 RF 或波动光学模块来完成。两个模块都提供了 Floquet 周期性边界条件和周期性端口,并将反射和透射衍射级作为入射角和波长的函数进行计算。本博客将介绍这类分析背后的概念,并将介绍这类问题的设定方法。
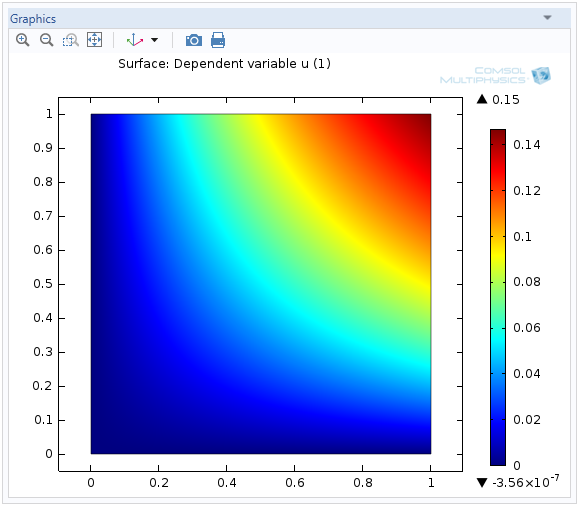
求解代数场方程
COMSOL Multiphysics® 通常用于求解 PDE,ODE 和初始值问题。但是,您是否知道它也可求以解决代数方程,甚至超越方程?
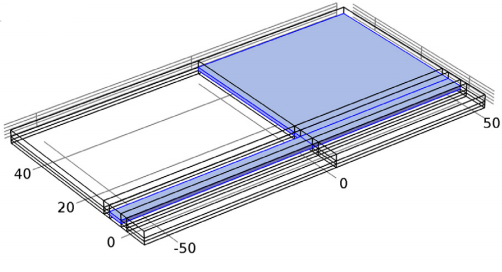
使用 COMSOL 模拟 RF MEMS 开关
RF MEMS 开关通常由微机械桥或悬臂、衬底和电极或介电层组成。您可以使用 RF 仿真来设计这样的器件。



