COMSOL 博客

微波等离子体的原理和仿真方法

作者 Daniel Smith

2013年 12月 11日

微波等离子体，或称波加热放电，在半导体加工、表面处理和有害气体排放等许多工业领域都有应用。这篇博客介绍了 COMSOL 等离子体模块中的微波等离子体 接口的理论基础。

简介

当电子从穿透等离子体的电磁波中获得足够的能量，微波等离子体就会持续放电。微波等离子体的物理特性有很大不同，具体取决于传播的是 TE 模式（面外电场）还是 TM 模式（面内电场）。在这两种情况下，电磁波都不可能穿透到电子密度超过临界电子密度的等离子体区域（2.45GHz 时约为 7.6×10¹⁶ 1/m³）。临界电子密度由下列公式计算：

n_e = \frac{\epsilon_0 m_e \omega^2} {e^2}

式中，\epsilon_0 是自由空间的介电常数，m_e 是电子质量，\omega 是角频率，e 是电子电荷。这个临界值对应于电磁波的角频率与等离子体频率相等的点。微波等离子体的压力范围非常宽。对于电子回旋共振等离子体，压力可以在 1Pa 左右，而对于非电子回旋共振等离子体，压力范围通常在 100Pa 到一个大气压之间。功率在几瓦到几千瓦不等。由于微波电源很便宜，所以微波等离子体很受欢迎。

微波放电理论

为了理解与微波等离子体仿真有关的细微差别，有必要复习一下如何维持放电的理论。微波在时间尺度上的等离子体特性与较长期的等离子体行为是不同的，后者受双极场的约束。

电磁场

在等离子体模块中，电磁波在频域中计算，所有其他变量在时域中计算。为了证明这种方法的合理性，我们从麦克斯韦方程开始：

(2)

\nabla \times \mathbf{\tilde{E}} = -\frac{\partial \mathbf{\tilde{B}}}{\partial t}

(3)

\nabla \times \mathbf{\tilde{H}} =\mathbf{\tilde{J}}_p+\frac{\partial \mathbf{\tilde{D}}} {\partial t}

式中，\mathbf{\tilde{E}} 是电场（V/m），\mathbf{\tilde{B}} 是磁通密度（T），\mathbf{\tilde{H}} 是磁场（A/m），\mathbf{\tilde{J}_p} 是等离子体电流密度（A/m² ），\mathbf{\tilde{D}} 是电位移（C/m² ）。波浪号用于表示场随频率 \omega/2 \pi 在时间上变化。等离子体电流密度可以用下列表达式来近似计算：

(4)

\mathbf{\tilde{J}}_p = -e n_e \mathbf{\tilde{v}_e}

式中，e 是单位电荷（C），n_e 是电子密度（1/m³），\mathbf{\tilde{v}_e} 是以下两个假设下的平均电子速度（参考文献1）：

相对于微波时间尺度上的电子运动，离子运动被忽略了。
在微波时间尺度上，假定电子密度在空间上是恒定的。

微波时间尺度上的平均电子速度 \tilde{\mathbf{v}}_e，通过假设麦克斯韦分布函数和取波尔兹曼方程的第一项得到（参考文献2）：

(5)

\frac{\partial \mathbf{\tilde{v}_e}}{\partial t} = -\frac{e}{m_e}\mathbf{\tilde{E}}-\nu_m \mathbf{\tilde{v}}_e

式中，m_e 是电子质量（kg），\nu_m 是电子和背景气体之间的动量传递频率（1/s）。正如参考文献1中所指出的，这些方程是线性的，因此我们可以对方程组进行傅里叶变换。对方程(5)进行傅里叶变换，可以得到：

(6)

j \omega \mathbf{\bar{v}}_e+\nu_m \mathbf{\bar{v}}_e =-\frac{e}{m_e} \mathbf{\bar{E}}

其中波浪号已经被横线取代，现在指的是场的幅值。两边都乘以 -e n_e，然后重新排列，就可以得到：

(7)

-e n_e \mathbf{\bar{v}}_e = \frac{n_e e^2}{m_e(\nu_m + j \omega)} \mathbf{\bar{E}}

或者，用更简单的形式表示：

(8)

\mathbf{\bar{J}}_p = \sigma \mathbf{\bar{E}}

其中，

(9)

\sigma = \frac{n_e e^2}{m_e(\nu_m + j \omega)}

方程(1)和(2)可以通过对方程(2)求时间导数进行重新排列，然后代入方程(1)，得到

(10)

\nabla \times \mu^{-1} \nabla \times \mathbf{\bar{E}} = (\omega^2 \epsilon_0 \epsilon_r-j \omega \sigma)\mathbf{\bar{E}}

式中，\mu 是磁导率，\sigma 由方程(8)给出，等离子体的相对介电常数设为 1。该方程也可以在相对介电常数为复值，等离子体电导率为零（参考文献3）时进行重新表述。整个等离子体模块采用的约定是，等离子体电导率由方程(8)给出，等离子体相对介电常数被设置为1。

用适当的边界条件求解上述方程，就可以计算出从电磁场转移到电子的功率：

(11)

Q_{rh} = \frac{1}{2} \textrm{Re}(\mathbf{\bar{J}} \cdot \mathbf{\bar{E}}^*)

式中，\mathbf{\bar{J}} 是总电流密度（等离子体电流加上位移电流密度），* 表示复共轭。

双极电场

除了上述方程外，还在时域内求解了一组电子密度 n_e、电子能量密度 n_{\epsilon}、等离子体电势 V 以及所有离子和中性物质的方程。对于电子密度：

(12)

\frac{\partial n_e}{\partial t}
+ \nabla \cdot \mathbf{\Gamma}_e = R_e

其中电子通量，\mathbf{\Gamma}_e（1/(m² s)）由下式给出：

(13)

\mathbf{\Gamma}_e = -\mu_e n_e \mathbf{E}-\nabla D_e n_e

式中，\mu_e 是电子迁移率（m²/（V-s）），D_e 是电子扩散系数（m²/s）。请注意，上面给出的 \mathbf{E}，并没有与之关联的波浪号。这种情况下的电场是由于等离子体中的离子和电子分离而产生的静电场。这通常被称为双极场，并导致在比微波时间尺度长得多的时间内（微秒而不是亚纳秒）到反应堆壁上的电子和离子损失。电子能量密度 n_{\epsilon} ，用一个类似的方程计算出来：

(14)

\frac{\partial n_{\epsilon}}{\partial t} + \nabla \cdot \mathbf{\Gamma}_{\epsilon} + \mathbf{E} \cdot \mathbf{\Gamma_e} = S_{\epsilon}+ Q_{rh}/e

式中，左手边的第三项代表电子的加热或冷却，取决于它们的漂移速度是否与双极电场一致。由微波引起的电子加热由右手边的最后一项给出，由公式(10)定义。电子能量通量由以下公式给出：

(15)

\mathbf{\Gamma}_{\epsilon} = -\mu_{\epsilon}n_
{\epsilon} \mathbf{E}-\nabla D_{\epsilon}n_{\epsilon}

平均电子能量是用 \bar{\epsilon}= n_{\epsilon}/n_e 计算的，\mu_{\epsilon} 是电子能量迁移率（m²/(V-s)），D_{\epsilon} 是电子能量扩散系数（m²/s），而项 S_{\epsilon} 代表由于弹性和非弹性碰撞造成的能量损失。这个项是平均电子能量的一个高度非线性函数，也是电子密度、背景数密度和等离子体化学的函数。这个源项的复杂性与本讨论无关，但《等离子体模块用户指南》给出了更多的细节。对于每个离子和中性物质，为每个物质的质量分数 w_k，求解一个类似的漂移-扩散方程：

(16)

\rho \frac{\partial w_k} {\partial t}
= \nabla \cdot \mathbf{j}_k + R_k

式中，下标 k 表示第 k 种物质。质量通量矢量 \mathbf{j}_k，表示由于双极场的迁移和浓度梯度的扩散而产生的质量迁移（kg/m² s），R_k 是反应源或汇（kg/m³ s）。同样，进一步的细节可以在《等离子体模块用户指南》中找到，与本讨论无关。

最后，求解泊松方程，以计算由电荷分离产生的双极电场：

(17)

\nabla \cdot \mathbf{E}= \frac{\rho_v}{\epsilon_0}

式中，\rho_v 是空间电荷密度（C/m³），\rho_v = e(n_i^+-n_e-n_i^-)，n_i^+ 是正离子总数，n_i^- 是负离子总数。

综上所述，微波等离子体 接口在一组合适的边界条件下求解了方程(10)，(12)，(14)，(16)和(17)。

TE 和 TM 模式传播

在二维或二维轴对称模型中，电磁波以横电波（TE）模式或横磁波（TM）模式传播。在 TE 模式下，横向上只有电场分量，传播方向有磁场分量。因此，COMSOL 只对高频电场的面外分量进行求解。在 TM 模式下，横向上只有磁场分量，传波方向上有电场分量，因此 COMSOL 只求解高频电场的面内分量。

TE 模式

在 TE 模式下，电子在微波时间尺度内不会经历任何高频电场的变化。这意味着，电子和电磁波之间的相位相干性只是通过与背景气体的碰撞而被破坏。电子和高频场之间相位相干性的缺失是导致电子能量增益的原因。因此，动量碰撞频率可以简单地由下列公式表示：

\nu_m = \nu_e

式中，\nu_e 是电子和中性物质之间的碰撞频率。

TM 模式

TM 模式导致电子在微波时间尺度上的面内运动，因此在高频电场显著的区域（电子密度等于临界密度的等值面），电子经历的时间平均电场可能是非零的。这破坏了电子和电场之间的相位一致性，导致电子获得能量。这是一个非局部动力学效应的例子，很难用流体模型来近似。然而，由于这种效应类似于与背景气体的碰撞，因此可以通过在动量碰撞频率上增加一个有效碰撞频率来近似非局部效应：

\nu_m = \nu_e + \nu_{\textrm{eff}}

式中，\nu_{\textrm{eff}} 是考虑到非局部效应的有效碰撞频率。这在参考文献1中有更详细的讨论，其中建议的有效碰撞频率不超过 \omega/20。

ECR 反应器

当对 ECR（电子回旋共振）反应器进行建模时，问题的复杂性又增加了一层。电子传递属性成为了静态磁通密度的张量和函数，而静态磁通密度可以用永磁体来创建。等离子体电导率也变成了一个完整的张量，并且是一个高度非线性的静态磁通密度的函数。此外，还需要考虑电磁场的所有三个分量。关于如何建立和求解 ECR 反应器模型的完整细节，可以在偶极微波等离子体源模型文件中找到。

在等离子体模块中使用微波等离子体接口

微波等离子体 接口可用于建立上述三种类型的波加热放电模型，但在建立这种模型时需要注意一些问题。在微波等离子体设置窗口中，“求解的电场分量”下有三个选项：

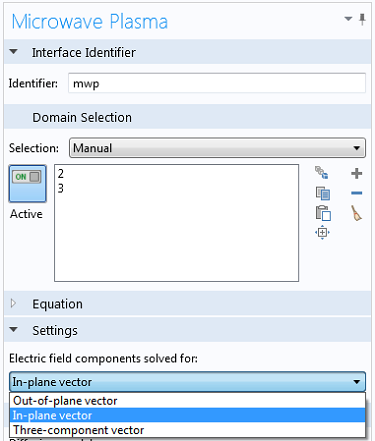
微波等离子体设置窗口。

选项如下：

面外矢量
- 该选项对应于 TE 模式
面内矢量
- 该选项对应于 TM 或 TEM 模式
三分量矢量
- 模拟 ECR 反应器时需要选择这个选项

共振区

只要等离子体频率低于建模域中任何位置的角频率，上述方程求解起来就相当简单。在 2.45GHz 的频率下，对应的电子密度为 7.6×10¹⁶ 1/m³，低于大多数工业应用。当等离子体密度等于这个值时，电磁波从传播波过渡到倏逝波。电子密度大于临界密度的微波等离子体的应用包括：

常压放电，其中电子密度可以比临界密度高几个数量级。
行波持续放电和表面波放电。要使表面波传播，电子密度必须高于临界密度。

可以通过激活等离子体属性部分的 “计算张量等离子体电导率”复选框对共振区进行平滑处理：

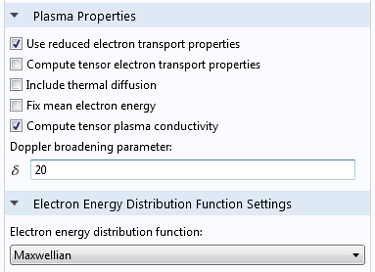
多普勒展宽参数 \delta，对应于用于以下计算有效碰撞频率的公式中的值：

\nu_m = \nu_e + \frac{\omega} {\delta}

因此，如上文所详述，参数值 20 是精度和数值稳定性之间的折衷选择。

沉积和反射的功率

当使用端口边界条件时，默认提供沉积功率和反射功率之和。在 COMSOL Multiphysics 4.4 版本中，也可以只指定沉积功率，如下面的设置窗口所示：

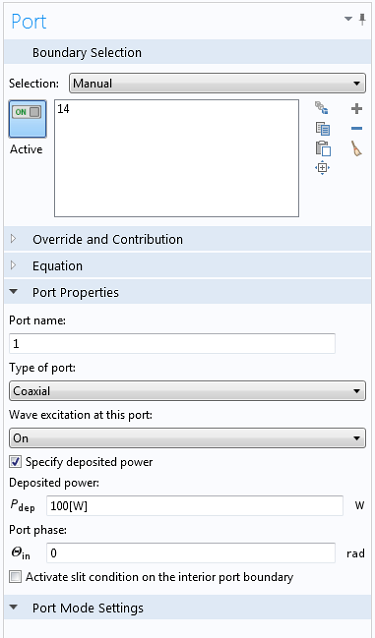
端口边界条件

使用这个选项可以得到一个更稳定的方程组，因为传递给电子的总功率保持不变。当使用“端口输入功率”选项时，根据等离子体的当前状态，一部分功率被沉积下来，一部分被反射到端口外。等离子体可以在很短的时间内从吸收非常小的功率变成非常大的功率，这可能会使问题在数值上不稳定或导致求解器采取极小的时间步长。

一些建模建议

以下是一些尝试帮助收敛和减少计算时间的提示和技巧：

通过使用端口边界条件中的“指定沉积功率”选项，或使用参考文献1中建议的方法（在偶极微波等离子体源模型中演示），固定放电的总功率。
从小于 1 的数值开始启动“多普勒展宽参数”，然后在模拟过程中将这个数值提高到 20。这将在开始时抹除共振区，然后逐渐使该区域越来越小。这可以通过定义一个截止值为 20 的斜坡函数来实现。

斜坡功能

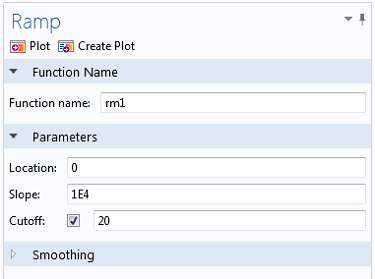
如果放电中的数密度非常高，它可能会以全表面波模式运行。在这种情况下，可能需要使用一个值为 10 的多普勒展宽参数。这将使模型在求解时更加稳定，但这个模型的准确性应慎重考虑。
在 TM 模式情况下，初始电子密度应低于临界等离子体密度。对于 TE 模式，这一建议并不是严格必要的。
负偏置电极可能会对放电产生重大影响，因为它可能会使临界等离子体密度的等值面偏离其无偏压的位置。最好的办法是用值为 5 左右的多普勒展宽参数来求解模型，然后慢慢增大其值。

以下建议适用于所有类型的等离子体，但值得再次提及：

必须通过网格充分求解德拜长度。如果你的几何体很大（即在 10 到 100cm 之间），并且电子密度很高（在 10¹⁸ 1/m³ 的数量级上），那么在靠近壁的地方就需要一个非常细的边界层网格。
在尝试更奇特的气体之前，先从简单的等离子体化学开始，如氩气。

求解器设置

求解器设置起着重要的作用，COMSOL 会根据模型的设置方式自动生成最佳的求解器设置。默认情况下，当使用 “端口输入功率”选项时，将执行下面提到的求解器设置。分离式求解器使用两个组：

所有的等离子体变量（电子密度、电子能量、离子密度、等离子体电势等）。
与电磁波有关的所有变量（高频电场、S 参数）。

当使用端口边界条件中的“指定沉积功率”选项时，求解器的建议被修改，使其分为三组：

所有的等离子体变量（电子密度、电子能量、离子密度、等离子体电势等）。
与电磁波有关的所有变量（高频电场、S 参数）。
一个名为沉积的因变量 P，它是一个用于固定沉积功率而不是总功率的微分代数方程。

示例

在 COMSOL 案例库中可以找到一个面内微波等离子体的示例。该模型使用的有效碰撞频率为 \omega/20，这使得功率沉积到电子上的区域更加平滑。从下图中可以看出，几乎所有的功率沉积仍然高度集中在临界电子密度的等值线上。

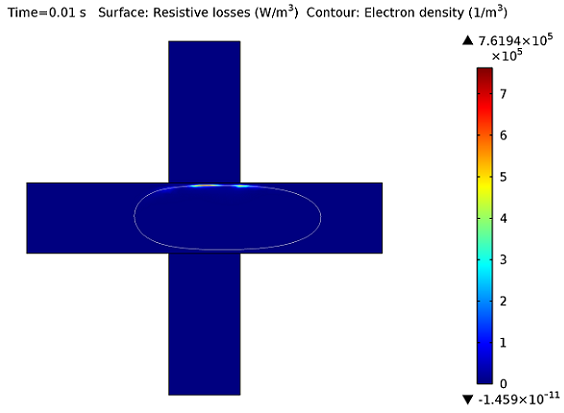
模拟微博等离子体：TM模式模型
高频场导致的等离子体中的功率沉积图。白色的等值线是临界电子密度的等值线。

进一步探索：对基于粒子的无碰撞加热的解释

在TM模式下发生的电子无碰撞加热可以用粒子追踪模块来演示。通过在临界等离子体密度的等值面上启动初始平均能量为 0.5eV 的粒子集合，可以计算出平均能量随时间的变化。下面的两幅图显示了在 TM 模式下无碰撞加热是如何发生的，而在 TE 模式下没有加热。

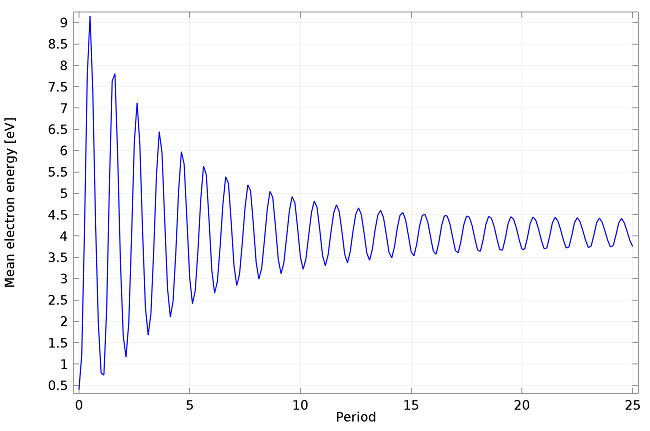
在 TM 模式下无碰撞等离子体中的电子平均电子能量绘图。
在临界等离子体密度的等值面上释放的 TM 模式碰撞等离子体中的电子平均电子能量绘图。即使没有碰撞，也会有净能量增益。

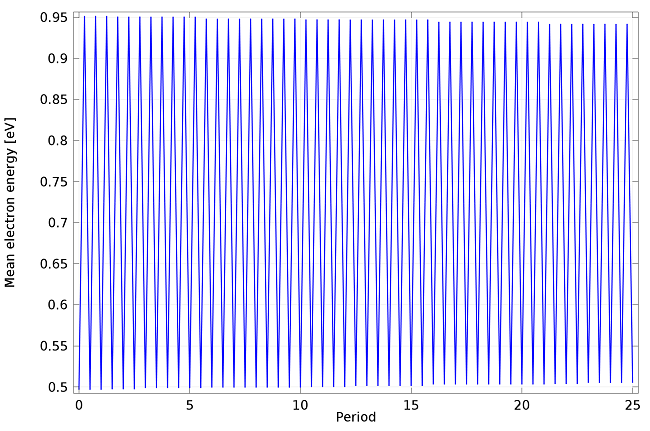
在 TE 模式下无碰撞等离子体释放的电子的平均能量绘图。
在临界等离子体密度的等值面上释放的 TE 模式碰撞等离子体中的电子的平均电子能量绘图。在若干个 RF 周期内，没有净能量增益。

参考文献

G.J.M. Hagelaar, K. Makasheva, L. Garrigues, and J.-P. Boeuf, “Modelling of a dipolar microwave plasma sustained by electron cyclotron resonance,” J. Phys. D: Appl. Phys., vol. 42, p. 194019 (12pp), 2009.
R.L. Kinder and M.J. Kushner, “Consequences of mode structure on plasma properties in electron cyclotron resonance sources,” J. Vac. Sci. Technol. A, vol. 17, Sep/Oct 1999.
Michael A. Lieberman and Allan J. Lichtenberg, “Principles of Plasma Discharges and Materials Processing”, Wiley (2005).

博客分类

浏览 COMSOL 博客

微波等离子体的原理和仿真方法