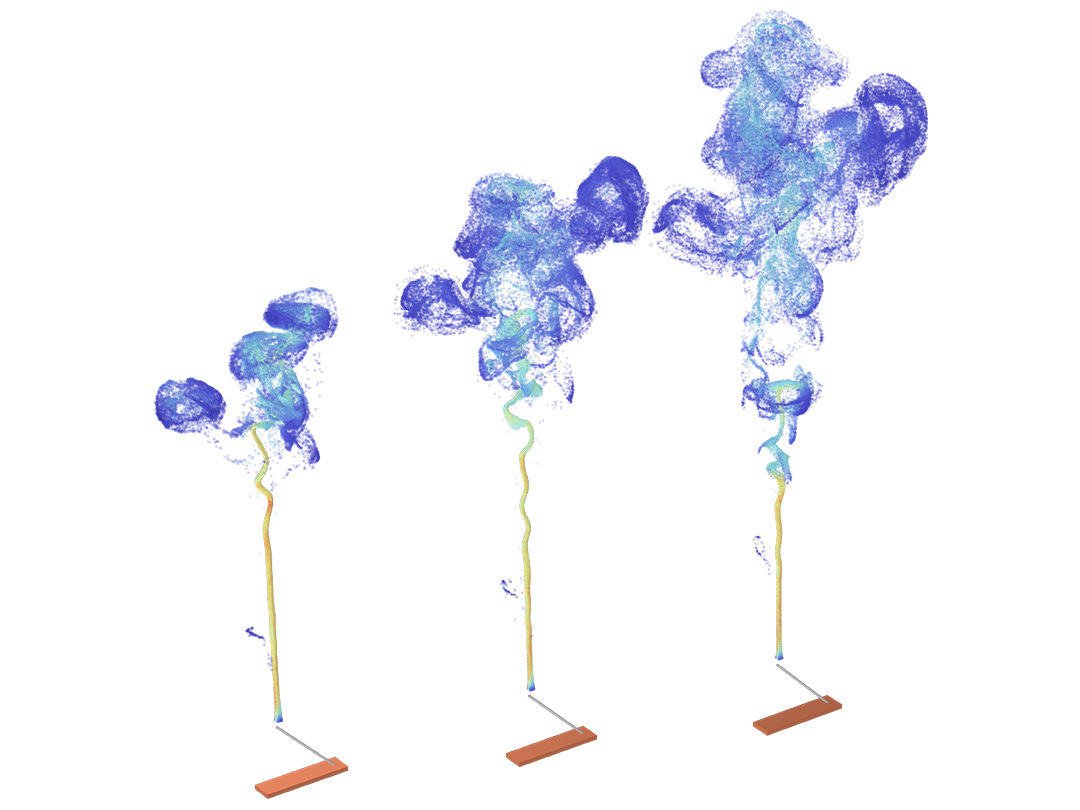带电粒子追踪
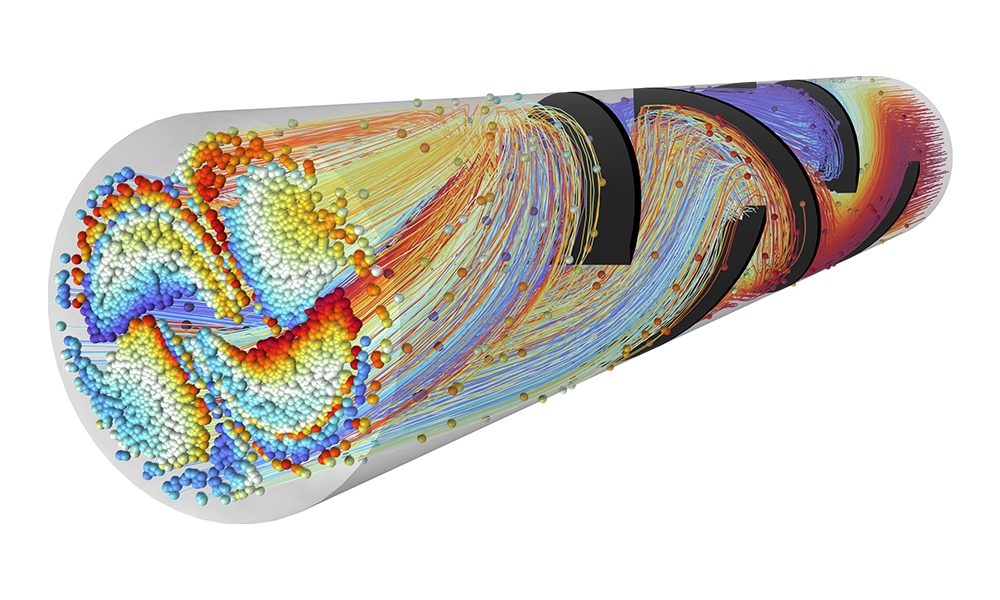
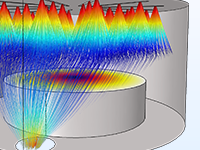
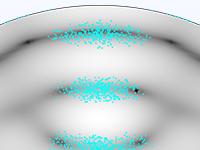
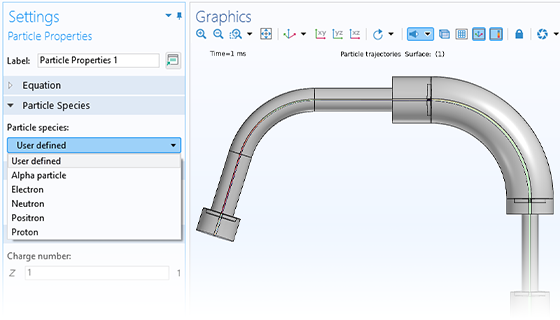
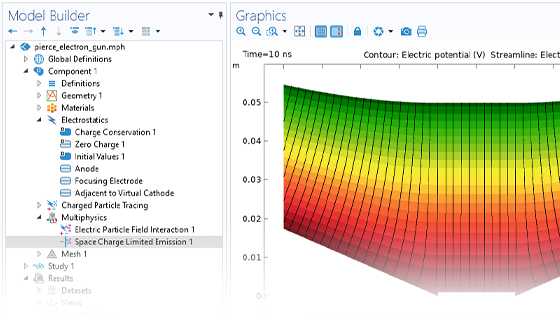
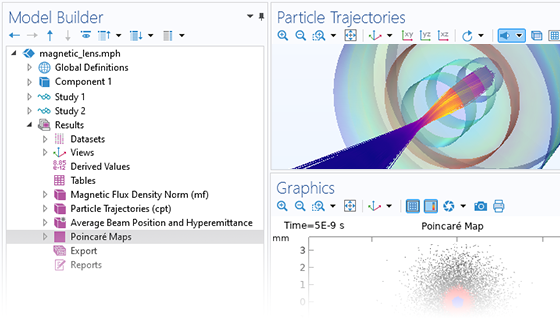
在光谱仪、电子枪和粒子加速器的设计中,准确预测离子或电子在场中的运动至关重要。对带电粒子产生影响的外加电磁场可以由用户自定义,也可以基于已有的仿真结果;外加电磁场可以是稳态或随时间变化的,可以是交变的,也可以来自若干场的叠加,如稳态和时谐交变场的叠加。
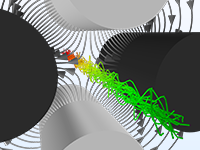
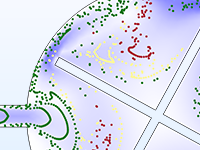
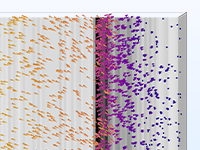
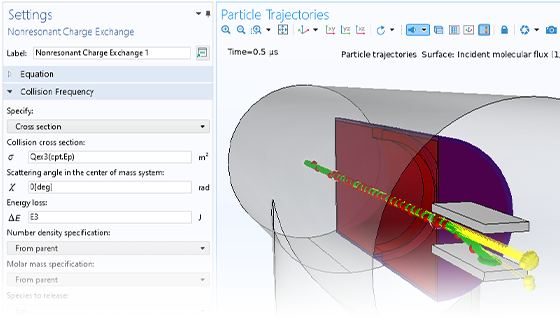
在实际情况中,粒子的运动很少发生在完美的真空环境中。粒子追踪模型可以转变为蒙特卡洛碰撞模型,以分析粒子与周围气体中的分子发生的随机碰撞,这种碰撞可能会导致粒子改变方向,甚至发生电离和电荷交换等反应。
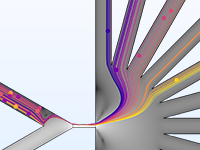
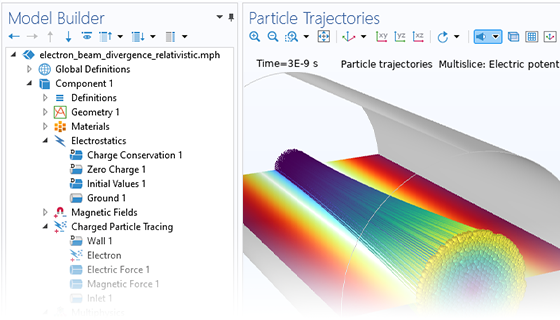
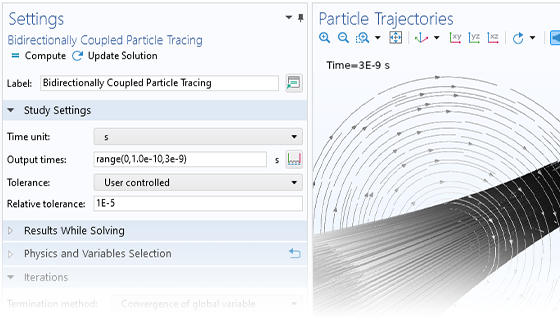
一般来说,简单的带电粒子追踪模型是单向耦合的,即先求解外加场,然后基于其结果计算粒子的受力来分析粒子的运动追迹。当带电粒子组成强度足够高的电流束时,则需要考虑粒子运动对场的扰动。针对这种情况,模块内置了相应的分析类型,使得操作更加简单便捷。