最新内容
如何使用 COMSOL® 模拟代谢反应网络
2021年 8月 4日
某些冰淇淋、布丁和糖果具有非常鲜艳的黄色,这种黄色来自维生素 B2。 该补充剂的制造是代谢反应网络的一个例子……

在 COMSOL Multiphysics® 中曲线拟合解数据
2021年 7月 27日
我们讨论了连续解数据的曲线拟合、正交性的概念,以及如何将解数据拟合到一组正交函数以进行简单方便的后处理操作。
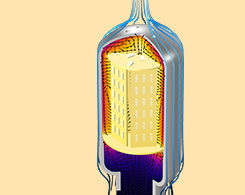
通过传热仿真分析 LED 灯泡设计
2021年 7月 22日
LED 灯泡被宣传为比传统灯泡更节能,但它们在将电转化为光方面的效率并非 100%,因此热管理成为重要的设计考虑因素。
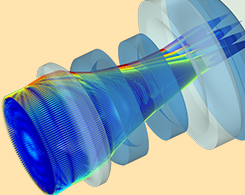
通过仿真优化微型相机模组设计
2021年 7月 20日
灯光、相机、模拟:了解有助于定义紧凑型相机模块 (CCM) 性能的因素,以及如何使用光线追踪来分析其设计。
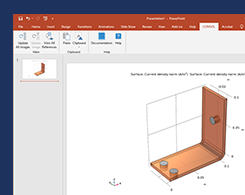
如何将 COMSOL 图像链接到 Microsoft® PowerPoint® 演示文稿中
2021年 7月 16日
您知道您可以在 Microsoft®PowerPoint® 演示文稿中轻松地从 COMSOL Multiphysics® 导入、更新和替换模型图像吗?

在 COMSOL Multiphysics® 中模拟点蚀
2021年 7月 13日
当全面腐蚀过程持续进行时,金属表面可能会出现凹坑,这也被称为 Evans drop 实验。
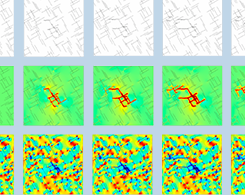
裂隙介质全耦合流体力学建模
2021年 7月 1日
了解裂隙地质介质中固体变形与流体流动之间的耦合关系,对于解决地球科学和岩土工程中的许多核心问题,例如地下挖掘、油气开采、碳封存、地热生产和废物处理,具有重要的意义。

设计用于红外应用的抗反射微结构
2021年 6月 29日
探索 2 种微结构设计如何在特定波长光谱内将硅 (~70%) 和碲化镉锌 (~79%) 的体透射率提高到 90% 以上。



