第 1 部分：模拟线性系统的谐波激励

在许多工程案例中，我们可以假设目标系统上的激励和响应是随时间变化的正弦波。当这个假设成立时，就可以使用频域分析方法，这种方法会带来一些非常高效的求解技术。本文我们将复习一些基本概念，以及可以做出此假设的条件，同时讨论采用的各种求解方法。

工程和科学中的时谐载荷

在固体力学、声学、电磁学等工程学科中，我们经常可以假设存在正弦波的激励。例如，汽车上一个不平衡的车轮会导致正弦时变化的力，使车辆的结构以与车轮旋转相同的频率振动。在声学中，当扬声器膜在一个或几个频率下被驱动，会导致相同频率的声波辐射。同样，在电磁学中，输电线在一个恒定的频率下运行；手机天线在一个离散的频率范围内传播电磁波；激光输出几乎是单色、单频率的光。尽管涉及完全不同的学科，但在这些案例中，需要了解的建模方法却惊人地相似。

左图：不平衡的轮胎只是可能发生时谐波载荷的一个例子。图片由CC BY 2.0授权，通过Flickr Creative Commons许可。右图：汽车轮辋的配重块。

控制这些不同案例的偏微分方程都具有相同的一般形式：

(1)

其中，u=u(\mathbf{x},t) 是我们感兴趣的随空间和时间变化的场（即结构问题的位移或声学问题的压力）。M，K 和 C 项代表不同的材料属性，分别被称为质量项、刚度项和阻尼项。术语 F=F(\mathbf{x},t) 表示域上的分布式载荷。也始终存在一组边界条件，用于表示系统上的载荷 f=f(\mathbf{x},t) 和约束 g=g(\mathbf{x},t)。边界载荷通过 Robin 边界条件 施加，该条件包含表示边界吸收或边界阻抗可以为零的项。载荷 f 和约束 g 可以是零(齐次)或非零(非齐次)边界条件。

我们来看一个上述等式的一个最简单的例子：一个简单的谐波振荡器，如下图所示。

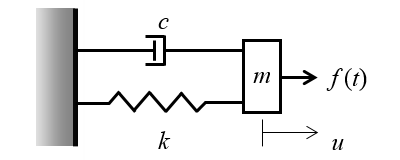
一个简单的谐波振荡器，其中弹簧和阻尼器将质量连接到刚性壁。施加的时变力使质量块来回振荡。

现在，假设我们也有一组初始条件 u(\mathbf{x},t=0)=u_0，就可以计算出这个系统随时间变化的位移响应。下图显示了质量块在施加载荷 f(t)=\sin(\omega t) 和初始条件 u_0=0 下的位移。在这些条件下，质量块从零开始来回振荡。经过一段时间的初始启动时间后，位移变为周期性;它以恒定的角频率 \omega 重复正弦波，并且与初始条件无关。

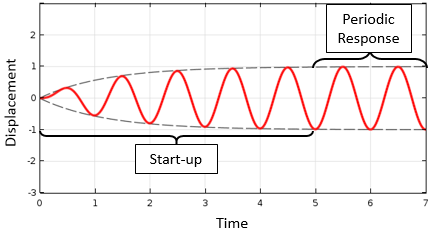
简单谐波振荡器对正弦激励的响应。初始条件为零开始，随着时间推进，位移最终表现出周期性。

这里的数据可能比我们真正需要的要多得多。例如，我们可能只对总启动时间感兴趣，而不是启动期间的时间演变。此外，在启动期之后，我们可能只关心位移的大小。因此，在时域中求解这样的问题并不是真正必要的;相反，我们可以将它变成所谓的频域 问题。

但是，频域分析依赖两个重要的假设。首先，系统上的所有时变载荷和约束必须在相同的固定频率下正弦变化。其次，所有载荷、约束和材料属性必须独立于解。在这两个假设下，我们可以推断出解的形式如下：

它可以对时间进行微分，并放入原始的控制偏微分方程中，从而得到：

(2)

它提供了控制方程的频域形式。请注意，场将是复值，因此包含了有关解量级和相位的信息。这个偏微分方程和边界条件是线性的，因此求解起来非常简单，就像我们之前关于求解线性静态有限元模型的博客中所描述的那样。现在，让我们更深入地研究这类问题的各种求解技术。

分析频域中的问题

COMSOL Multiphysics^® 软件包含一套不同的算法，适用于求解上述方程（等式(2))。最直接的方法是频域 求解器。该求解器将单个频率或离散频率范围作为输入进行仿真。

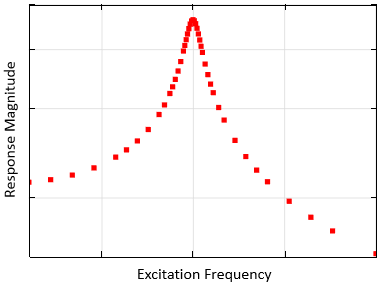
例如，我们可以在一系列激励频率下求解前面的简单谐波振荡器问题，得到类似于下图的图，该图说明了不同激励频率下的位移大小。无论涉及哪种物理场，频率响应始终与下面的曲线类似。响应与频率曲线中将有一个最大值，对应于系统的谐振频率。这个最大值两侧的响应下降，并且可以使用半峰全宽的带宽来计算品质因子 Q。品质因子特别有用，因为它可能与前面描述的系统启动时间有关。

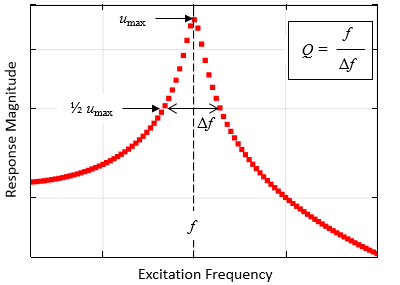
绘图表示在一组离散频率下求解的谐波振荡器在频域中对正弦载荷的响应。可以从这样的图中估计出谐振频率和品质因子。

使用频域求解器求解这类问题时，COMSOL Multiphysics 软件会按顺序求解每个指定的激励频率。因此，求解时间将与求解的频率数量成比例地增加。有两种方法可以缩短求解时间：网络浮动许可证提供的集群扫描 选项或渐近波形估计 (AWE)求解器。

使用群集扫描选项时，软件会自动将频率列表细分为单独的范围。然后，这些范围中的每一个频率都在一个集群的不同计算节点上被求解。这样做的好处是，可以根据需要使用任意数量的集群节点极大地并行化计算。甚至可以将模型设置为每个频率范围使用不同的网格 ，如果你的频段激励范围非常宽，这是一个有利的因素。软件将自动在单个模型中重新组合在集群的各个节点上计算的解。下图显示了如何将频率扫描分解为几个区间并在集群的不同节点上求解。你可以在有关集群计算的 COMSOL 博客上了解更多信息。

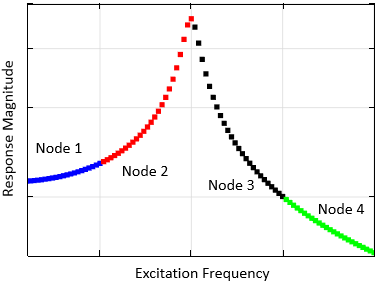
与之前相同的频率扫描，但在集群的不同节点上求解的频率范围不同。

使用 AWE 求解器时，软件将搜索感兴趣的频率范围，并在区间内连续添加离散频率的计算点，以获得响应与频率曲线的良好分辨率。这个方法的计算过程如下图所示。请注意观察AWE求解器如何在共振点求解了更多的频率点，以及在响应随频率逐渐变化的区域求解更少的频率点。这种方法可以与集群扫描选项结合使用。

AWE 求解器在响应随频率显著变化的范围内引入了额外的计算点。

到目前为止讨论的所有求解方法都给出了相似的响应曲线，尽管求解时间要求不同。这些解决方案有助于了解系统在不同激励频率下的响应方式。就像前面所表述的，我们还可以使用这样的曲线来估计系统的谐振频率和品质因子。事实上，有时我们仅对这两个量感兴趣。这带来了另一种称为特征频率 求解器的求解方法。

在求解特征频率问题时，软件实际上求解的模型与前面所示的控制偏微分方程所描述的模型略有不同。由于我们对共振的固有频率感兴趣，因此所有非均匀载荷和约束都更改为它们的均匀(零幅度)形式：

(3)

当求解这种形式的控制方程时，将计算系统的所谓特征值，\lambda = -j \omega + \delta。通过复值特征值，我们可以获得共振频率 f=\omega/2\pi 和品质因子 Q=f/2\delta。复值特征值是由于系统中的损失而产生的，即非零阻尼项C，或复值质量 M，刚度 K 或吸收项 A。如果没有损耗，则品质因子是无限的，软件仅返回谐振频率。软件还返回场变量的解 \tilde u，用于可视化系统在共振时的行为。这个解通常称为振型或特征模态。

让我们来看一个非常简单的结构问题的特征频率分析的样本结果：一个两端固定的细长梁结构。面内弯曲模式的共振频率和振型如下图所示。

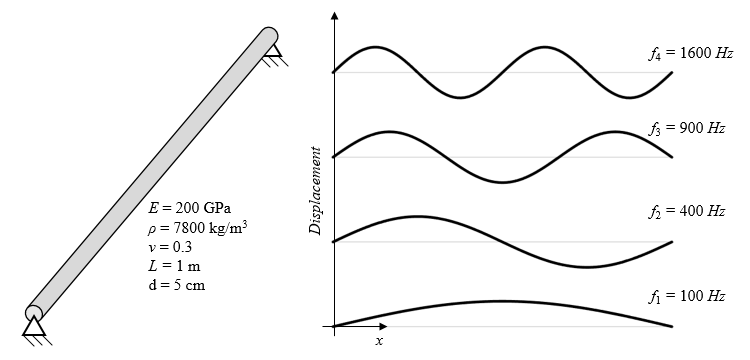
一端固定的圆形梁光束的前四个谐振频率和振型。

这些特征值结果实际上可以用于另一种称为频域模态 研究的研究类型，即所谓的两步研究。在第一个研究步骤中，计算用户指定的特征频率和振型数量。在第二步中，使用这些特征值解的线性组合来重建频率响应行为。随着使用更多的特征值，这种方法变得更加准确。可以在下图中看到这一点，该图对比了频域求解器的扫频结果和频域模态求解器使用不同数量的特征值参与计算的结果。

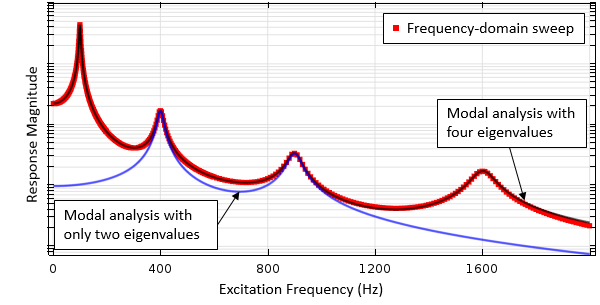
频域扫描法和频域模态法使用不同数量特征值时的结果比较

结束语

对线性系统的谐波激励进行建模是许多解析问题中的重要步骤。今天，我们介绍了 COMSOL Multiphysics 为求解这类模型提供的各种求解算法。我们需要牢记所有这些建模技术，因为不同的模型将受益于不同的算法。

那么，对于非线性系统呢？这些系统对谐波激励的响应非常不同，包括产生低次或高次谐波。我们在即将发布的博客中将对此进行重点介绍。COMSOL 提供了许多强大的并且可以轻松使用的工具，用于解决这些复杂情况。敬请期待！

线性系统谐波激励建模的各种应用

• 想自己尝试在 COMSOL Multiphysics 中对线性系统的谐波激励进行建模吗？浏览下面的案例模型列表，找到最适合你的工程分析重点的案例：
  • 弯头支架的各项分析，结构力学教程，具有频域、特征频率和频域模态分析
  • 使用各种频域求解器分析亥姆霍兹共振器，声学教程，包括频域、特征频率和频域模态分析
  • 射频线圈，具有频域和特征频率分析的波电磁学教程
  • 消失模圆柱腔滤波器，一个波动电磁学示例，包括频域和 AWE 分析
  • 级联矩形腔滤波器，波动电磁学教程，具有频域和频域模态 AWE 分析
• 阅读相关博客文章：提升带通滤波器类器件建模的方法
• 对这个主题还有其他疑问吗？请随时与我们联系