使用铣削约束进行拓扑优化

拓扑优化由于具有极高的设计自由度，因此能实现极致的设计性能，但通过拓扑优化产生的设计往往无法通过传统的制造技术去实现生产。一直以来，研究用于拓扑优化的制造约束都是一个热点课题。COMSOL Multiphysics^® 软件支持模拟铣削约束，在这篇文章中，我们将解释如何使用这种功能并介绍一些示例。

拓扑优化

密度法是进行拓扑优化的最常见方法，在 COMSOL Multiphysics 中可以通过密度模型 特征实现。最常见的应用是在结构力学领域，通常需要正则化才能获得有意义的结果。密度模型 特征支持使用基于偏微分方程（PDE）的滤波器，也就是使用亥姆霍兹滤波器 进行正则化。下图显示的结构力学示例显示了参数优化、形状优化和拓扑优化之间的差异。有关更多详细信息，请参阅关于拓扑优化的博客文章“通过密度方法进行拓扑优化”。

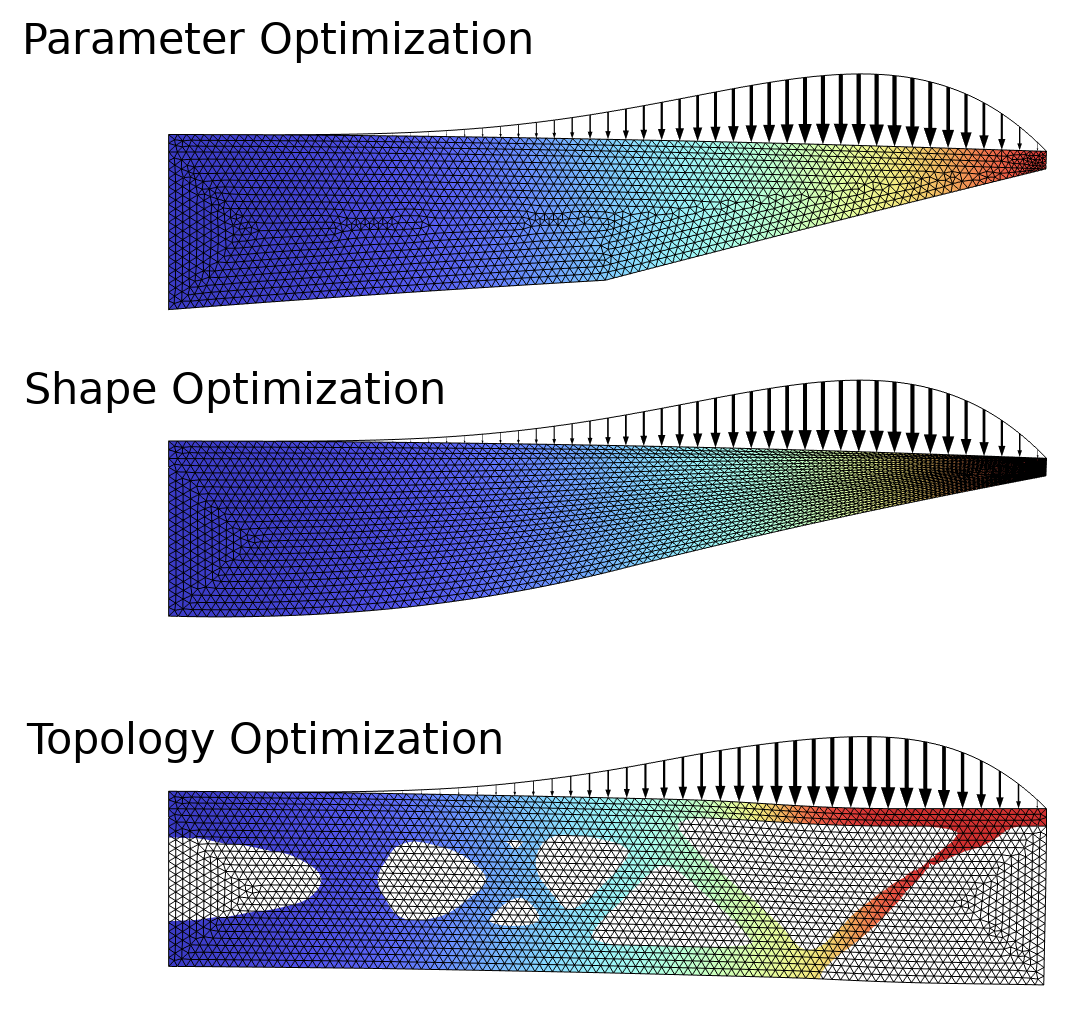
图1 梁的设计优化模型示例，分别使用了参数优化、形状优化和拓扑优化解决结构力学中的问题。目标是在约束右上角位移下使梁质量最小。只有拓扑优化才能在设计中引入孔。

铣削约束

在密度模型 特征中，铣削约束是参考学术文献出版物（参考文献 1）来实现的。它的基本概念是使用一组在铣削方向 \hat{m}_\mathrm{mil}^i 上具有对流的对流方程：

第一个方程是亥姆霍兹滤波器，使用控制变量场 $\theta_c$ 来计算最小长度尺度为 $L_\mathrm{min}$ 的过滤场 $\theta_f$。对流方程（第二行）位于亥姆霍兹滤波器和投影之间。源项 R_\mathrm{mil} 的长度尺度通常可以根据网格大小设置。数值参数 $p_\mathrm{mil}$ 与铣削变量 \theta_m^i 的聚合（指数）相关。对于 2~3 个铣削方向，数值 10 是合适的，但对于大量铣削方向可能需要高的值。投影斜率 \beta 也是如此，它比平时起着更重要的作用，因为投影的输入（第三行）通常明显大于 1。投影点 \theta_\beta 固定为 0.5。使用投影场 \theta 对密度进行插值，对固体各向同性材料使用罚函数（SIMP）对刚度进行插值（最后一行，\theta_p）。通常，使用 p_\mathrm{SIMP}=3 避免最终设计中的灰度，当数值问题导致投影场略为负值时，使用 \theta_\mathrm{min}=10^{-3} 来确保鲁棒性。

我们只考虑单一材料的优化，因此体积 V 等同于质量 M，可以通过积分投影场并与密度 \rho 相乘来计算：

在公式中引入铣削约束会引入更多的局部最小值，并且在一系列优化被求解的情况下使用连续性可能是有益的。这大多数情况下是一个三维问题，所以与我们文中展示的第一个示例无关。

示例 1：二维梁结构

下图是对示例 1 的问题描述，与上一节中的问题一样，它也是一个结构力学问题，目标是约束右上角位移时使质量最小。但是这一次，由于施加了铣削约束，材料无法自由分布。此示例有两个与坐标轴重合的铣削方向，这意味着材料只能通过来自左侧或下方的“去除工具”去除。

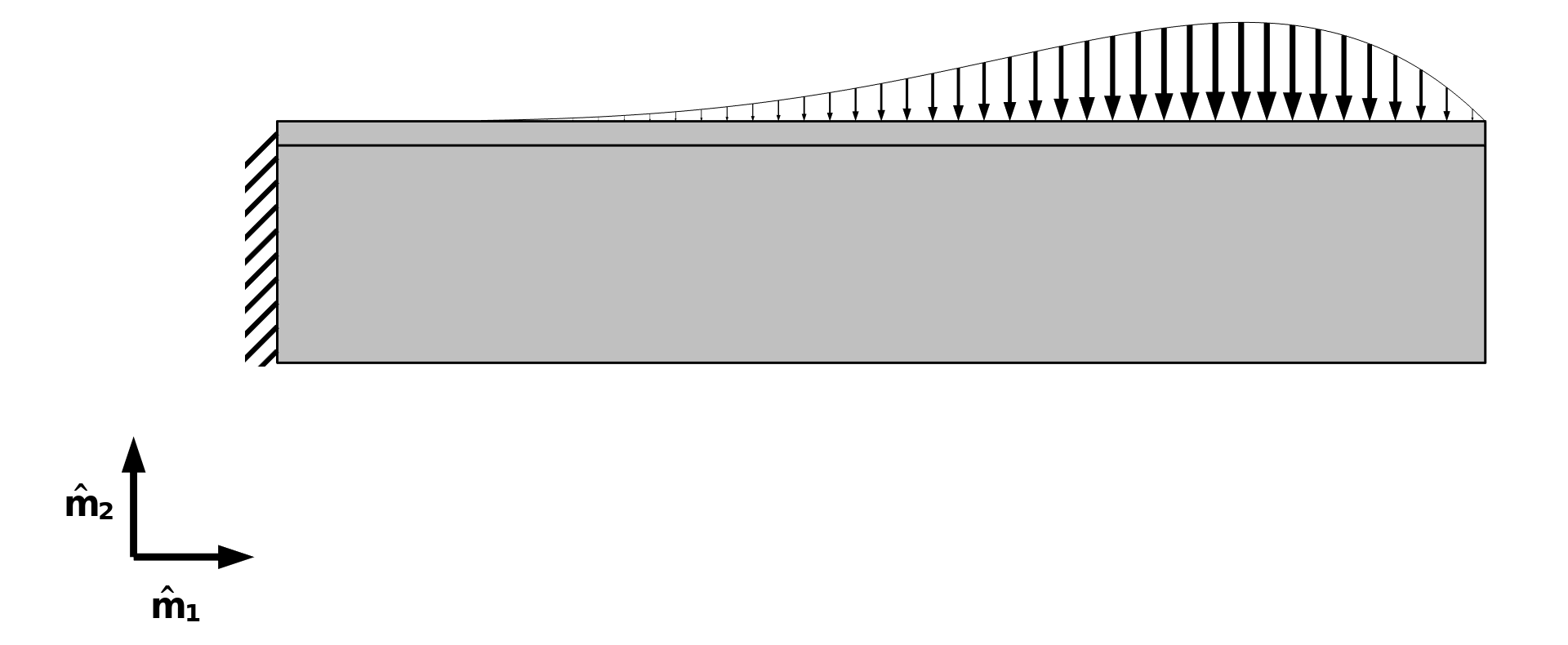
图2.带铣削约束的梁拓扑优化模型的问题表述，包括铣削方向 \hat{m}_1 和 \hat{m}_2，梁的左端是固定的，顶部边界则承受分布载荷。

如下图所示，密度模型 特征具有铣削约束的设置。启用投影非常重要，而且很多时候还需要将控制变量场初始化为明显小于 1 的值。

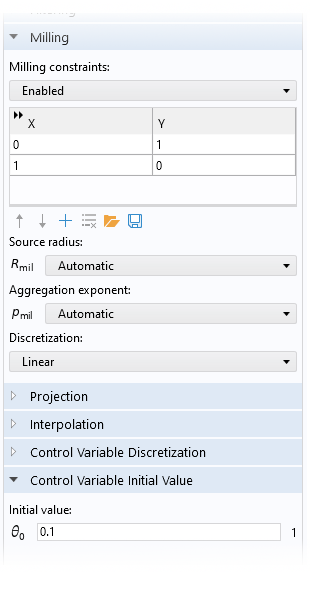
图3. 启用铣削约束的示例，显示了 密度模型特征的用户界面（UI）。 投影部分在图中处于折叠状态，但在本例中，投影是使用默认斜率和投影点启用的。

在优化 研究步骤中，定义了优化问题。MMA 是推荐的优化求解器方法，有时不使用全局收敛和/或移动限制是有益的。虽然使用默认的全耦合求解器也可以很好地实现优化求解，但上一节中的方程组包含一个用于过滤的线性方程，并使用两个用于对流的线性方程组形成单向耦合。最后一个方程与固体力学 接口相关的方程组，还有另一种单向耦合。因此，使用分离式 求解器求解要快得多。在这个示例中，分离式 求解器将计算速度提高了约 2 倍。

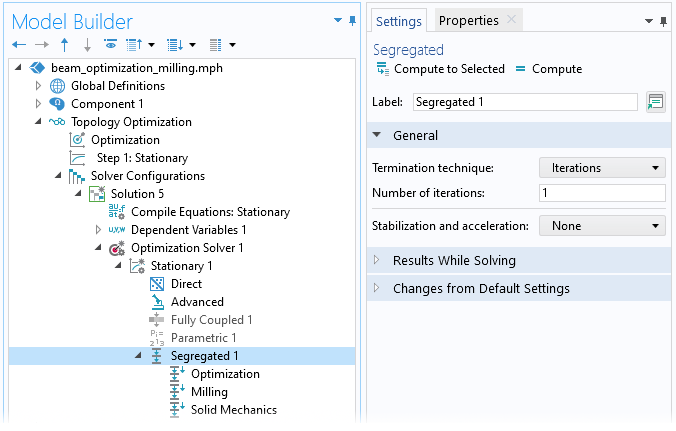
图4.线性单向耦合问题的分离式求解器设置。使用 固体力学接口定义线性系统时，甚至可以将求解器限制为单次迭代，来节省一点计算时间。或者，可以在 固体力学接口步骤中使用多次迭代。

优化结果如下面的动画所示。在二维建模中，引入铣削约束可以防止产生孔，因此从这个意义上说，拓扑实际上是合适的，并且本质上该方法被简化为一种允许大变形的形状优化。因此，最适合使用铣削约束的是三维建模，我们将在接下来的两个示例中进行介绍。

图示为不同的迭代次数绘制的材料体积因子 \theta。无铣削约束的拓扑优化结果见图 1。

示例 2：三维扭转球

铣削约束降低了设计自由度，这应该更容易找到一个好的最优方案，但是由于还引入了非线性，在实践中，很容易得到局部最小值。如果分别在投影斜率 SIMP 指数 \beta 和 p_\mathrm{SIMP} 中使用连续策略，就可以在某种程度上避免这种情况。这种策略通常会产生良好的 3D 设计，但参数的选择可能对问题和铣削约束的数量很敏感。

考虑一个扭转球示例，这是一个经典的具有扭转荷载工况的基准问题，如下图所示。目标是最大限度地提高固定箱体和承受扭矩的箱体之间的刚度。这两个箱体沿扭矩轴分离，设计受到质量约束（相当于体积约束）。

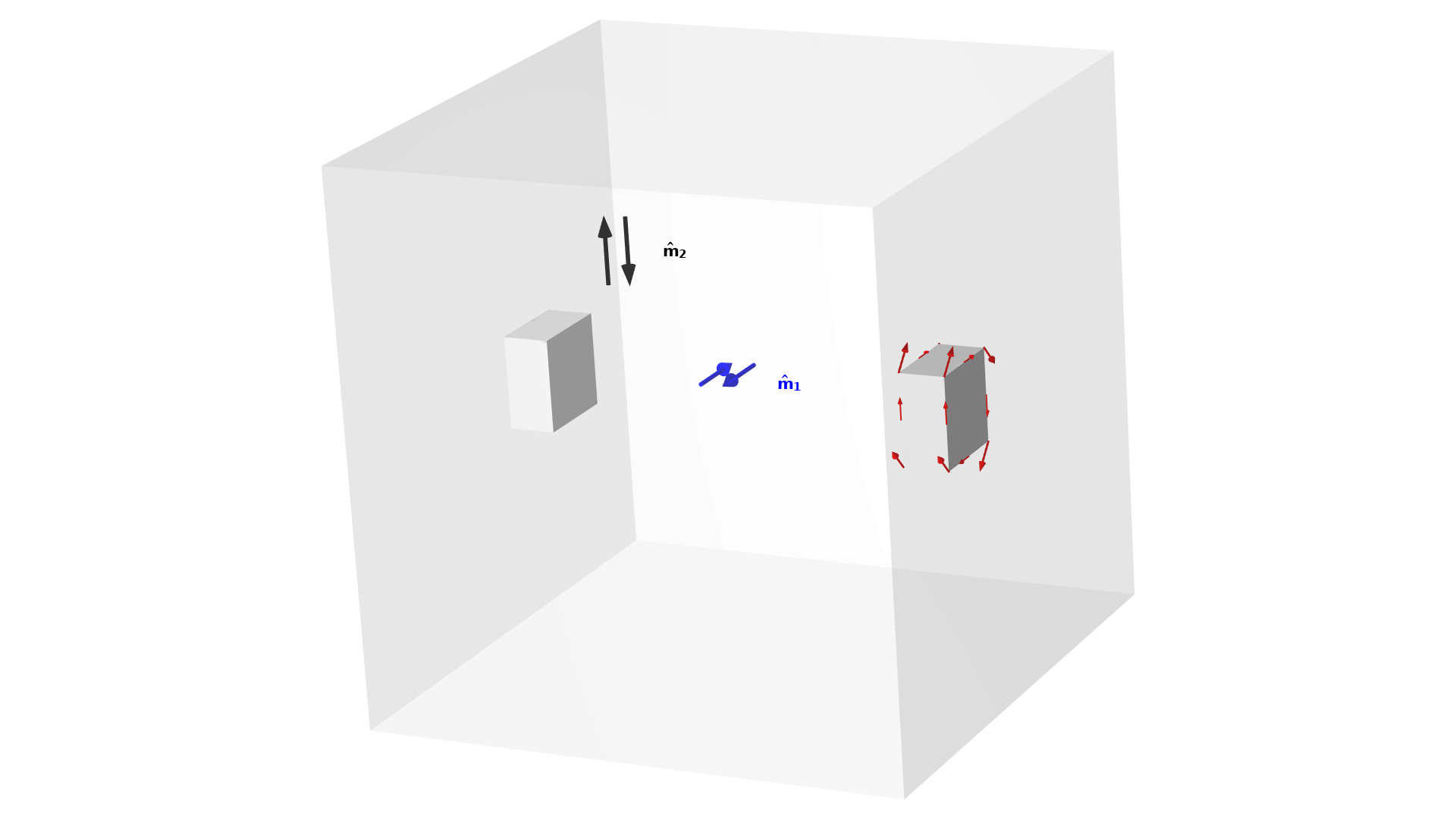
图5. 扭转球问题的设置。有 4 个铣削方向，但强加了对称性，因此只需要考虑 2 个铣削方向。

下面的动画显示，在带和不带铣削约束的情况下的优化结果。密度模型特征支持对流方程的线性离散化和常数离散化，这个示例演示了输出不太平滑的常数选项。

用灰度图绘制了带（右）和不带（左）铣削约束优化时 0.5<\theta 的单元。每次迭代都会显示目标值和连续参数。

对不带铣削约束的优化结果是一个含内腔的封闭球形设计。这种设计不可能用传统的减材制造方法制造，但非常适合测试制造约束。对带铣削约束进行优化会产生一个不含内腔的设计，但这是以柔度（刚度的倒数）高出约 40% 为代价的。如果不添加更多铣削方向，很难显著改进优化目标，但是拓扑对连续的细节还是很敏感的。

示例 3：轮辋

最后一个例子是一个三维结构问题。目标仍然是使受体积约束的刚度最大，但这个示例与前面的问题有三方面不同：

• 使用 12 个载荷工况而不是 1 个
• 扇区对称仅适用于设计（而不是物理场）
• 对流方程使用了线性离散化

使用 12 个载荷工况会导致更多的计算工作。但是，这些载荷工况可以并行计算，因此，如果有合适的硬件，计算时间不一定会大幅增加。

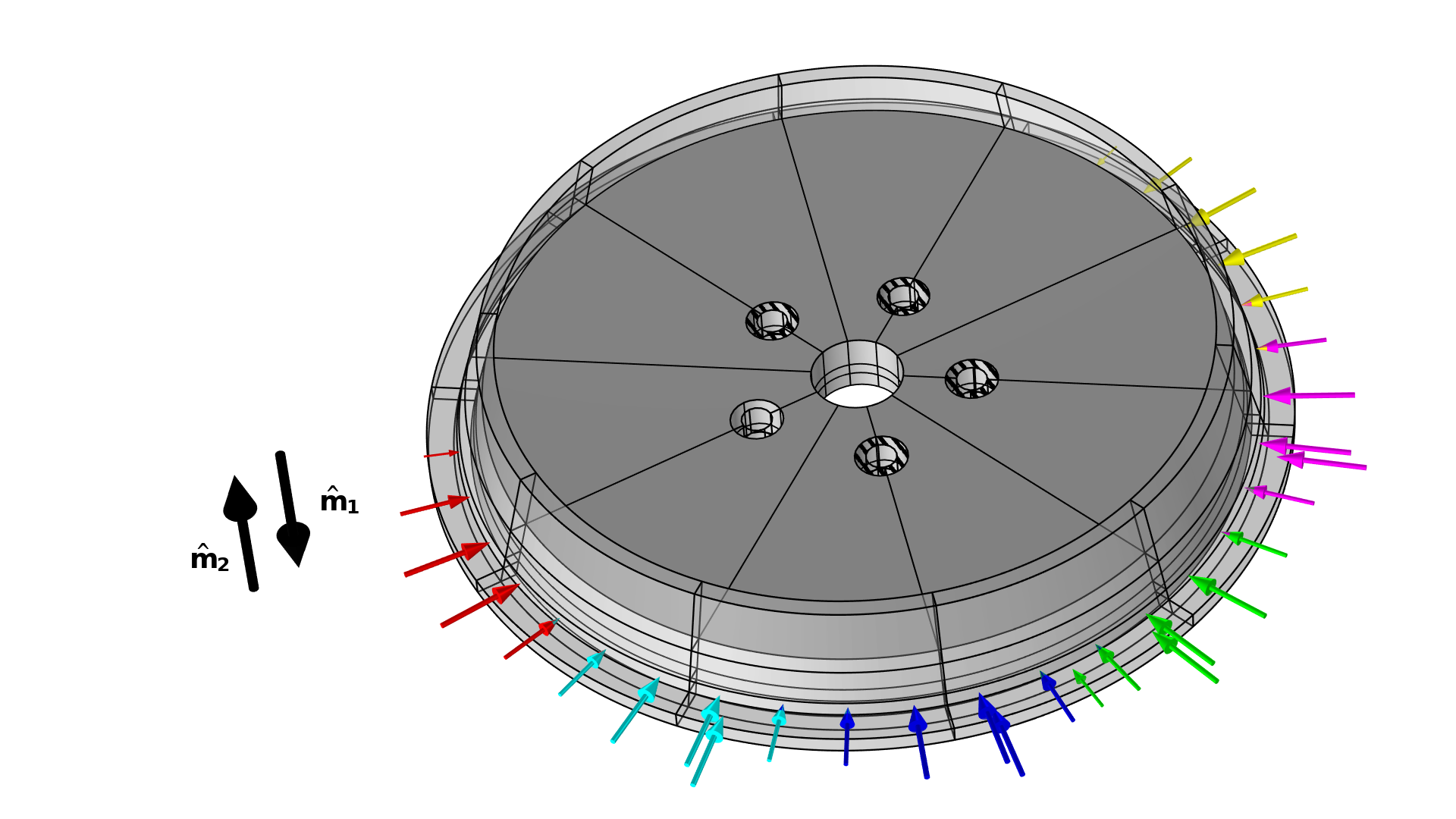
图6. 用各种颜色显示的载荷工况和用黑色显示的铣削方向来说明轮辋问题的设置。请注意，在轴向方向上还有第二组设置，并且只有四个螺栓孔受约束。

扇形区对称性是使用广义拉伸 算子强加的，该算子将设计变量从“控制扇形区”映射到其他扇形区。

每次迭代都会显示目标值和连续参数。用灰度图绘制了带（右）和不带（左）铣削约束轮辋优化时）0.5<\theta 的单元。

在这个示例中，使用铣削约束进行优化生成的是含非分支辐条的简单拓扑。辐条的横截面具有 z 形形状，以增加两个方向的弯曲刚度。

对合适的体网格进行验证

与密度方法相关的隐式几何表示总是会引入一些误差。这是由于非零刚度，以及实体和空隙之间过渡区域中的单元与较差的刚度质量比有关。后者的影响通常占主导地位，因此隐式几何表示法常常低估了性能。为了验证设计的性能，可以使用过滤器数据集将设计转移到一个新组件上。我们可以使用布尔表达式剪切单元，这样大部分网格就可以被回收，也可以将设计作为一个新的几何体导入并从头开始创建新网格，如下图所示。物理场接口（和特征）支持复制粘贴功能，因此简化了新组件的设置。物理场接口的选择将被重置，但在几何和定义下定义的所有选择都将自动转移到新的组件中使用。

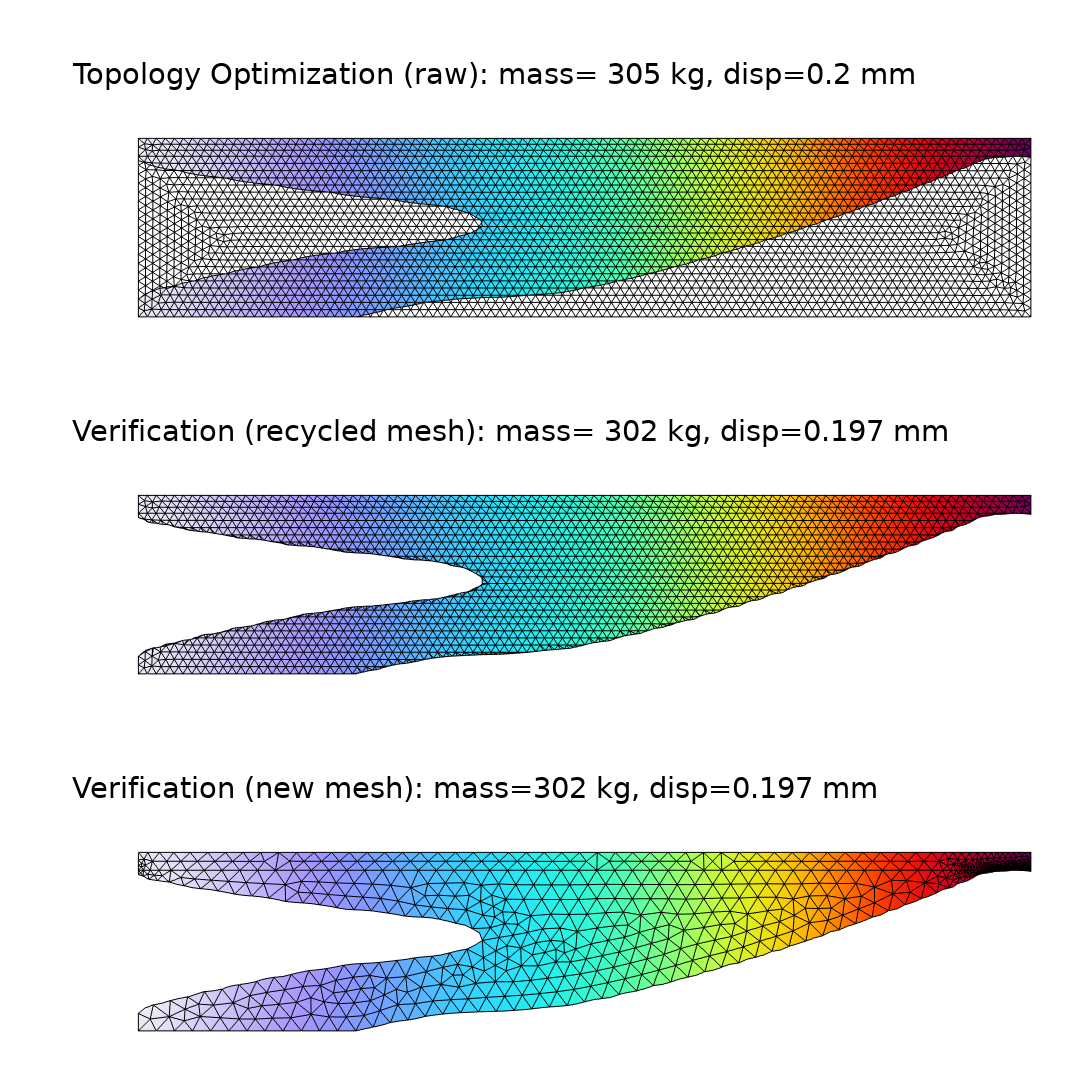
图7.绘制了第一个示例（上图）的原始拓扑优化的位移场和网格。显示了带（中心）和不带（底部）回收网格的方法。在所有情况下，都绘制了示例的质量和约束。

下一步

如果您想要了解与进行拓扑优化有关的特征和功能的更多信息，请查看优化模块的介绍，单击下面的按钮，了解更多内容。

参考文献

1. L.C. Høghøj and E.A. Träff, “An advection-diffusion based filter for machinable designs in topology optimization,” Computer Methods in Applied Mechanics and Engineering, vol. 391, p. 114488, 2022; https://www.sciencedirect.com/science/article/pii/S0045782521007003