递归和递归定义的几何对象

递归定义的几何结构在工程应用中可能很有用，比如宽带天线和超材料。关于一些应用的简要概述，请查看之前一篇关于分形的博客。本篇博客，我们将看看如何通过算法快速生成这种几何对象。

使用方法和 App 开发器创建递归定义的几何对象

我们可以使用 App 开发器中的方法编辑器创建可以执行几乎任何类型的建模任务的方法，包括几何建模。我们很容易忽略这样一个事实，那就是方法可以通过在递归循环中调用自身的方法来支持递归。

本文，我们将通过两个著名的递归结构的例子来演示递归：二维的 Sierpinski 地毯和三维的Menger 海绵。这些例子的代码很短，因此我们可以完整地将它们列出，并且在文末有下载这些示例子的链接。

Sierpinski 地毯

下图中显示的方法，create_carpet，根据一个输入参数层 将递归运行到某个递归层。它将限制设置为 5 个层，以避免创建过大的几何图形。(如果你认为你的计算机可以处理大的几何图形，你可以更改这个限制。)

if (level < 1)
error("Carpet level needs to be at least 1.");
if (level > 5)
error("Carpet level needs to be at most 5.");

counter = 0;
model.component("comp1").geom("geom1").feature().clear();
model.component("comp1").geom("geom1").autoRebuild("off");
double cx0 = 0, cy0 = 0;
double si0 = 1;
carpet(level, cx0, cy0, si0);
model.component("comp1").geom("geom1").runPre("fin");

输入在方法的设置 窗口中定义的参数层，如下所示。

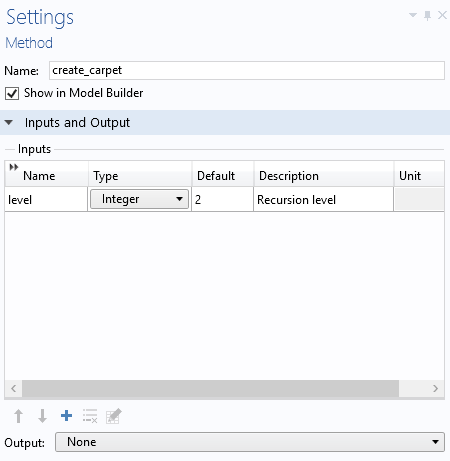
反过来，方法 create_carpet 调用下面列出的主要递归函数——地毯，使用了四个输入参数：递归层、中心 x 坐标和 y 坐标，以及当前的边长。

输入参数在方法的设置 窗口中被定义，如下所示。

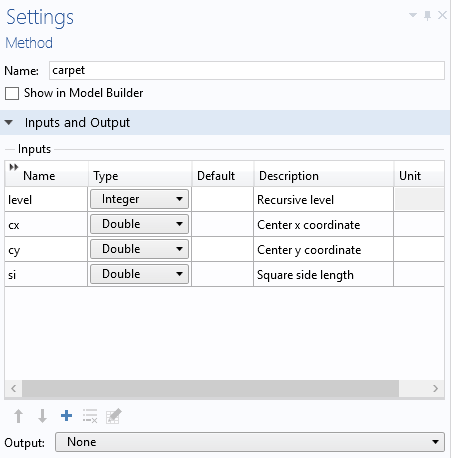
下图所示是方法地毯 的代码：

int l = level;
double posx, posy, si1;
String strix;
int l1;
for (int i = 0; i < 3; i++) {
  for (int j = 0; j < 3; j++) {
    posx = cx+i*si-si;
    posy = cy+j*si-si;
    strix = toString(i)+toString(j);
    if ((Math.abs((i-1))+Math.abs((j-1))) > 0) {
      if (l == 1) {
        counter = counter+1;
        model.component("comp1").geom("geom1").create("sq"+strix+"C"+toString(counter), "Square");
        with(model.component("comp1").geom("geom1").feature("sq"+strix+"C"+toString(counter)));
          set("base", "center");
          set("size", new double[]{si});
          set("pos", new double[]{posx, posy});
        endwith();
        model.component("comp1").geom("geom1").feature("sq"+strix+"C"+toString(counter)).label("Square"+strix+"C"+toString(counter));
      } else {
      l1 = l-1;
      si1 = si/3;
      carpet(l1, posx, posy, si1);
      }
    }
  }
}

为了获得方形对象的连续编号，使用整数变量计数器（位于声明下），如下所示。

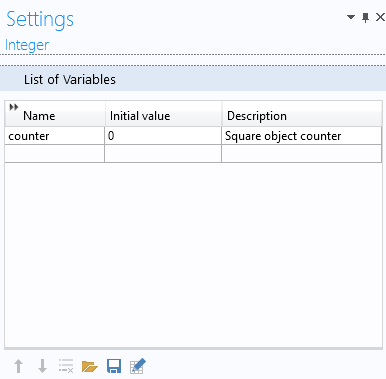
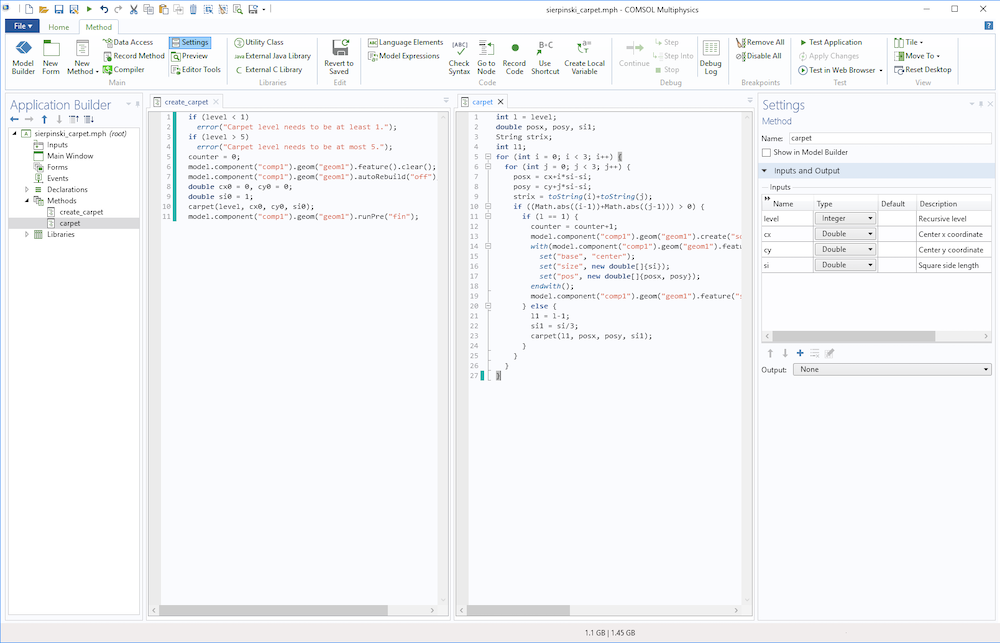
上述两个函数的代码在方法编辑器中并排显示如下：

为了运行 create_carpet，首先将其添加为方法调用。相应的菜单按钮在开发工具 选项卡中可用。

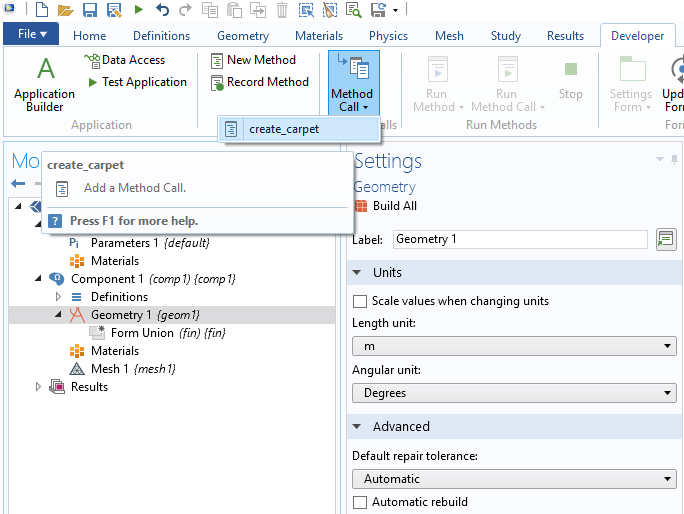
添加后，我们可以更改递归层，并单击运行 按钮。

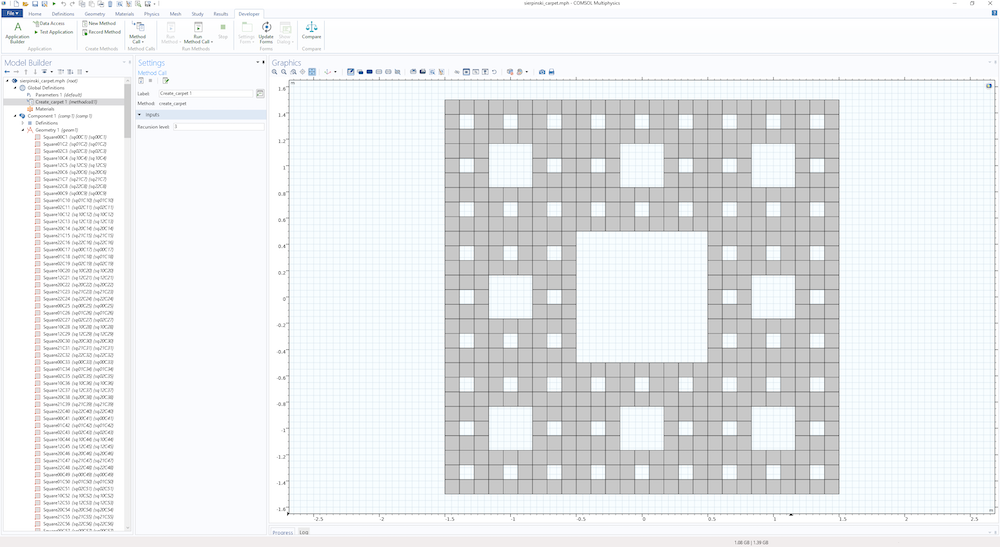
下图显示了设置递归层为3时得到的地毯的最终几何图形。

请注意，为第 3 层地毯定义的方形几何对象数为 512。第 N 层地毯的几何对象数为 8^N。这意味着，使用 create_carpet 方法设置的最大层数 5 ，生成的几何图形有 32,768 个几何对象！如果你想尝试 5 层地毯，请确保你的计算机足够强大！

Menger海绵

前面我们已经讨论了二维递归定义的几何对象，那么三维对象呢？Sierpinski 地毯的三维几何称为 Menger 海绵。Sierpinski 地毯的方法很容易推广到三维。但是，在三维中，我们需要注意不要生成超出计算机处理能力的对象。

使用以下方法 create_sponge 启动递归。

if (level < 1)
  error("Carpet level needs to be at least 1.");
if (level > 5)
  error("Carpet level needs to be at most 5.");

counter = 0;
model.component("comp1").geom("geom1").feature().clear();
model.component("comp1").geom("geom1").autoRebuild("off");
double cx0 = 0, cy0 = 0;
double si0 = 1;
carpet(level, cx0, cy0, si0);
model.component("comp1").geom("geom1").runPre("fin");

由上面的方法调用并递归创建一个 Menger 海绵，得到如下所示的方法海绵。

int l = level;
double posx, posy, si1;
String strix;
int l1;
for (int i = 0; i < 3; i++) {
  for (int j = 0; j < 3; j++) {
    posx = cx+i*si-si;
    posy = cy+j*si-si;
    strix = toString(i)+toString(j);
    if ((Math.abs((i-1))+Math.abs((j-1))) > 0) {
      if (l == 1) {
        counter = counter+1;
        model.component("comp1").geom("geom1").create("sq"+strix+"C"+toString(counter), "Square");
        with(model.component("comp1").geom("geom1").feature("sq"+strix+"C"+toString(counter)));
          set("base", "center");
          set("size", new double[]{si});
          set("pos", new double[]{posx, posy});
        endwith();
        model.component("comp1").geom("geom1").feature("sq"+strix+"C"+toString(counter)).label("Square"+strix+"C"+toString(counter));
      } else {
      l1 = l-1;
      si1 = si/3;
      carpet(l1, posx, posy, si1);
      }
    }
  }
}

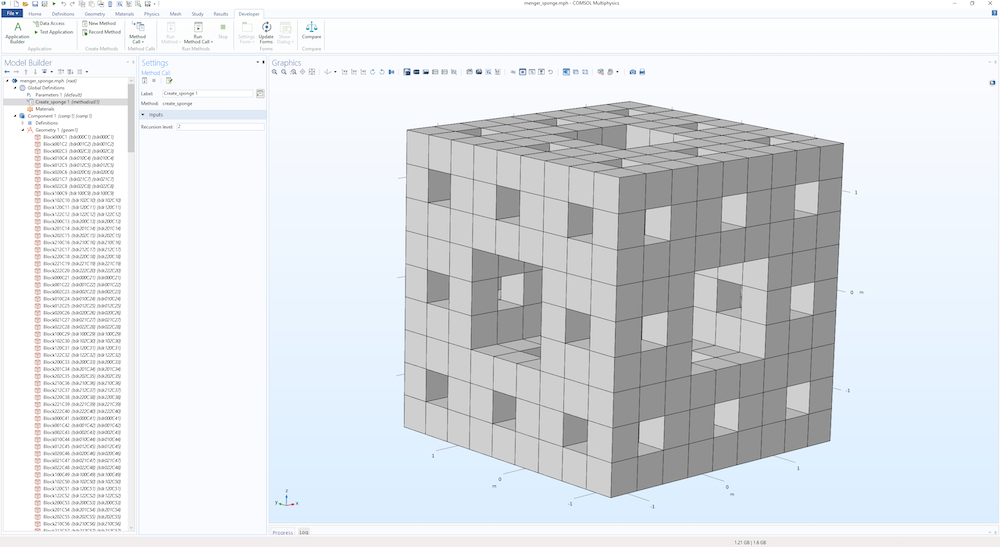
下图显示了 2 层海绵的最终几何形状。

使用这种方法创建的几何对象的数量随着层数 N 增加为 20^N，上面显示的 2 层海绵有 400 个块几何对象。

根据关于创建 Koch 雪花的迭代方法的这篇博客，我们也不可以不是使用递归来创建这种类型的结构。

如果你有任何用于附加的 CAD 功能的附加产品，都可以将这些几何对象导出为标准的 CAD 格式。如果没有附加产品，也可以将网格几何导出为任何支持的网格格式，例如 STL。

下一步

单击下面的按钮进入 COMSOL 案例库，尝试使用本文中介绍的模型。