模拟喇叭中的非线性声传播

当对声学器件建模时，虽然总存在非线性因素，但通常只考虑线性传播就足够了。然而，当在设计中信号幅度达到较高程度时，非线性效应就会显得尤为重要。工程师可以利用 COMSOL Multiphysics® 软件中的非线性声学（Westervelt） 特性，在仿真中加入非线性效应，如指数曲线形喇叭示例所示。

使用声学喇叭增加声音幅度

最古老的扩声方法之一是使用喇叭，其中一个典型的例子便是机械留声机。19世纪70年代，托马斯·爱迪生发明了留声机，该系统由用箔片包裹的木制圆筒（后来用蜡制成）、唱针和放置在箔片或金属膜片上的喇叭构成。

有了留声机，你只需对着喇叭说话就可以录音，声波振动会使唱针在箔片上蚀刻出凹槽。你也可以通过把唱针放在凹槽的始端并转动机器的手柄来听录音。当唱针沿着凹槽纹路移动时，所产生的振动会被喇叭放大。这些性能启发了声学工程师去改进设计，不久，圆筒便被平板唱片取代，并使用更先进的喇叭来改善扩音效果。

左图：托马斯·爱迪生和早期留声机。本图是在美国公开的图片，源自维基共享资源。右图：圆筒旁是一个经典喇叭形的留声机。Tomasz Sienicki -Own work | 图。CC BY-SA 3.0 许可协议授权，源自维基共享资源。

如今，声学喇叭是用于电动扬声器或船舶、火车上发信号的常用元件，但以前，喇叭扬声器不能远距离传播。然而，在这一领域引入电之后，喇叭扬声器可以将低电力转换成高音量，从而满足大型场馆的需要。电动扬声器不再是用机械驱动的膜片，而是使用电磁动圈和膜片产生声音，并通过喇叭将声音放大。这些高效扬声器常用于户外公园或体育场的公共广播系统以及声音报警系统。对于高振幅信号，常用压缩空气驱动器代替电磁电机。

喇叭之所以如此有效，是因为它的形状有利于控制横截面递增。这导致了声源（扬声器）和周围空气之间出现所谓的阻抗匹配，就是说，声学喇叭可以在很大的频率范围内有效地辐射声音。当压力与粒子速度处于同一相位时，就可以获得有效的辐射，这就要求在较低的频率下具有较大的平面。声学喇叭能够实现这种效果：声音是由一个小的声源（位于喇叭喉部）产生的，却通过一个较大的平面（喇叭口部）辐射声音。喇叭的阻抗匹配特性保证了辐射波前的变化尽可能小（从喉部到口部），使压力和粒子速度保持同一相位。Webster 喇叭方程给出了喇叭声学最简单的一维描述。一种常见的喇叭扬声器是指数曲线形喇叭，它具有良好的阻抗匹配性能。

当声学喇叭以非常高的振幅被驱动时——这通常是用于船舶或火车信号传递或用于音乐会场地声音系统的情况——需要考虑声学的非线性行为。由于喇叭的几何形状，高声压级（sound pressure levels， SPL）通常位于喇叭喉部。虽然非线性传播以较低的振幅呈现，但只有达到较高的振幅才能显示出其效果。因此，当使用声学喇叭进行高振幅信号传输时，在仿真中考虑非线性效应这点至关重要。

线性声学适用性判断的经验法则是，只要声压 p远小于\rho c^2（即|p| \ll \rho c^2），这一法则才有效，其中\rho是流体密度（空气密度为1.2 kg/m ³），c是声速（空气中为343 m/s），由此可以得出空气中的数值为\rho c^2 = 1.4 \cdot 10^5pa 。假设“远小于”对应的系数为100，线性声学适用于声压级最高约为154 分贝的情况下。

用 Westervelt 模型建立高振幅声学模型

你可以使用声学模块（COMSOL Multiphysics 的附加产品）对喇叭产生的非线性声传播进行建模。仿真可以让你看到喇叭喉部的输入波形如何影响喇叭口部的输出波形。在这个指数曲线形喇叭的例子中，模型设置为在喇叭喉部以频率为 f₀ = 130Hz的谐波输入信号进行驱动。这就产生了含有 2 f₀、3 f₀ 和 4 f₀ 等谐波频谱的声波。模型网格可求解的最高谐波为四次谐波 4 f₀。非线性声学仿真要求对系统进行完全的非线性瞬态分析，因为频域模型只适用于线性情况。

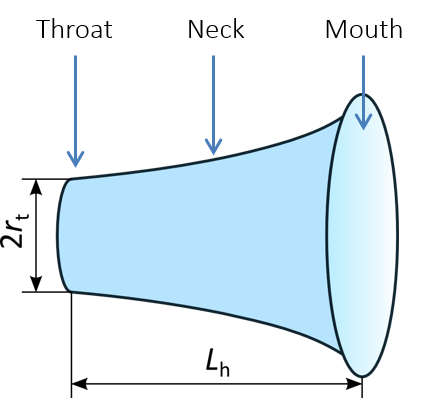
声学喇叭模型示意图。

本例采用压力声学，瞬态 接口为声压进行瞬态计算，而耗散（热传导和粘性）材料模型和非线性声学（Westervelt） 域条件（后者从 COMSOL® 软件5.4版本开始使用）模拟了物理领域下声学的非线性传播。如下图所示的二维轴对称模型，该模型包括外场计算 边界条件（同样也从5.4版本开始使用）, 可用于计算辐射图并将其可视化（稍后将详细介绍），还包括完美匹配层（perfectly matched layers，PML），将其与无损的瞬态压力声学模型节点一同使用，可以此模拟向无限域传播的无反射条件。

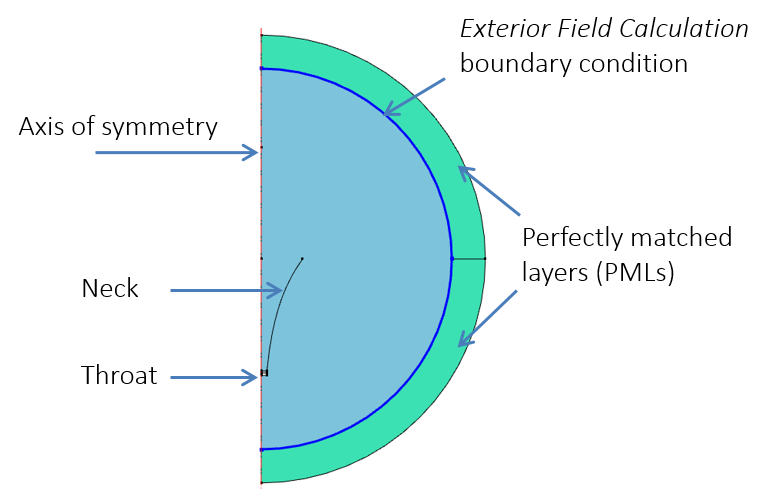
二维轴对称模型设置。

非线性瞬态研究分为两个步骤：

1. 瞬态分析
2. 时域到频域快速傅里叶变换（fast Fourier transform，FFT）

第一步，非线性声学（Westervelt） 特性会对瞬态求解器进行自动调整。这种便捷功能有助于更有效地解决非线性问题。一旦解达到稳定状态，就会执行时域到频域FFT，并将结果存储在外场计算边界上，用于计算外场。

评估仿真结果

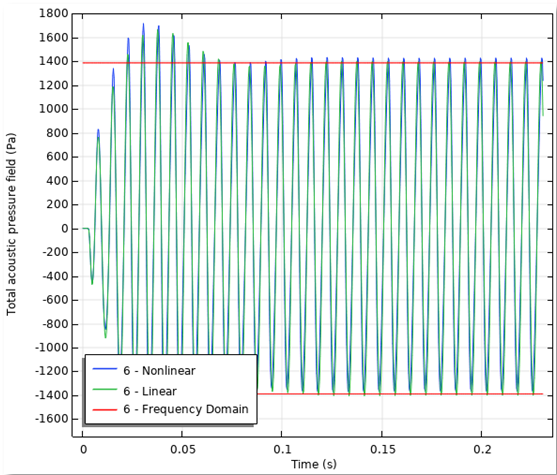
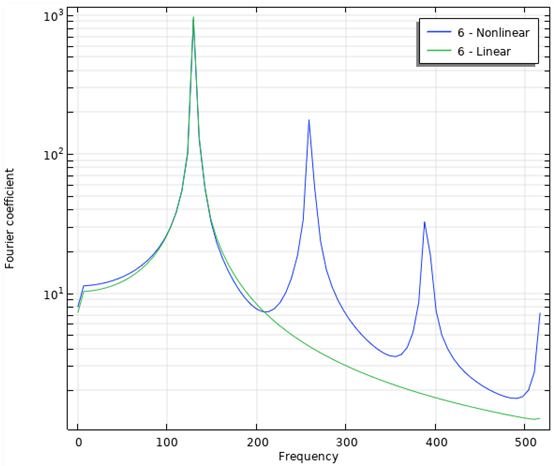
首先可在结果中查看声压。下面左图对比分析了喇叭前方一点处的线性（绿色）和非线性（蓝色）结果。红线对应于根据频域模型计算的振幅。从这个图中，可以直观地看到高振幅下的总体非线性声压。

 

左图是用线性和非线性方法计算声压的对比；右图的动画直观地显示了总体非线性声压分布。

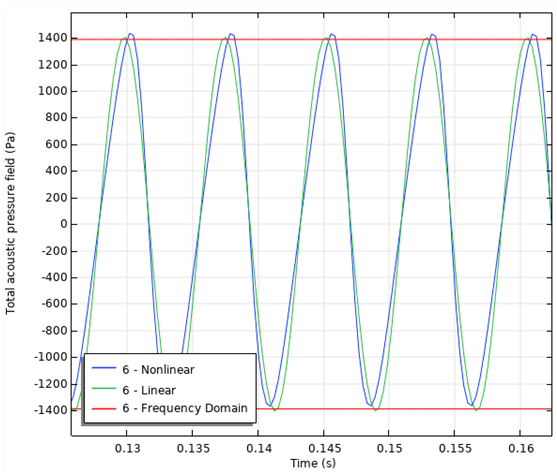
接下来，你可以分析信号的频率信息。左图显示了声压的瞬态计算，放大至5个周期。右图显示了线性和非线性分析的频谱。从图中可以明显看出，非线性模型含有高次谐波分量。由于非线性行为，能量从基频被提取到高次谐波。

声压相对时间的函数（左），含非线性谐波分量的频谱清晰可见（右）。

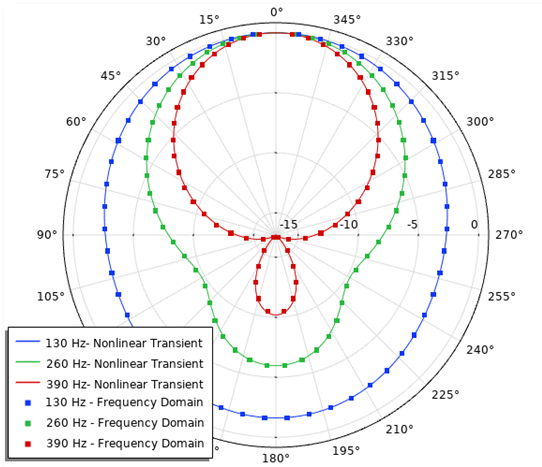
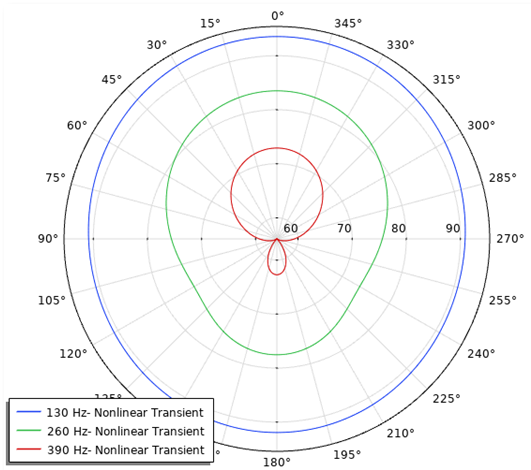
接下来，你可以查看外场部分。外场计算功能可实现对距声源任意距离处的声场辐射进行可视化，从而便于研究外场 SPL。下面左图是归一化的外场 SPL，显示了非线性与单频率分析的对比。右图则可以看到非线性瞬态分析，显示了前三次谐波频率分量的外场 SPL。后一幅图还显示了各个分量的相对振幅。

左图是非线性分析相对于单频域的归一化外场 SPL。右图是前三次谐波频率分量的外场 SPL 的非线性瞬态分析。

指数曲线形喇叭模型中的非线性效应。

如本例所示，非线性声学（Westervelt） 特征和)外场计算 边界条件可实现声学仿真中对非线性传播和影响的考虑并将其可视化，从而使工程师能够对需要更高振幅信号的声学设计进行改进。

下一步

尝试自己建模一个声学喇叭：点击下面的按钮，进入案例库。从中，你可以下载一份逐步建模指南和 MPH 文件（必须先登录到你的 COMSOL Access 帐户并拥有有效的软件许可证）。

更多资源

• 阅读以下博文，从中了解非线性声学仿真：
  • 如何对扬声器驱动器实现非线性失真分析
  • 第2部分：对非线性系统的谐波激励建模
• 准备好进行更多的非线性声学建模了吗？尝试本教程：
  • 非线性声学——一维 Westervelt 方程建模