
声学扩散方程是最快速、最简单的高频声学模拟方法。事实上,当我为父母设计他们的新家时,这一方法对我的帮助很大。在这篇博客中,我将通过亲身体验来介绍声学扩散这一主题,重点讲解这一模拟方法背后的各项假设以及它的优缺点。
个人住所
我父母彼此深爱对方,但他们却有一些极其相悖的生活习惯。我妈妈喜欢看深夜脱口秀,我爸爸则一有机会就想好好睡一觉。当他们最终需要搬到一间较小的房子里时,我决定帮他们好好设计一下房间,让他们还能继续愉快地相处下去。
从过去的经验来看,我知道对绿植、地毯或书架的位置进行优化的意义不大。我爸爸经常会挪动家具的位置,用他的话讲,“感受一下空间”。与此同时,我妈则宁可把沙发搬到尽量靠近电视的地方,也不愿意承认她需要戴眼镜了。
总之,他们一定会搞乱我的输入数据,一个小数点、一个小数点地移走我对噪声水平所做的先验预测的精度。幸运的是,精度并非我的首要考虑。我只要能保证我爸爸睡得好就可以。
在 COMSOL Multiphysics 中模拟声学扩散
要开发一个“临时应急型”的室内声学模型,很显然需要从 声学扩散方程 接口开始。这个接口使用简单,虽然精度略逊于 压力声学 或是 射线声学 接口,但在大多数情况下,它的运算速度要快得多。
我在仿真中简单绘制了所有房间,然后加入大件家具。草图做好后,我开始创建我的第一个声学扩散模型。操作很简单,两个功率源代表连接在电视上的立体声音箱、为墙和家具指定一定的吸收系数……
我们可以轻松在网上找到各种常见材料的近似吸收系数。如果您希望做得更精确一些,还可以针对不同频段使用不同的值,甚至能将它们指定为频率的任意函数。我为墙壁(包含地板及天花板)指定了一个较低的常数值,为家具的软体部分指定了一个较高的值。由于没有加入地毯和其他相对稀疏的装饰物,所以我略微上调了墙壁的吸收系数来弥补这一损耗。如果您打算采用这一类似的省时方法,我建议您能坦率说明这一方法的局限。我父母理解声学扩散并非一门精确的科学,他们也很欣赏我的坦率。
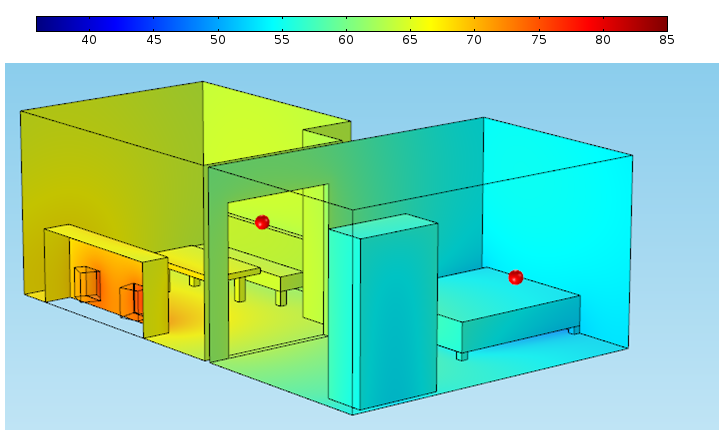
两个房间之间没装门时的声压级 (dB) 分布。红色的点表示我妈看电视的位置,另一个表示我爸睡觉时头部的位置。
门和直达声
在我的第一个解决方案中,客厅沙发和卧室间的声压级只下降了 11 dB。幸运的是,我还没加入两个能帮助增大这一差值的重要因素。
首先是房间的门。如果门的制造商给出了传输损耗 (dB),请务必确认这是仅针对透过门本身的传输,还是对安装在门框中的门进行测量得出的数据。由于大量的声音会透过门与地板之间的缝隙传过,因此除非安装相关配件,二者之间会有差异。如果您能看到门的图纸,了解它的制造材料,那自然可以进行声-结构耦合分析来得到第二个选项。在声学扩散仿真中加入门的具体传输损耗非常重要。
第二个因素是直达声。声学扩散方程只会处理已撞击到墙壁或家具、并因此变得发散的部分声音。我妈妈会直接坐在电视机前,因此也会有大量的直达声传到她身上。通过将声源近似为点,并忽略桌子的阴影区,我们可以轻松地通过声发射能量和局部坐标的解析表达式的方式加入直达声。
在我的第二个(也是最后一个)仿真中,我增加了撞击在沙发上的直达声,并在房间之间加上了一扇门。沙发和床之间的声压差现在已经达到 23 dB,这是一个较能接受的值。我给我父母提供了一份很漂亮的报告,然后同意他们正式搬到新家。
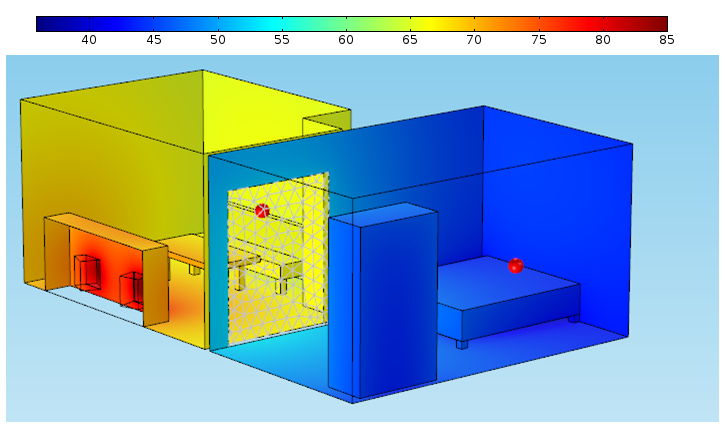
加装门后的声压级 (dB) 分布,以及客厅中直达声的近似。
声学扩散方程
我们更常在描述气体中的粒子运动时提到扩散。除了在随机的时间间隔与气体粒子发生碰撞并反弹外,粒子会沿直线传播。扩散系数是连续两次碰撞之间的平均自由程的函数。

室内气体(左)与声粒子(右)之间碰撞的平均自由程。
声学扩散方程建立在“声粒子”的概念之上,粒子密度与声能量成正比。这些粒子不会在空气分子上发生碰撞,但会在室内的墙壁处发生反弹。平均自由程 \lambda 和扩散系数 D 与房间尺寸相关。它假定 \lambda = 4V/S,其中 V 是房间体积,S 是室内墙壁、地板和天花板的总表面积。此外,D=\lambda c/3,其中 c 是声速。
COMSOL Multiphysics 中声学扩散方程为:
根据方程求解得到的声能量密度 w ,您可以推导出声压级和其他重要的测量指标。如果去掉时间导数,您将得到解的稳态形式。体吸收系数 m_a 用于表征空气损耗,虽然在大部分情况下我们可以忽略这一项,但当空间非常大时它的影响也很大。D_t = D 是扩散系数,q 是体声源。声扩散方程的另一种形式为:
这个方程可以加入对家具的均化描述。式中,\alpha_f 是家具(装饰)的平均吸收系数。扩散系数 D_f 和平均自由程 \lambda_f 由家具的数密度和平均截面积得到。
举个例子,假设我父母曾希望投资一个家具店,那我就会使用这一公式,而非在几何上画出每一个家具。
边界条件提供了各种指定局部吸收系数及声源的方式。我们还可以选择点源。
声学扩散的优点及缺点
同射线声学类似,声学扩散方程不涉及低频行为,比如驻波或拐角处的衍射。这些项对于低于施罗德频率的问题非常重要,您可以在”利用 COMSOL Multiphysics 模拟室内声学“博客中了解更多相关信息。在我父母的新客厅和卧室中,施罗德频率分别是 167 Hz 和 183 Hz。
如果您希望从具体事件得出统计数据,那么将需要对系统进行持续监控。与射线声学相比,声学扩散方程最大的局限是它没有加入早期声音。也就是说,声学扩散方程会系统地低估声源附近的声压级,在本例中,我妈妈在电视机前看电视位置就是这种情况。您可以采用我的方法,对直达声进行解析计算并将它增加到扩散解,这样通常能部分弥补这一缺陷。但如果声源附近的障碍物会对声音产生反射或吸收,这样做的难度将很高,或者说完全无法实现。
也许会有人说声学扩散是 COMSOL Multiphysics 提供的三种声学分析方法中最不精确的一个,但它更容易设定,而且求解速度要比其他方法快几个量级。使用普通台式机,你大约会在经过 2.5 s 的求解后得到本博客所示的结果图。对于包含大量射线的射线追踪模型,您将需要进行几分钟甚至几小时的求解才能获得较好的结果。对于低频且主要为共振的问题,压力声学会是唯一选择。但该方法不适用于远高于施罗德频率的频率问题,因为它会极大地延长求解时间及增加内存使用。
最后,如果您的父母问起您对他们住处声音环境的看法,我强烈推荐您也为他们运行一次声学扩散仿真。此外,如果您正在为音乐厅或办公室做早期设计,将能通过声扩散这一强大的工具对高频声分布进行初步判断。您可以增加射线声学来预测早期声音,从而得出一个更精确的结果;还可以增加压力声学来分析低频行为。
教程下载
您可以点击此处下载本篇博客所介绍的仿真模型。如希望了解室内声学的更多相关信息,建议您前往“案例下载”页面下载家庭住宅声学分析模型教程。






评论 (0)