
等离子体具有高电离度和低电离度、高压和低压、高温和低温等多种不同的特性。对于不同类型的等离子体,需要使用不同的方程和方法模拟。这篇博客,我们概述了不同类型的等离子体,并介绍了如何使用 COMSOL 等离子体模块中的功能来模拟不同的等离子体。
编者注:这篇博客于 2021 年 9 月 17 日更新,以反映 6.0 版本软件接口名称的变化和新功能。
热力学平衡(TE)
如果等离子体处于一个封闭系统中,那么每个过程都与它的逆过程(细致平衡)处于平衡状态,并且等离子体处于热力学平衡状态。这种等离子体可以用几个参数来表征:每一种物质的温度(通常非常高)、压力和数量密度。这种状态下的辐射是黑体辐射,可以用普朗克定律来描述。激发态类物质可以用玻尔兹曼分布描述,速度分布可以用麦克斯韦方程描述,电离度由萨哈方程描述。
局部热力学平衡(LTE)
在真实的等离子体中,会发生偏离平衡的情况。例如,辐射从等离子体中逸出,从而扰乱细致平衡。如果从局部来看,平衡仍然成立,等离子体处于局部热力学平衡状态。等离子体仍然可以用上述关系(在局部范围内)描述,但普朗克定律除外。只有在辐射过程可以忽略不计,并且由碰撞产生的等离子体占主导时,才存在局部热力学平衡。因此,需要足够高的电子密度。
部分局部热力学平衡(PLTE)
由于电子的质量明显低于重物质,因此更容易受到电场的影响,从而在单位时间内获得的能量比重物质多。如果压力低或电子密度小,重物质的温度将低于电子的温度。此时,等离子体就不能再用单一的温度来描述了。
基态和第一激发态之间的能量差通常很大,但激发态之间的能量差很小,尤其是在惰性气体中。如果电子密度足够高,激发态之间可以处于平衡状态(不包括基态)。尽管不同的物质具有不同的温度,但它们的速度分布仍然可以用麦克斯韦分布描述。这种情况下,等离子体处于部分局部热力学平衡。
非平衡等离子体
在非平衡等离子体中,重物质温度远低于电子温度。电子和离子所处的背景气体温度接近室温,与平衡状态存在相当大的偏差。因此在这种情况下,上述所有关系都不再有效,需要采取更详尽的描述方法。
我需要使用哪个接口进行等离子体仿真?
COMSOL 等离子模块包括多种不同的接口。下图为展开的等离子体节点屏幕截图,展示了等离子体节点的各个接口:

热等离子体
平衡放电接口适用于模拟热等离子体。这类等离子体可以被看作是导电流体混合物,因此可以使用磁流体动力学(MHD)方程描述。磁流体动力学结合了纳维-斯托克斯方程、热方程和麦克斯韦方程组来描述电磁场中导电流体的运动。模拟中忽略了等离子体的化学成分。
下图显示了电感耦合等离子体炬的模型开发器。在这个模型中,磁场 接口用于求解安培定律,传热 接口用于求解能量平衡方程,层流 接口用于求解纳维-斯托克斯方程。此外,还有一个多物理场节点用于耦合不同的接口。
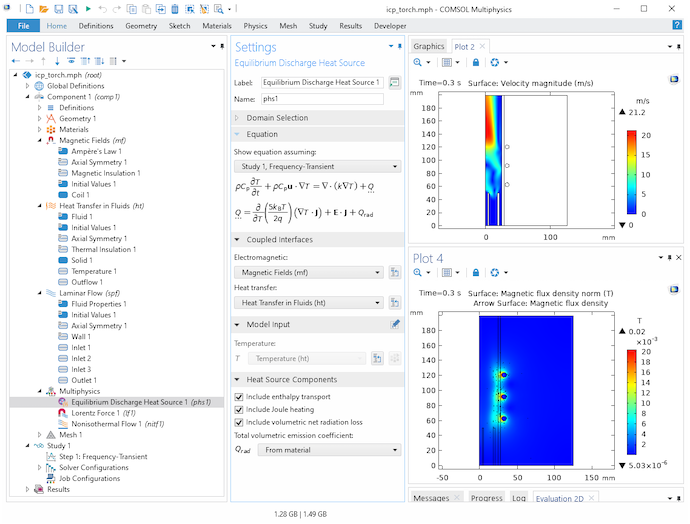
电感耦合等离子体炬模型的模型开发器,突出显示了 平衡放电热源 耦合的设置。
平衡放电 接口假设等离子体完全电离,并且等离子体处于局部热力学平衡条件。
平衡直流放电 接口用于研究由静电场或缓慢变化的电场维持的平衡放电,其中忽略了感应电流和流体流动效应。
平衡电感耦合等离子体 接口用于研究感应电流维持的平衡放电,例如电感耦合等离子体炬。
电感/直流耦合放电 接口用于研究由感应电流和(或)静电场(或缓慢变化的电场)维持的平衡放电,例如电弧焊模拟。
非热等离子体
其他接口适用于模拟非热或非平衡等离子体。这里以一个使用漂移扩散近似的流体模型来说明。该模型求解了物质的质量守恒方程、电子的能量平衡方程和电场的泊松方程。在这个示例中,等离子体化学是模型的重要组成部分。模型还求解了麦克斯韦方程组以考虑与磁场或电磁波的耦合。
下图为软件内置的电感耦合非平衡氩等离子体的模型开发器的屏幕截图。您也可以在COMSOL 案例库中找到此模型。在这个模型中,等离子体 接口用于模拟(通过漂移扩散近似的)电子和重物质传递之间的复杂相互作用和静电场。您还可以看到用于描述等离子体化学的节点。磁场 接口用于求解安培定律,模拟线圈的电磁场。此外,还有一个多物理场节点可用于考虑上述接口的耦合。
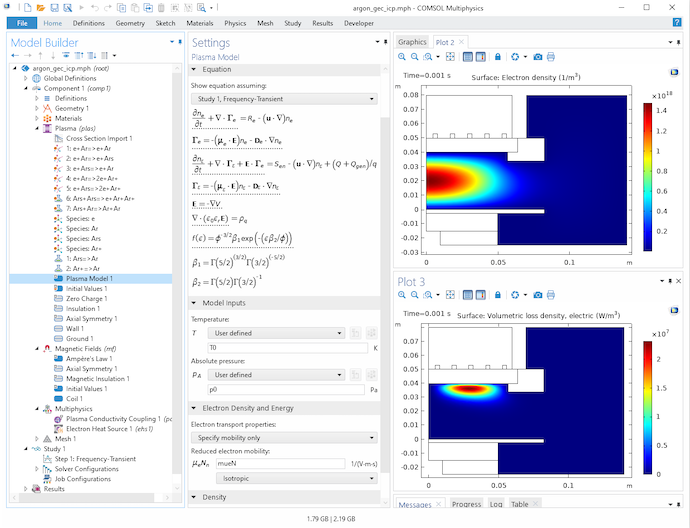
电感耦合氩等离子体 GEC 反应堆模型开发器,突出显示了等离子体模型的设置。
等离子体 接口用于研究由静电场维持的放电。等离子体,时间周期 接口用于研究由时变静电场维持的电容耦合放电。电感耦合等离子体 接口用于研究感应电流维持的放电。 微波等离子体 接口适用于研究由电磁波维持的放电(波加热放电)。 电晕放电 和 电击穿检测 接口在工程上可分别用于快速计算电晕和流柱放电是否发生。
推荐资源
- 查看案例下载页面,下载等离子体仿真教程模型
- 观看视频,了解等离子模块的主要特征
- 如果您在仿真过程中遇到任何问题,欢迎联系 COMSOL 技术支持






评论 (0)