通过仿真理解经典灰体辐射理论

虽然热辐射效应早就被应用在第一个人造光源中，但直到量子力学的发现，这种效应才被完全理解。如今，这已经是一个众所周知的物理学概念了。在这篇博文中，我们将讨论灰体的表面对表面辐射理论，了解如何在 COMSOL Multiphysics^® 软件中实现，以及该理论的有趣用途。

经典热辐射理论

烛光是第一个人造光源，之后过了很久，煤气灯才出现，然后到 19 世纪，人类发明了第一盏电白炽灯。140 年后，白炽灯正在被 LED 取代。

蜡烛、煤气灯和白炽灯全都应用了热辐射理论，即在没有导热介质存在的情况下唯一的热传递现象。如果没有这一特殊物理特性，人类将无法在地球上生活：因为太阳能通过辐射穿过真空进入地球。

一个白炽灯泡。

物理学中最有趣的故事之一是马克斯·普朗克发现了黑体辐射的光谱分布公式，现在称为普朗克分布。黑体 是一个理想化的物理体，它能吸收 所有 入射电磁辐射，同样也能发出最大热辐射。

黑体理论的发现打开了量子力学的大门。通过普朗克的工作，现在我们知道了能从处于平衡状态的、温度为 T 的黑体中能获得多少能量，这被称为 斯蒂芬-玻尔兹曼定律：

其中，\sigma \simeq 5.67 \times 10^{-8} \; \; \; (W/m^2 \cdot K^4) 是斯蒂芬-玻尔兹曼常数，n 是介质的折射率。

现在我们考虑更贴近实际的物体——灰体。灰体是不完美的黑体，即部分 吸收入射电磁辐射的物理体。相同温度下灰体的热辐射与黑体的热辐射之比称为灰体的发射率。

黑体的发射率是均一的，而灰体的发射率大于 0，小于 1。发射率是辐射表面的几何形状、物理属性和波长的函数。那么对于一些特定结构，如何确定其发射率呢？

为简单起见，本节我们将以漫反射灰体表面为例来说明，不考虑辐射的光谱依赖性。以下理论基于 Gouffé 的论文(参考文献 1)，该论文概述了经典的灰体辐射理论。该理论中的数学知识你可能在中学或高中时学过，但物理概念要复杂一些。Gouffé 的论文发表后被许多研究人员引用（参考文献 7）过。在这篇博文中，我们将尝试对原始论文中缺少的内容进行补充研究，以便提供完整的解释。

首先，定义我们需要用到的术语和约定。当我们在这篇博文中提到 反射率 和 吸收率 时，我们必须区分是“材料”量还“表观”量，避免在学习热辐射时产生混淆。由于灰体表面通常具有某些（微小）结构，因此从远场观察到的“表观”量与原材料量不同。例如，粗糙表面的表观反射率总是低于其材料反射率。

我们的目标是根据给定的材料反射率和结构的几何形状计算表观发射率。本文中，我们将通过在“材料”量的符号中附加“_0” 来与“表观”量相区分。如果没有此符号，就可以理解为我们讨论的是一般的量。术语的命名如下：

• 材料反射率，\rho_0
• 材料吸收率，\alpha_0
• 材料发射率，\varepsilon_0
• 表观反射率，\rho
• 表观吸收率，\alpha
• 表观发射率，\varepsilon
• 腔体内部面积，S
• 开放面积，A
• 视角，\theta
• 角系数(归一化立体角)，F
• 角系数(面积比)，G

根据能量守恒定律，对于不透明材料的反射率 \rho 和吸收率 \alpha，存在以下关系：

基尔霍夫定律指出，材料的发射率 \varepsilon 在热力学平衡时等于吸收率 \alpha，即

从上面的两个关系，我们可以从反射率得到发射率，即，

考虑一个单一的表面结构，如下图所示。这可以是任何结构，本篇博文中，我们使用了一个球形腔体。在腔体顶部有一个面积为 A（半径为 R 的圆)的开口，开口与腔体底部的距离为 \rho_0。假设材料反射率 \rho_0 在腔体内表面上是均匀的，并且反射服从朗伯定律，即，反射的强度是 I_r = \rho_0 \cos \theta，其中\theta 是视角，如下图所示。我们想要计算一束入射的单位能量光有多少表面反射。

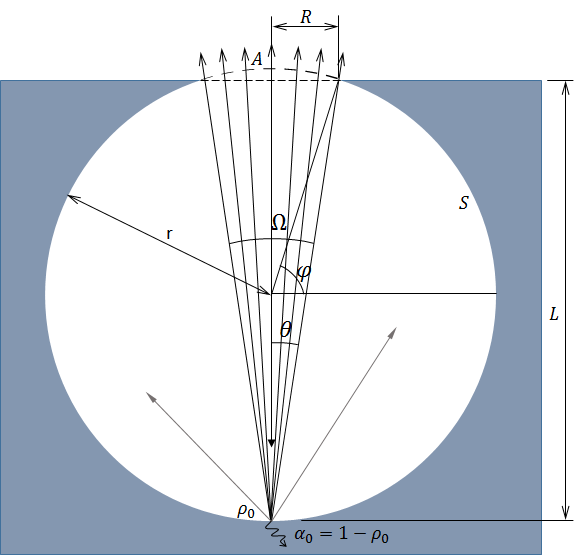
用于计算表观反射率的表面结构。

作为一阶近似，腔底部的反射为：

其中，F 称为角系数。

请注意，在 Gouffé 的论文中，假设角系数在腔体表面上是均匀的。在 COMSOL^®软件中，它是位置的函数，这始终是正确的。（因此，我们需要积分来计算发射率。）

这里，角系数是从第一反射点到开口的归一化立体角。立体角 \Omega 通过下列公式计算：

请注意，半球的总立体角为 \pi，而不是 2\pi，这是由于朗伯因子为 \cos \theta。

角系数 F 的结果为

对于这个近似值，表观反射率是

由此推导出表观发射率为

粗略来说，开口越小，腔体越接近于黑体，这是由于角系数的原因。

接下来，我们对近似值进行改进。在计算过第一次反射之后，其余部分被腔体材料吸收或进一步反射。材料吸收 \alpha_0 根据能量守恒为 \alpha_0=1-\rho_0。剩余能量为后续反射：

现在，再次假设进一步的反射以 均匀 的方式发生，在第二次反射时从腔体中出来的反射应该是上述量再次乘以材料反射率和另一个角系数，这个角系数由面积比 G= A/S 定义，S 是空腔的面积，包括开口面积 A。第二次反射的表观反射率为

与一阶近似类似，二阶近似的表观发射率为：

对于这个近似值，带附加项的表观发射率应该更加准确。

最后，我们可以通过计算以下收敛无穷级数来考虑所有反射：

对于球体，可以证明 F=G，这可以将结果简化为

根据几何参数 R 和 L，我们可以重写 F 和 G。在几何上很容易证明 \sin \theta = R/\sqrt{L^2+R^2}，由此 F 可以改写为

开口处的面积 A，可以通过下式计算

其中，r 是球体的半径，\varphi 是过球心的平面的角度，该平面与开口周长平行。

从几何学来看，存在关系 R^2+(L-r)^2= r^2，可以得到和 r=(R^2+L^2)/(2L) and \cos \varphi = R/r。通过使用这些关系，开口面积 A 可以改写为

由于球体总面积为 S=4\pi r^2,, 角系数 G 可以写为

这证明了 F=G。

请注意，在 COMSOL^® 软件中，我们没有角系数 F, 只有一个纯几何量的角系数 G。

COMSOL Multiphysics^® 仿真与理论比较

到目前为止，我们已经学习了经典的灰体理论。现在，我们使用表面对表面辐射传热 接口来计算最终目标，即由带开口的球壳组成的灰体的表观发射率。然后，我们可以将计算得出的开口尺寸对发射率的依赖性与近似公式进行比较。

在查看主要结果之前，让我们检查一件事。在 COMSOL Multiphysics 中，我们可以使用 radopu 和 radopd 算子计算角系数值（对应于上述理论中的 G，但其是位置的函数）。使用这些运算对象得到的量是纯几何的，所以使用这个算子不需要运行研究。如果您更改了几何图形，可以在使用算子之前更新解。

在这个模型中，只有一个辐射面，因为该模型是一个开放的腔体。因此，COMSOL Multiphysics 只能计算腔体表面 本身 的角系数。我们将其称为自身角系数。到目前为止，我们讨论的角系数，是指从腔体表面上的一点观察腔外部的系数，可以称为 环境角系数。我们可以通过从整体中减去自身角系数来计算角系数，即 1-intop1(comp1.ht.radopu(1,0))/intop1(1)。

就像我们前面讲过的，角系数通常取决于位置，COMSOL^® 软件中的角系数也是如此。为了计算腔体表面上所有点的贡献，我们需要将角系数对位置做积分。 intop1 算子是定义在腔体表面上的积分算子。下图将计算结果与经典角系数理论进行对比，吻合度非常好。

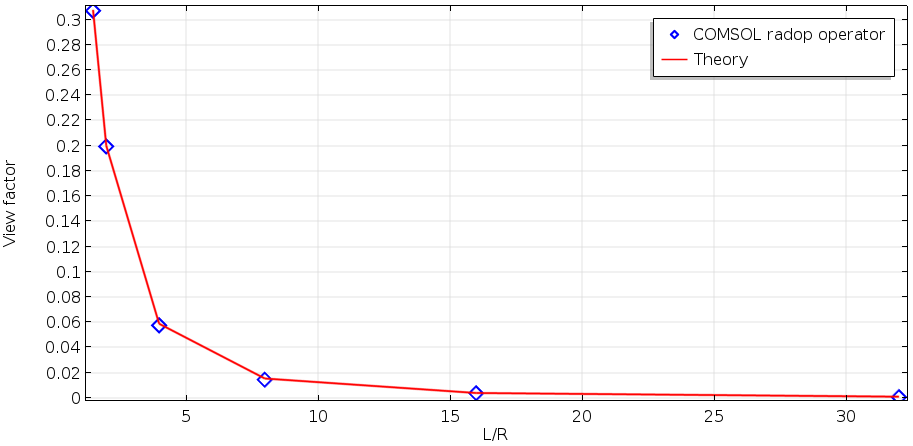
经典理论与使用 COMSOL Multiphysics 中的 radopu 算子计算的环境角系数的比较。

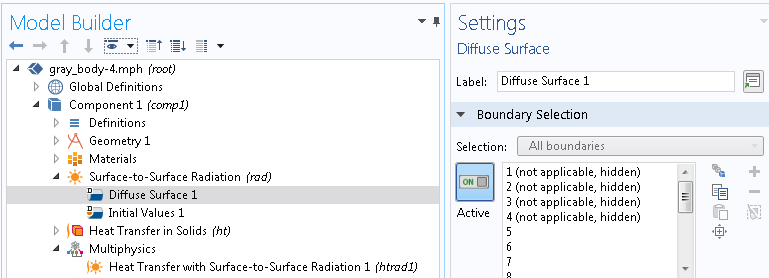
现在，让我们继续进行设置。要计算表面对表面辐射，需要添加表面对表面辐射 物理场接口，为球体的内表面添加一个漫反射表面 节点，然后再添加一个表面对表面辐射传热 多场耦合节点(见下文)。COMSOL Multiphysics 将对每个网格节点执行表面积分来计算角系数，使用封闭表达式的轴对称几何除外。为简单起见，我们不包括环境辐射，即 T_{\rm amb}=0。温度 边界条件设置为球壳的外边界 T_0= 2500 deg K。材料发射率设置为 0.5，以便更容易地看到差异。

漫反射表面节点的设置。

下图显示了针对各种开口半径计算得出的环境角系数、辐射度和温度。根据 Gouffé 的论文，将几何纵横比定义为 L/R，用作扫掠参数，R 是开口的半径，L 是空腔高度。

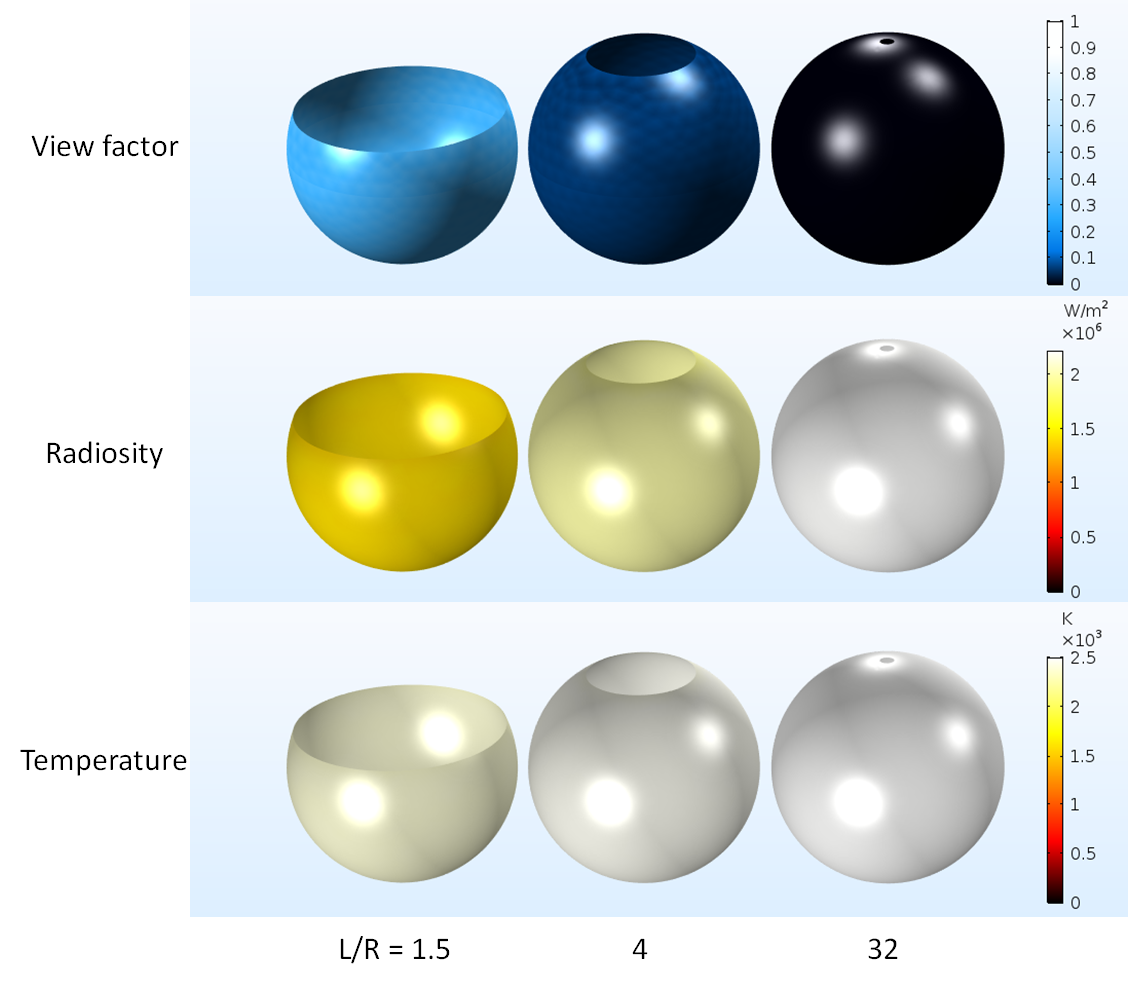
计算出的角系数、辐射度和温度与 L/R 的比较.

这些结果定性地表明，开口尺寸越小，腔体发出的热辐射越多，表面温度越高。

为了计算辐射度的表观发射率，我们现在可以使用斯蒂芬-玻尔兹曼定律。黑体在温度 T_0 下的辐射度是 \sigma T_0^4。将计算的辐射度除以这个数字，我们可以得到灰体球腔的表观辐射率，即 intop1(ht.J)/intop1(1)/(sigma_const*T0^4)。现在，我们将结果与我们迄今为止讨论的各种理论进行比较。

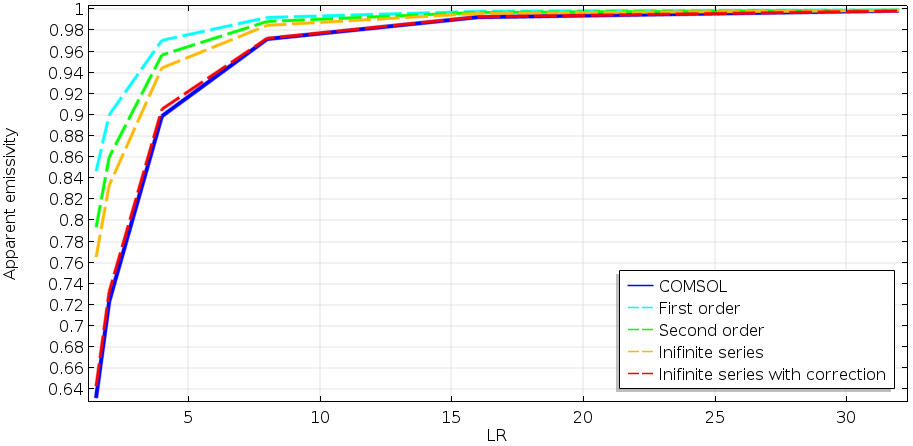
球形腔体表观发射率的各种理论近似值与COMSOL Multiphysics 计算结果之间的比较。

青色线表示一阶近似值，它低估了反射，造成更高发射率，这个结果是不准确的。二阶近似值明显提高了准确率，但还不够准确。无限阶近似绘图（橙色线）给出了更好的结果，但仍与 COMSOL Multiphysics 的结果不太接近。

Gouffé 论文的最后一部分提到了导致这种差异的原因。正如一些读者可能已经注意到，上图中每个几何形状的表面温度都不同，尽管外部的边界温度相同，为 2500 K。这称为辐射冷却。我们还没有包括这种效应，它发生在任何具有有限热导率的真实材料上。辐射冷却效应会改变外壳温度的内表面温度，具体取决于开口面积。因此，需要对温度进行补偿，以计算所有开口区域在相同温度下的发射率。

由于斯蒂芬-玻尔兹曼定律，修正系数为温度比的四次方；即，(maxop1(T))^4/T0^4，其中 maxop1 是定义在腔体表面上的算子，用于寻找表面上的最大值。最后，通过这一修正，红色曲线是最准确的理论预测，这与 COMSOL Multiphysics 的结果（蓝线）非常吻合。

使用 COMSOL^® 软件设计高效白炽灯

白炽灯的光源是由一个扭曲的钨丝制成的。在 0.467 微米波长下，钨的材料发射率在 2500K 时为 0.462（参考文献2）。过去，研究人员提出，如果我们在钨丝表面制造一些微结构，就可以设计出更高效的白炽灯。这是真的。正如我们刚刚了解到的，如果我们有一个带有非常小的开口的空腔，我们可以将其称为黑体灯丝，则表观发射率可以接近 1。此外，研究（参考文献3-4、8-9) 还提出，如果最大腔体尺寸约为 0.78um 的一半，那么任何波长大于 0.78um 的红外光都可能由于波导的截止效应而被抑制。那么，可以显着提高可见光的效率。

这种影响可能不仅仅是发射率的提高，因为低于钨熔化温度的辐射主要由红外光组成的会浪费在加热上。如果我们真的能切断红外线，那就太棒了。

我们带有红外抑制黑体灯丝的“梦想”白炽灯。图片来自 Wikimedia Commons 公共领域。

遗憾的是，由于种种原因，这盏“梦灯”无法成为现实。

首先，表面不可能都是孔。要制作角系数低的孔，意味着开口面积小于孔尺寸，表面不能密集地填充开口，即开口之间的表面需要有一个更平坦的区域，从而辐射红外线。或者，我们可以制作深孔以降低环境角系数，然后让每个孔尽可能地靠近相邻的孔。然而，更深的孔使得制造变得更加困难。

此外，带孔的表面的表面能似乎高于平坦表面的表面能。因此，带孔的表面倾向于在低于整体熔化温度的温度下熔化。

第三，在双绞线灯丝上打孔非常困难，因为它是三维结构。在扁平带状灯丝上打孔更容易，因为它是二维的，但扁平灯丝在电气上并不方便，因为它们需要比绞线灯丝更多的电流才能达到相同的温度，而不是扭曲的线状灯丝（更高的电压和更低的电流对我们目前的基础设施来说更方便）。

结束语

虽然灰体辐射理论是在很早以前提出的，但该理论已经非常完善了。解析角系数公式有很多来源（参考文献5；请注意，它也被称为“配置因子”）。这个理论已经被实验证明，并且适用于许多现实世界的应用，但它似乎太难理解了。在这篇博文中，我们学习了一个最简单示例的理论，并通过 COMSOL Multiphysics 仿真得到了非常成功的基准测试结果。COMSOL 软件内置的表面对表面辐射传热 接口是一种可靠的工具，可以使复杂的辐射计算变得更容易。

通过制作特殊的角系数，我们可以设计出更有趣的白炽灯。如果我们在扁平带状灯丝上制作微小的周期性凹槽，将绘得到一个“定向”白炽灯。通常，灯丝向所有方向发射光，但这种特殊的灯丝只照亮某个方向（参考文献6）。我们可以通过仿真探索灰体辐射理论的更多想法和更多应用。

下一步

单击下面按钮，进入 COMSOL^® 案例库，您可以下载相关的 MPH 文件，尝试自己动手模拟灰体模型。

参考文献

1. A. Gouffé, “Corrections d’ouverture des corps-noirs artificiels compte tenu des diffusions multiples internes (Corrections of emissivity for the artificial black-body considering multiple internal diffusions)” (in French), Revue d’Optique, t. 24, no. 1–3, 1945.
2. C.J. Smithells, Tungsten, Chapman & Hall, Ltd., 1926.
3. J.F. Waymouth, Proceedings of LS-5, 1989.
4. J.F. Waymouth, J. Illum. Engng. Inst. Jpn., 74, 12, pp. 800–805, 1990.
5. J.R. Howell, “A Catalog of Radiation Heat Transfer Configuration Factors“, University of Texas at Austin.
6. W.Z. Black, “Radiative heat transfer characteristics of specially prepared V-groove cavities”, PhD Thesis to Purdue University, 1968.
7. Precision Measurement and Calibration, Radiometry and Photometry (Vol. 7), U.S. Department of Commerce, National Bureau of Standards.
8. M. Sugimoto, T. Fujioka, T. Inoue, H. Fukushima, Y. Mizuyama, S. Ukegawa, T. Matsushima, and M. Toho, “The Infrared Suppression in the Incandescent Light from a Surface with Submicron Holes”, Journal of Light & Visual Environment, Vol. 18, No. 2 (1994).
9. T. Kondo, S. Hasegawa, T. Yanagishita, N. Kimura, T. Toyonaga, and H. Masuda, “Control of thermal radiation in metal hole array structures formed by anisotropic anodic etching of Al”, Optics Express Vol. 26 No. 21 (2018).