Menu
COMSOL 博客

借助虚构解方法验证仿真

Author Image
作者 Temesgen Kindo
2015年 7月 27日

我们该如何检验仿真工具是否正确工作？方法之一就是虚构解方法。该方法涉及假设一个解，获取与假设一致的源项及其他附加条件，使用上述条件作为模拟工具的输入项来求解问题，以及对比结果与假设解。该方法使用简单且用途广泛。例如，桑迪亚国家实验室的研究人员将该方法与一些内部代码一同使用。

验证与确认

对于一些无法预见的情况，使用数值模拟工具预测结果前，我们希望保证该方法的可靠性。为此我们可以检查模拟工具是否准确复现了已有的解析解，或者结果是否与实验观察相符。这就带来了两个紧密相关的主题：验证与确认。我们将在博客中解释这两项在数值模拟中的含义。

对一个物理问题进行数值模拟，需要两个步骤：

  1. 为物理系统建立数学模型。在此我们需考虑会影响观察行为（输出）的所有因素（输入），并假定控制方程。结果通常为一组输入和输出之间的隐式关系式。这往往会是一个包含初始值和边界条件的偏微分方程组，亦称为初边值问题 (IBVP)。
  2. 求解数学模型，得到以输入显示函数表示的输出。但在实际操作中，这样的闭式解在大多数问题中并不存在。因此我们使用数值法来获取近似解，并需要计算机的配合来求解大型非线性代数方程组和不等式组。

误差常常出现在两种情况下。首先它们出现在数学模型中。忽视一项重要的因素或是假设变量之间的非物理关系都可能造成误差。确认是确保建立数学模型时此类误差不会被引入的过程。而验证则是确定数学模型被准确地求解。在此，我们需确保数值算法可以收敛且计算机能正确执行，从而得到准确的数值解。

简而言之，在确认过程中我们希望知道是否使用了合适的数学模型来描述物理系统，而在验证过程中，我们将检验是否从数学模型中得出了准确的数值解。

确认及验证对比图。
确认和验证过程的对比。

现在，我们将更深入地研究初始边界值问题 (IBVP) 数值解的验证。

各种验证方法

我们该如何检验一个模拟工具是否准确地求解了 IBVP 问题？

一 种可能是选择一个有严格解析解的问题，并以该严格解为基准。例如，分离变量法可用于求解简单的 IBVP 问题。但该方法的限制之一是，大多数实际问题不存在严格解，这也是计算机模拟存在的理由。尽管如此，该方法还 是可以用于算法和编程的完整性检查。

另一种方法是对比模拟结果和实验数据。准确地说，就是将确认和验证合并在一个步骤中，有时也被称为授权。由于数学模型不完善、算法错误或编程中的漏洞得出的错误解与实验观察匹配的概率非常低，除这种小概率事件以外，数值解和实验观察的良好匹配将保证数学模型的有效性以及求解过程的真实性。

COMSOL Multiphysics 的 App 库包含许多用到了上述一种或两种方法的验证模型，并按物理领域进行了分类。

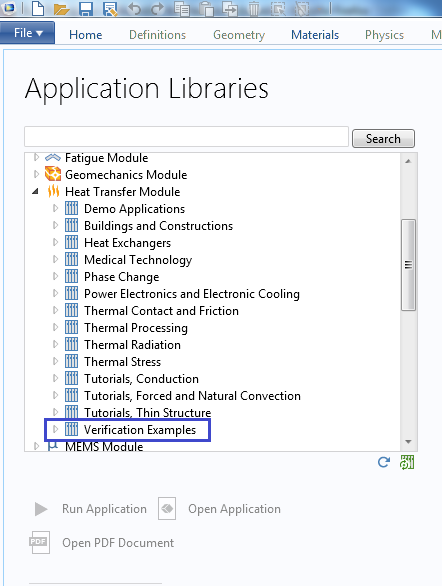
访问 COMSOL Multiphysics 的验证模型。
验证模型可在 COMSOL Multiphysics 的 App 库中找到。

如果没有精确的数学解和实验数据，那该如何验证结果呢？我们可以使用虚构解方法。

执行虚构解方法

求解 IBVP 问题的目标是通过独立变量（通常为空间和时间）、已知问题参数（例如材料属性、边界条件、初始条件以及源项）得到解的显式表达式。源项的常见形式包括体积力（例如结构力学和流体流动问题中的重力）、传递问题中的反应项以及传热问题中的热源。

在虚构解方法 (MMS) 中，我们首先假设解的显式表达式。然后将解代入微分方程并得到源项、初始条件以及边界条件的协调集。这通常需要计算许多导数值。我们接下来将介绍如何在这 一过程中使用 COMSOL Multiphysics 中的符号代数例程。同样，我们在时间 t = 0 时和边界处对假设解求值，从而得到初始条件和边界条件。

接下来是验证环节。刚得到的源项和附加条件作为已知项，使用仿真工具得到 IBVP 问题的一个数值解，并与原始假设解进行对比。

让我们用一个简单示例来解释该步骤。

验证一维传热

考虑一个长度为 L 的棒中的一维热传导问题

A_c\rho C_p \frac{\partial T}{\partial t} + \frac{\partial}{\partial x}(-A_ck\frac{\partial T}{\partial x}) = A_cQ, t \in (0,t_f), x \in (0,L)

初始条件为

T(x,0) = f(x)

两端的温度固定且已知

T(0,t) = g_1(t), \quad T(L,t) = g_2(t).

系数 A_c, \rho, C_p 和 k 分别表示横截面积、质量密度、热容及导热系数。热源以 Q 表示。

我们希望使用虚构解方法验证该问题的解。

首先，我们假设解的显式形式。考察温度分布

u(x,t) = 500 K + \frac{x}{L}(\frac{x}{L}-1)\frac{t}{\tau} K,

其中 \tau 是特征时间，在该例中为一小时。引入新的假设温度变量 u，以区分计算的温度 T。

接下来找到与假设解一致的源项。我们可以手动计算解对空间和时间的偏导，并将它们代入微分方程以得到 Q。此外，由于 COMSOL Multiphysics 支持符号处理，我们将使用该特性来代替手动计算源项。

对于材料和横截面属性均匀的情况，我们可以将 A_c, \rho, C_p 和 k 视作参数。一般异构情况和时间依赖型边界条件需要使用变量。请注意对 COMSOL Multiphysics 中的一个内置微分算子 d() 的使用，如下图所示。

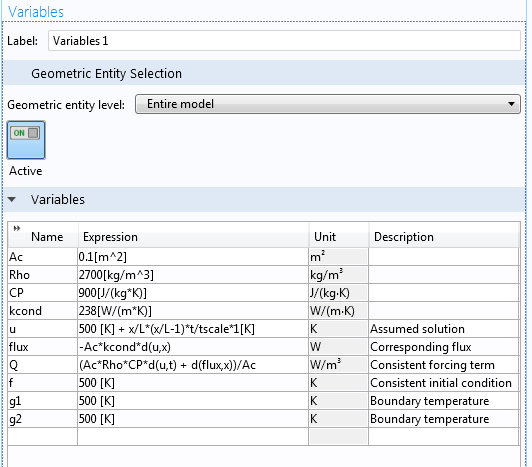
在仿真中自动计算偏导。
COMSOL Multiphysics 中的符号代数例程可自动求偏导。

我们执行符号处理的前提是选择信任符号代数。否则之后观察到的任何误差都将来自符号操作而不是数值解。当然，我们可以绘制手算的 Q 表达式图像，对比上述符号处理结果，以验证符号代数例程。

下一步，计算初始条件和边界条件。初始条件即为 t = 0 时的假设解。

f(x) = u(x,0) = 500 K。

棒两端的温度值为 g_1(t) = g_2(t) = 500 K。

下一步使用刚计算的源项及初始条件和边界条件来获取问题的数值解。在该示例中，我们将使用固体传热物理场接口。

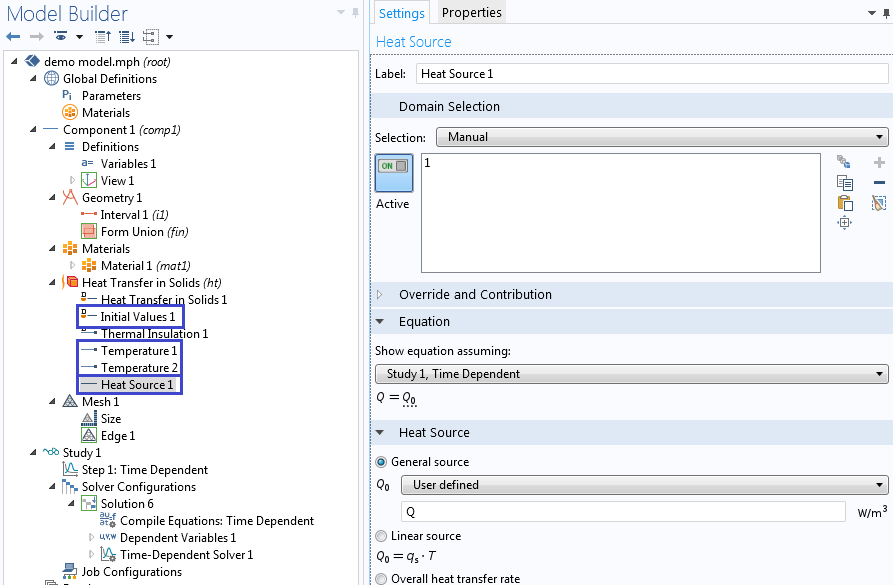
在 COMSOL Multiphysics 模型树中增加初始值、边界条件和源项。
增加初始值、边界条件以及由假设解得到的源项。

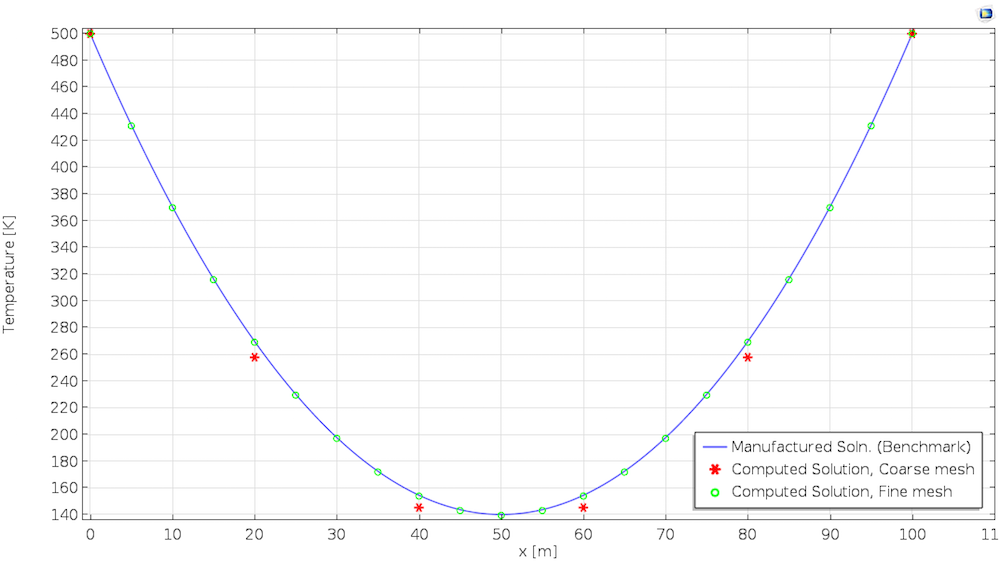
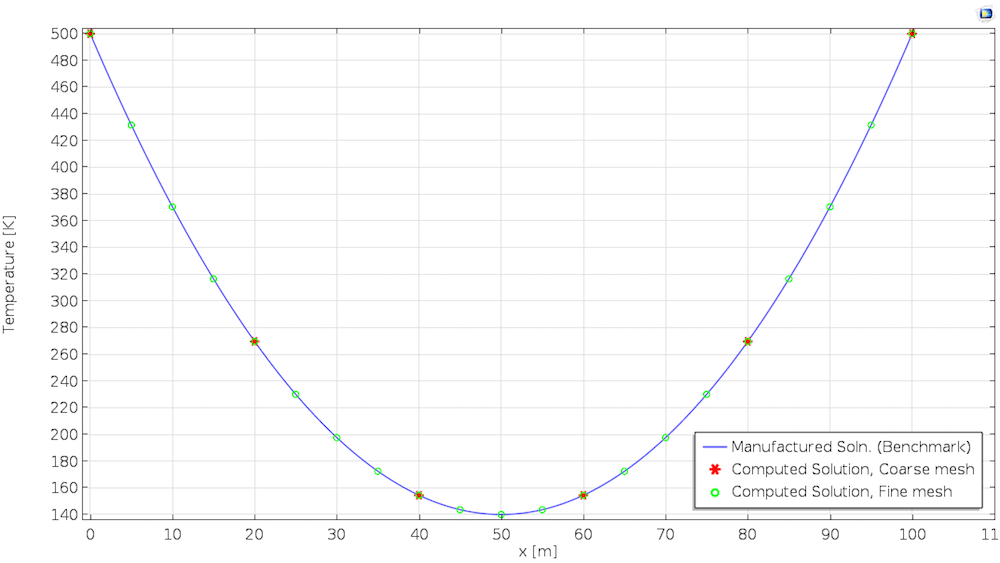
最后一步需对比数值解和假设解。下图显示了一天后的温度。第一个解使用线性单元得出，而第二个解则使用二次元得出。对于该类型的问题，COMSOL Multiphysics 默认选择二次元。

使用线性单元获得的虚构解。
使用二次元得到的解。

使用虚构解方法和线性单元计算的解（左），使用虚构解方法和二次元计算的解（右）。

检查代码的各个部分

虚构解方法使我们可以灵活地检查代码的任意部分。在上述示例中，为简单起见，我们没有检查 IBVP中的许多部分。在实际操作中，方程中的每一项都应以最常规的形式检查。例如，在检查代码是否准确表示了不均匀的横截面积时，我们需在推导源项之前 定义一个空间上可变的面积。这同样适用于其他系数，例如材料属性。

对于所有初始条件和边界条件都应进行类似检查。如果我们希望指定左端的通量而非温度，首先应计算对应于虚构解的通量，即-n\cdot(-A_ck \nabla u)，其中n是外法向单位矢量。对于该示例中的假设解，左端的向内通量变成\frac{A_ck}{L}\frac{t}{\tau}*1K。

在 COMSOL Multiphysics 中，固体传热中的缺省边界条件是热绝缘。那如何验证最左端的热绝缘？我们需要虚构一个新的解使左端没有导数。例如，我们可以使用

u(x,t) = 500 K + (\frac{x}{L})^2\frac{t}{\tau} K.

请注意，在验证时，我们需检查方程是否被正确求解。而无需考虑解是否和物理情况一致。

请记住，一旦虚构一个新的解，便需要根据假设解重新计算源项、初始条件和边界条件。当然，我们可以使用 COMSOL Multiphysics 的符号处理工具来避免上述麻烦！

收敛速率

如上图所示，由线性单元及二次元得到的解随网格尺寸减小而收敛。该定性收敛让我们对数值解有了一些信心。我们可以通过研究收敛速度来进一步检查数值方法，从而对数值程序进行定量检查。

例如，在稳态问题中，针对标准单元误差的误差估算由 m-阶 Sobolev 模 测量，且为：

||u-u_h||_m \leq C h^{p+1-m}||u||_{p+1},

其中 u 和 u_h 是实际解和有限元解，h 是最大单元尺寸，p 是近似多项式（形函数）的阶数。当 m ＝0 时，误差估计为

||e|| = ||u-u_h|| = (\int_{\Omega}(u-u_h)^2d\Omega)^{\frac{1}{2}} \leq C h^{p+1}||u||_{p+1},

其中 C 是独立于网格的常数。

回归虚构解方法，这意味着线性单元 (p= 1) 解在网格细化时应表现出二阶收敛。如果将误差模相对于网格尺寸绘制在一个对数-对数图像中，斜率应渐近至 2。否则，就需要检查代码或者输入的准确性和规则性，例如材料和几何属性。如下图所示，数值解以理论期望速度收敛。

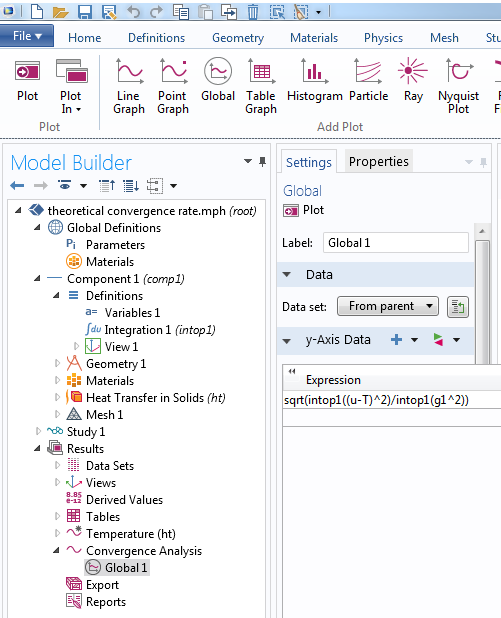
使用积分算子定义模。
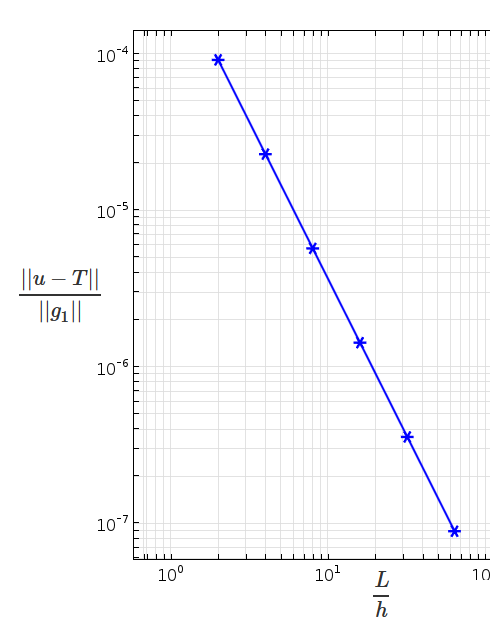
网格尺寸与误差的对数-对数对比图。

左：使用积分算子定义模。算子 intop1 被定义在域内积分。右：对数-对数误差图像和网格尺寸对比，表现了 L_2-模 (m= 0) 内线性单元的二阶收敛，和理论预期一致。

虽然我们总应检查收敛情况，但只能对上述这种存在先验误差估计的问题检查理论收敛速率。当遇到此类问题时，请记住虚构解方法可以帮助验证代码是否具有正确的渐近行为。

非线性问题和耦合问题

对于本构非线性案例，方程中的系数依赖于解。例如在热传导中，导热系数可与温度相关。对于此类情况，需从假设解导出各种系数。

耦合（多物理场）问题拥有不止一个控制方程。假定了所有场的解后，需要为每个控制方程推导出源项。

唯一性

请注意，只有控制方程组在假设解的条件（源项、边界和初始条件）下具有唯一解时，虚构解方法才有效。例如在稳态热传导问题中，需要正的导热系数来证明唯一性。对于各向同性的均匀导热系数，可以直接检查这一点，但对于温度相关的导热系数或各向异性情况，则应进一步考虑以保证虚构解不违反这类假定。

使用虚构解方法时，解通过构造而来。此外，唯一性的证明也并非仅限于存在严格解析解的情况，它的适用范围要大得多。因此，除了从源项、初始条件及边界条件来寻找精确解以外，该方法还可用于更多的情况。

自己动手操作

COMSOL Multiphysics 中内置的符号处理功能使我们可以轻松通过虚构解方法来验证代码，还可用于教学目的。虽然我们会对代码进行广泛测试，但也欢迎用户参与检查。博客介绍了一种用于验证多种物理场接口的通用工具。您也可以使用基于方程的建模或者 COMSOL Multiphysics 中的物理场开发器来验证您的操作。如果您对该技术有任何疑问，欢迎随时与我们联系！

资源

  • 有关虚构解方法及其相关优势和限制的拓展讨论，请参阅桑迪亚国家实验室的报告。该报告详细介绍了一组盲测：一位作者在另一位作者不知情的情况下植入了一系列错误代码，要求其使用本博客中介绍的方法进行扫雷。
  • 关于科学计算验证和确认的详细讨论，请参阅
    • W. J. Oberkampf and C. J. Roy, Verification and Validation in Scientific Computing, Cambridge University Press, 2010
  • 您还可在以下内容中详细了解有限元方法中的标准误差估计
    • Thomas J. R. Hughes, The Finite Element Method: Linear Static and Dynamic Finite Element Analysis, Dover Publications, 2000
    • B. Daya Reddy, Introductory Functional Analysis: With Applications to Boundary Value Problems and Finite Elements, Springer-Verlag, 1997

博客分类

相关主题

评论 (0)

正在加载...
浏览 COMSOL 博客
类别
标记