
投石机是一种大型攻城武器,在中世纪或奇幻电影中经常可以看到它的身影。这种武器依靠将势能转化为动能来远距离投掷物体。投石器看似简单,实则有着一套复杂的动力系统。在这篇博客中,我们将使用“多体动力学模块”构建一个简化的配重式投石机模型,并重点研究一些设计特征。
战狼:终极攻城武器
投石机是一种远程武器,它使用杆的摆动向目标投掷重物。战争一方通常利用它破坏城墙。有时也会用它投掷希腊火药(Greek fire),造成更大规模的混乱和伤亡。观众可以在一些电影和电视节目中看到投石机的身影,比如《魔戒:王者归来》(2003);《马可波罗》(2014–2016);甚至在较早的《巨蟒与圣杯》(1975)中,城堡守卫竟然向着城外毫无戒心的亚瑟王砸了一头牛!
历史上,曾有一架名为战狼 的著名投石机,当时的英国士兵称之为“Ludgar”。1304 年,在一次征讨苏格兰的战役中,英格兰国王爱德华一世在围攻斯特林城堡之前命令手下的工程师建造一架巨型的投石机,那就是有史以来最大的投石机——战狼。传言它能在 200 多米开外投掷出 150 公斤左右的巨石。

战狼的小型复制品,这个配重式投石机在摆动臂的末端安装了巨岩投石索。图片由 Ron L. Toms提供。在 CC BY 3.0 授权下使用,通过维基共享资源分享。
这种大型投石机的配重质量一般相当于抛射物的十倍,也就是说,战狼的配重约为 1.5 吨!只要战狼发动了攻击,对方的士兵基本很难幸存,面对强敌,驻守在城堡内的苏格兰军队不得不投降。但当时爱德华一世急于尝试新建造的投石机,拒绝接受投降。他强迫苏格兰人留在城堡里,重新发动了围攻。战狼再次证明了自身的价值,其他事情,都交由历史去评价。
投石机的工作原理很简单。配重抬起,投石机撬高;当投石机发射时,配重降下,系统的势能转换成动能与势能之和。抛射物经历摆动后沿轨迹在特定点释放,释放点发生在投石索一端从摆动臂顶端滑离时。
对配重式投石机进行多体分析
在此例中,我们用“多体动力学模块”和COMSOL Multiphysics® 软件 5.3 版本构建了一个简易的投石机计算模型。
模型采用了下列假设和外形尺寸:
- 假定所有部件为刚性(包括投石索)
- 假定所有铰接关节不产生摩擦
- 使用罚刚度防止抛射物穿入地面
- 垂直杆长度为 L5 = 3.5 m,固定在地面上,代表支架
- 配重质量(M = 2000 kg)与抛射物质量(m)的比值为 100
- 配重悬挂在长度为 L4 = 1 m 的竖杆上
- 摆动臂总长 6 m,其中 L1 = 1 m
- 投石索长度为 L3 = 3 m
配重式投石机的模型示意图。
当抛射物被摆动臂投掷到另一边时,这个过程是非平凡的变速运动。如果投石机设计追求的是最远投掷距离,这就产生了一个问题:在发射轨道的哪一点上发射重物,才能使投掷距离最远?基础力学指出,如果忽略空气阻力和抛射物在发射时距离地面的高度,抛射物的投掷距离 s(测量标准为 x 轴正方向)可以表示为
其中 v0 和 α 分别表示抛射物在发射时的速度和角度,g 表示重力加速度。
因此,寻求最远的投掷距离,相当于寻找使 s 值最大化的 v0 和 α 组合。你可能下意识地认为发射角度应该是 α = 45°。我们看一看该值是否适用于投石机模型。
下方动画演示了投石机的运动。动画绘制了投射轨迹上的 s 值,即在弹道的某一点上发射抛射物后的投掷距离。
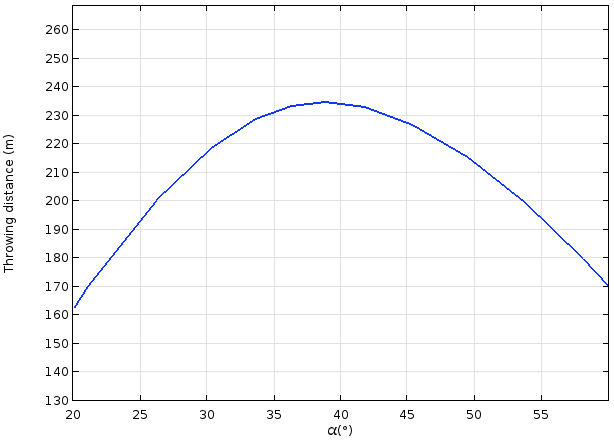
从下方投掷距离与发射角 α 函数关系绘图中可以看出,当在 α ≈ 38° 的位置上发射物体,此时的抛射距离达到最远。结果表明,投掷角度与最佳角度的偏差小于 5° 时,只会对投掷距离产生数米的影响。换句话说,只要发射角度大致无误,投石机就能发挥预期效果。
现在我们来研究一下,如果在参数扫描中把投石索拉长或缩短 10%,将会产生什么影响?如下图显示,投石索的最大长度对最远投掷距离影响巨大。所以,如果你在为中世纪的国王设计投石机时,应该特别注意这个设计参数。
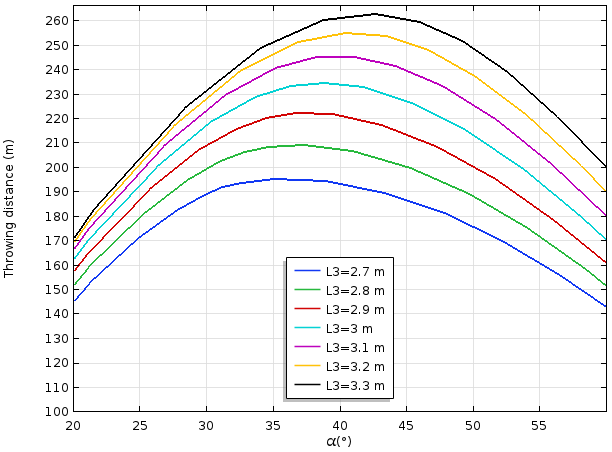
借助参数化扫描,你能够轻松查看模型中其他的物理长度变化所带来的影响(与此同时,配重应保持固定高度,使仿真一致)。欢迎访问“案例下载”库来获取模型文件,并亲手操作模型。
结束语
在本篇博客中,我们演示了如何利用“多体动力学模块”建立一个简单的配重式投石机模型。如果你有兴趣了解更多关于多体动力学建模的信息,请阅读下列博客文章:
知道为什么战狼又被称作 Ludgar 吗?显然,英国士兵读起战狼的法文名称——Loup de Guerre——时总是磕磕巴巴,因而将它缩写成“Ludgar”。



评论 (0)