
超材料是一种人工材料,其性能取决于特定的结构设计而非化学成分。此类材料的结构往往很复杂,因此制造难度相当大。在文本中,我们将通过数值研究探讨一种能够在静水压力的作用下膨胀的多孔弹性超材料(由带空隙的单一材料制成)。
超材料与 3D 打印结合
“3D 打印”和“超材料”是“COMSOL 博客”版块的两个热门话题。它们具有广阔的应用前景,能够制造定制的医疗植入物,打印房屋,应用于声学隐形技术,是改变我们周围世界的前沿科技潮流。

3D 打印机。图片由 Jonathan Juursema 提供。在 CC BY-SA 3.0 许可下使用,通过 Wikimedia Commons 分享。
通过两种技术的结合,我们可以使用直接激光写入(direct-laser-writing,简称 DLW)打印来制造复杂的超材料,这种工艺对于其他制造技术而言相当困难或不可能实现。这个想法的灵感来源于德国卡尔斯鲁厄理工学院(Karlsruhe Institute of Technology)和法国勃艮第弗朗什-孔泰大学(Université de Bourgogne Franche-Comté)的研究小组。他们共同研究了在稳定和静态条件下表现出独特的负等效压缩性力学性能的超材料。
研究具有负等效压缩效应的多孔弹性超材料
研究人员的多孔弹性超材料是一种人造三维复合材料,当周围环境产生的静水压力增加时,将发生各向同性的膨胀。大多数天然弹性材料的反应与之相反,当周围的静水压力增加时,它们的体积会变小。

海绵是一种受多孔弹性现象影响的材料。
那么为什么超材料会膨胀呢?为了回答这个问题,让我们来观察一下超材料。超材料由单一的普通固体成分构成,材料内为中空的三维十字结构,此结构内部的隐藏空间包含恒压空气。每个十字的末端都有圆形的膜片。
当周围压力与十字结构中的压力不同时,膜片向内或向外弯曲。在膜片变形的作用下,与膜片非对称相连的杆状物使十字结构旋转。如果外部的静水压力大于内部的压力,那么单个旋转就会转化为结构的各向同性膨胀,导致负的等效压缩性。
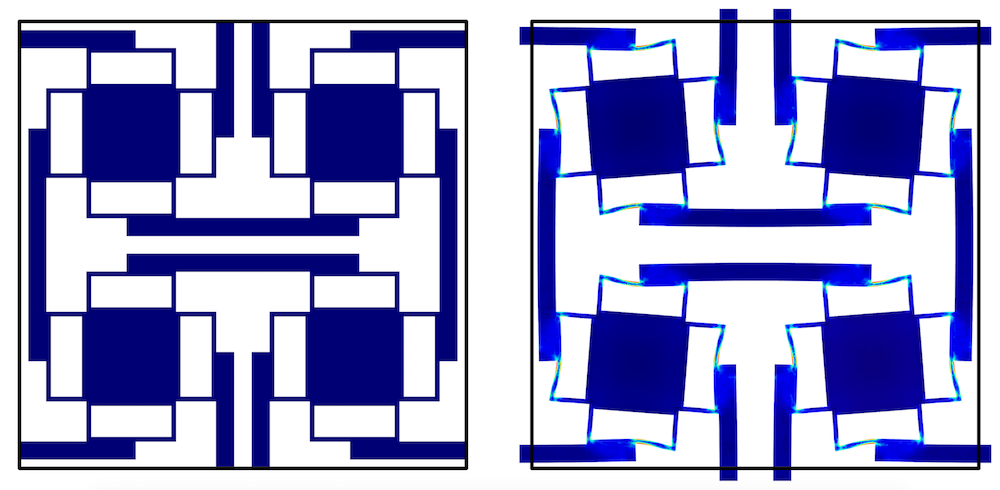
零压力下(左)和压力增大后(右)的晶胞,图片描述了负压缩性的原理。图片来自 Jingyuan Qu 和 Muamer Kadic 。
这种负压缩性看似违反了物理定律,但等效的体积增加与材料内看不到的体积减少是相对应的。这样可以保证结构稳定。
使用 COMSOL Multiphysics® 分析新颖的多孔弹性超材料
为了研究新颖的多孔弹性超材料的结构细节,研究人员选择使用 COMSOL Multiphysics® 软件。当被问及数值建模方法的优势时,研究小组的成员 Jingyuan Qu 提到了求解方程的便利性。
超材料模型是一个单晶胞。为了观察当材料内外存在压力差时所发生什么情况,他们在模型的所有外表面上施加了压力增量作为法向力。此外,该模型是在周期性边界条件下进行模拟的,这使得研究人员能够成功地找到等效的材料参数。
请注意,“结构力学”和“MEMS 模块”内置了可用的周期性边界条件。
在研究中,小组进行了两项主要的数值实验:
- 末端为自然边界条件(自由)的有限尺寸研究(一个晶胞)
- 使用了周期性条件(假设)的无限扩展的情况
在实验中,研究小组使用标准的线弹性方程:
0 = \nabla\cdot \sigma + \mathbf{F}_V \\
\sigma = \mathbf{C}\colon\epsilon \\
\epsilon = {\frac{1}{2}}[{(\nabla\mathbf{u})}^{T}+(\nabla\mathbf{u})]
\end{array}
现在,让我们研究一下第二个数值实验。
利用周期边界条件
当模拟无限材料时,我们需要应用周期性条件,使晶胞的每一个边都以各向同性的方式收缩或膨胀。首先,创建并根据方向 x+、x-、y+、y-、z+ 及 z– 来命名结构的每一侧。然后创建探针变量,用于计算“减号”侧(dispx,dispy,dispz)的平均位移,如下方第二张截图所示。
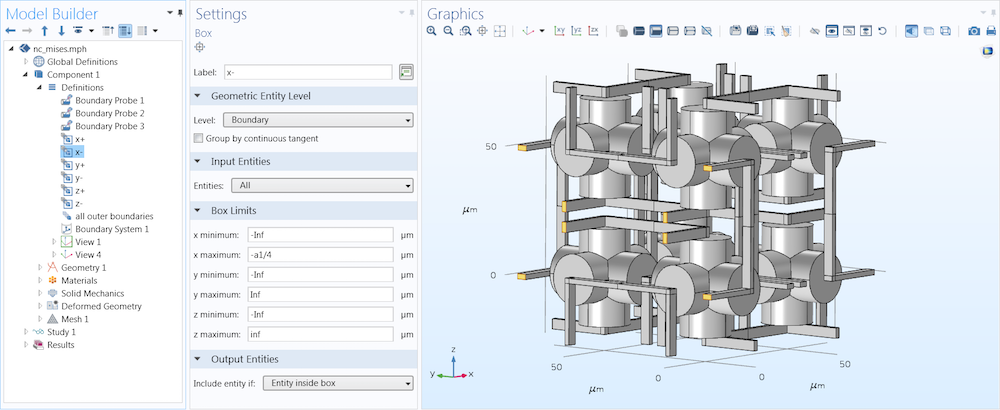
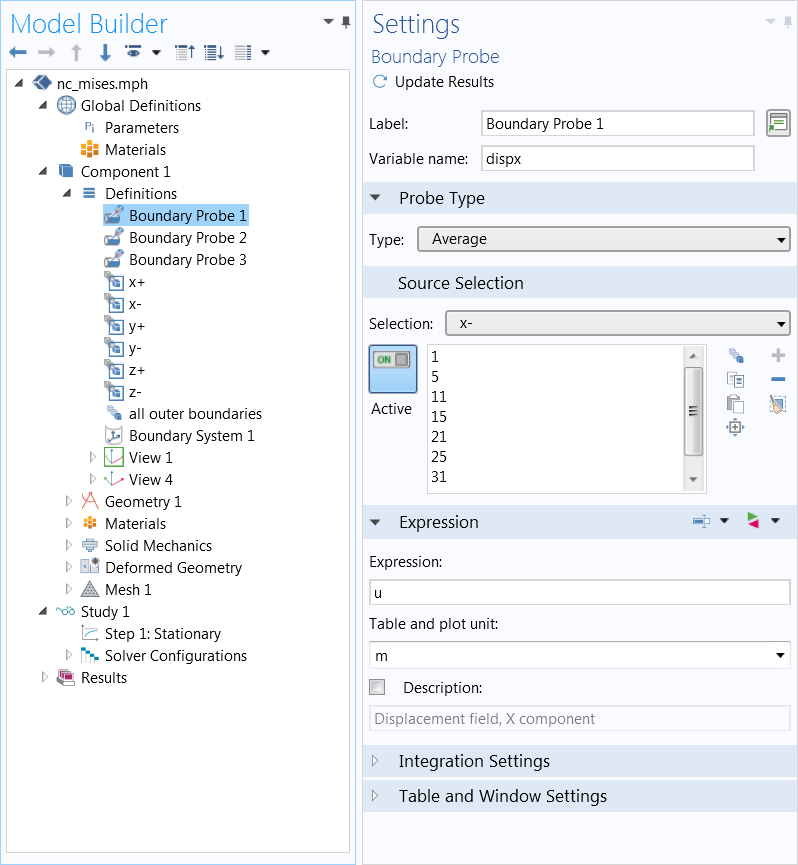
以 x 方向为例,图片显示如何选择与下一个晶胞相连的边界,展示了六个平面(上图)之一和边界探针设置(下图)。图片来自 Jingyuan Qu 和 Muamer Kadic。
下一步,将探针变量用作两边的边界条件(指定位移)。也就是,在 x– 边界上,x 方向的位移被设为 dispx,在 x+ 边界上则设为 -dispx。然后针对其他周期性切边设置类似的边界条件。因为位移 dispx 是未知数,所以使其成为解的一部分。由于指定位移的成对反作用力必须为零,所以结构会膨胀或收缩,使合力为零。
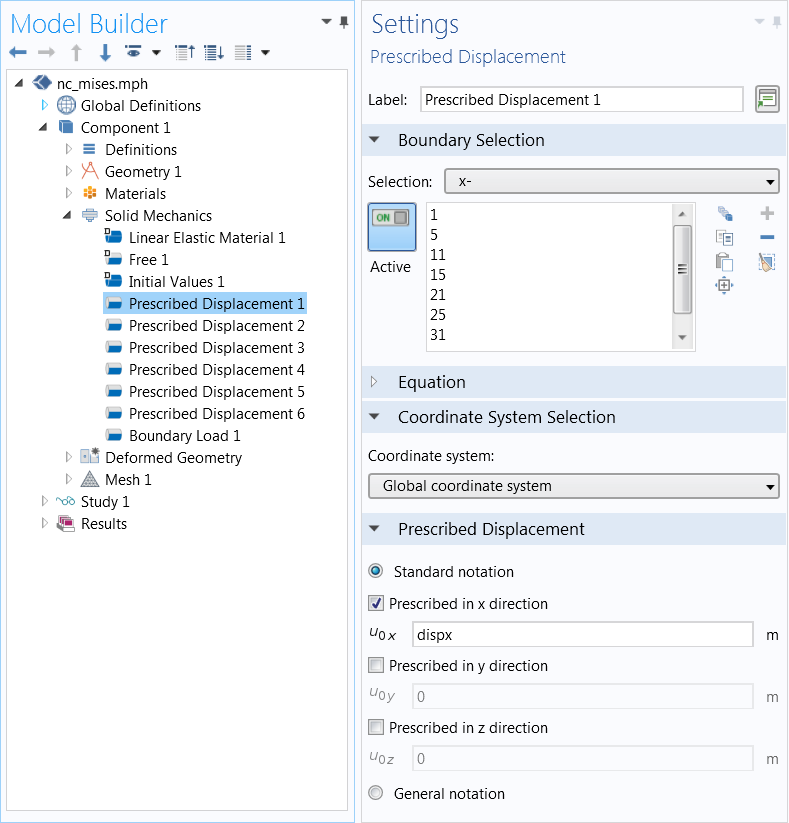
指定探测位移。图片来自 Jingyuan Qu 和 Muamer Kadic。
下一步,施加外部压力。选定几何的外部边界,并采用很大的角度公差后,模型显示未选定隐藏体积的内部边界,如下图所示
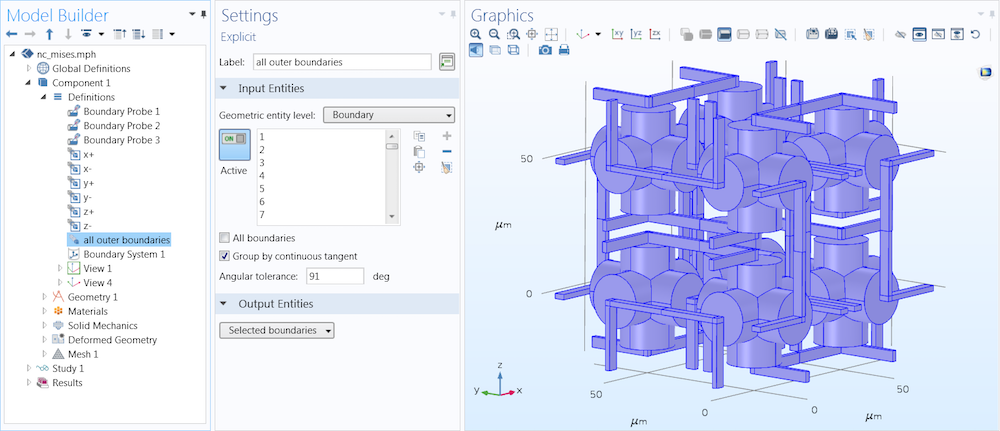
外部边界设置。图片来自 Jingyuan Qu 和 Muamer Kadic。
然后施加静水载荷作为边界荷载,即压力(P)。
S\cdot\mathbf{n}= {\mathbf{F}}_{A} \\
{\mathbf{F}}_{A}=-P\mathbf{n}
\end{array}
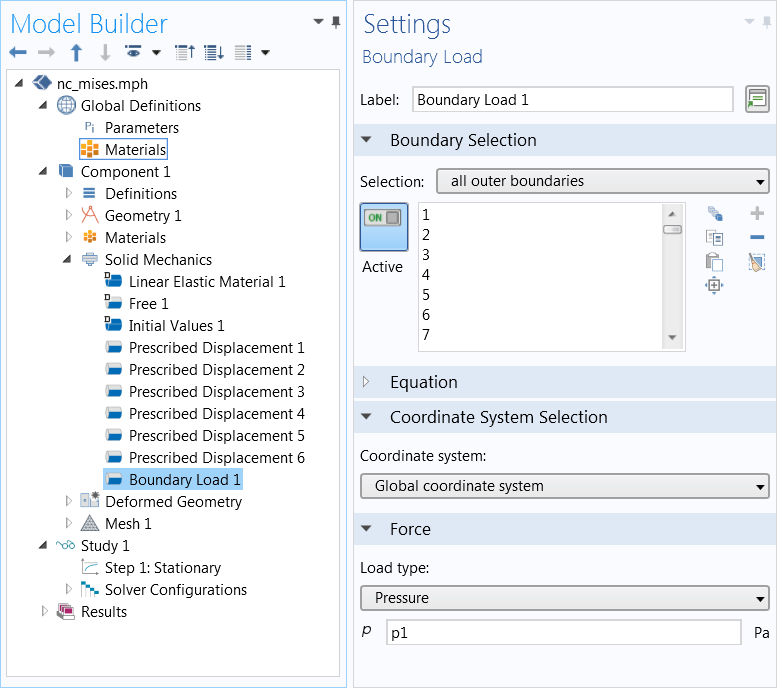
添加作用于所有外边界的法向力作为静水压力。图片来自 Jingyuan Qu 和Muamer Kadic。

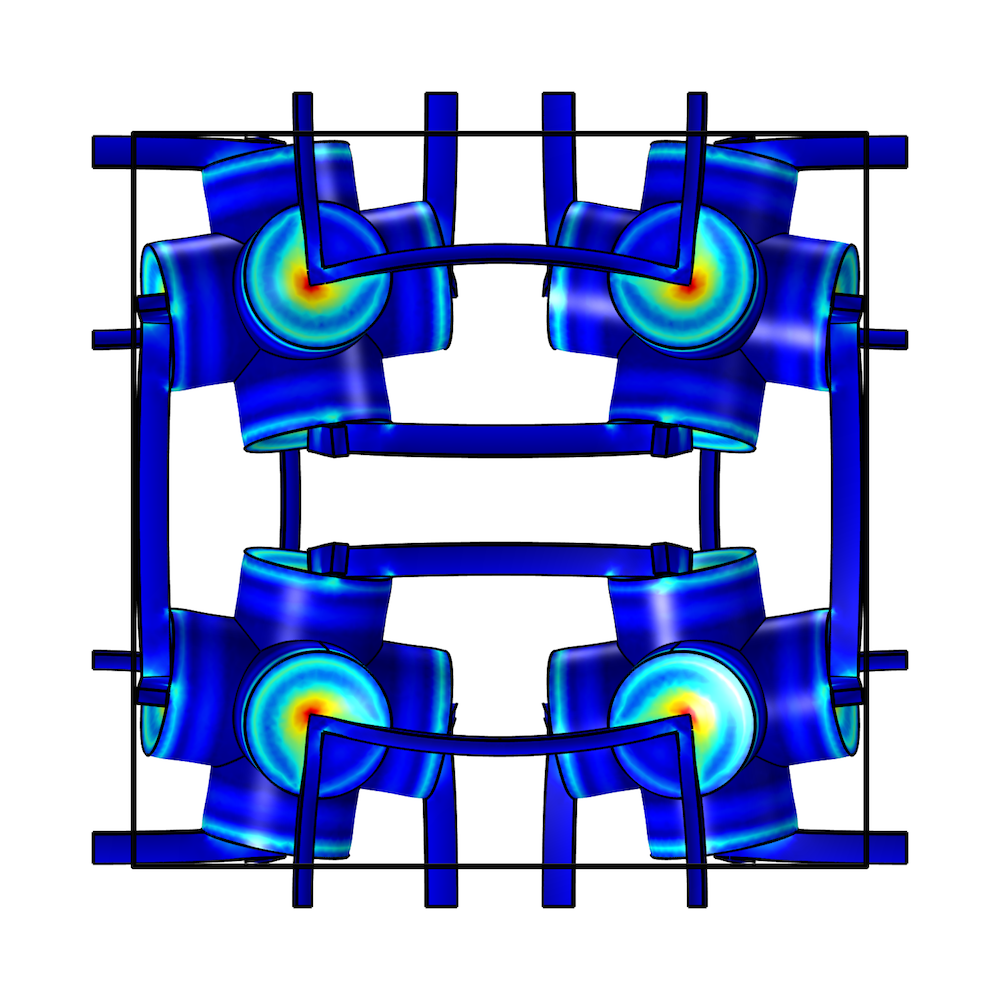
多孔弹性超材料结构的多角度视图。图片来自 Jingyuan Qu。
作为比对点,研究人员还研究了一个普通的多孔结构和一个由连续各向同性材料制成的立方体。当周围的静水压力增大时,两个结构的体积都会缩小。在相同的条件下,多孔超材料则会膨胀,突出了自身的等效压缩性特征。
后续步骤
通过大量的研究,该小组能够捕获超材料的行为,改进设计,并利用这些信息加快进入制造阶段。虽然利用传统的加工技术来制造这类材料并非不可能,但是 3D 打印可以作为制造负压缩性超材料的替代选择。3D 打印机可以使用在静水压力下收缩的普通材料来制成这种超材料。
Qu 指出,因为即使在高压环境中,超材料也能够保持恒定不变的等效体积,或许可以在高压应用中发挥特殊作用。
了解更多关于超材料的信息
- 查看研究人员的原创论文:
- 阅读这些与超材料相关的博客文章:





评论 (3)
磊 赵
2021-11-04您好,请问这个案例的教学案例有吗?谢谢
Haoze Wang
2021-11-09 COMSOL 员工您好,目前没有和多孔弹性超材料相关的案例,建议您根据博客中的内容建立模型,如有问题可发送support@comsol.com获得技术支持。
佳 刘
2023-07-20i appreciate you for the sharing. it’s very helpful for me !!