由 Ed Fontes 创作的所有博客
2024 年欧洲杯官方比赛用球的空气动力学仿真
探索 2024 年欧洲杯官方比赛用球的复杂设计，了解它与 2018 年FIFA世界杯® 比赛用球的不同。
在 COMSOL Multiphysics® 中模拟点蚀
当全面腐蚀过程持续进行时，金属表面可能会出现凹坑，这也被称为 Evans drop 实验。
模拟跑车侧门和后视镜上的风载荷
在这篇博文中，我们使用大涡模拟 (LES) 和结构分析来分析高速行驶的跑车的门和侧视镜上的风载荷和气流。
在 COMSOL Multiphysics® 中模拟快速检测
想知道 COVID-19 的快速检测测试究竟是如何工作的？ 在此处获取全面说明，以及 COMSOL Multiphysics® 中的 3 个示例模型。 （第 2 部分，共 2 部分）
快速检测测试设备中的物理原理
基于侧流分析 (LFA) 的快速检测测试，也称为免疫色谱测试，可以被认为是非常先进但非常强大的微型实验室。 （第 1 部分，共 2 部分）
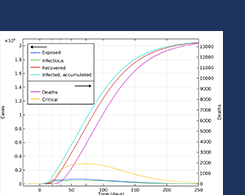
使用 COMSOL Multiphysics® 模拟 COVID-19 的传播
从易感者，暴露者，感染者到恢复者：了解数值模型如何帮助我们了解COVID-19大流行的动态及其传播方式。
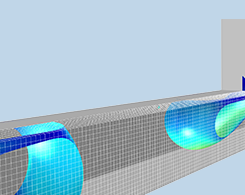
COMSOL®中的多相流建模与仿真：第 1 部分
多相流通常包括气-液、液-液、液-固、气-固、气-液-液、气-液-固或气-液-液-固混合物的流动。此系列博客主要讨论气-液和液-液混合物，并简要讨论固-气和固-液混合物。此外，我们还将介绍 COMSOL 软件中 CFD 模块和微流体模块中的模型和模拟策略。 不同尺度的多相流建模 通过数学建模可以对不同尺度的多相流进行研究。最小尺度约几分之一微米，而最大尺度可达几米或几十米。这些尺度甚至可以相差大约八个数量级，其中最大尺度可能比最小尺度大一亿倍,这意味着，在整个尺度范围内，使用同一种机理模型在数值上是无法解析从最小尺度到最大尺度的多相流。因此，多相流模拟通常分为不同的尺度。 在较小的尺度上，可以详细模拟相边界的形状；例如，气泡与液体之间的气液界面的形状。在 COMSOL 软件中，这种模型称为分离型多相流模型，而描述此类模型的方法通常被称为表面追踪法。 在较大的尺度上，如果必须详细描相界面，该模型方程将无法求解。相反，此时会采用场（如体积分数）来描述不同相，同时将表面张力、浮力和相间质量传递这类界面效应作为分散多相流模型方程中的源和汇。 分离型多相流模型详细描述了相边界，而分散型多相流模型仅考虑分散在连续相中的一个相的体积分数。 上图显示了分离型和分散型多相流模型的主要区别。上述两种示例，均使用函数 Φ 来描述气相和液相。但是，在分离型多相流模型中，不同相之间相互排斥并存在一个清晰的相边界。在此边界上，相场函数 Φ 发生突变。除了追踪相边界的位置以外，相场函数没有任何物理意义。 在分散型多相流模型中，函数 Φ 描述了气相（分散相）和液相（连续相）的局部平均体积分数。通过平均体积分数可以在该区域的任一点顺利找到介于 0 和 1 之间的值，这预示着在其他均质域中是否存在少量还是大量气泡。也就是说，在分散型多相流模型中，可以在同一时间和空间点上定义气相和液相；而在分离多相流模型中，在给定的时间和空间点上，只能定义气相或液相。 分离型多相流模型 对于分离型多相流的模拟，COMSOL Multiphysics® 软件提供了 3 种不同的界面追踪方法： 水平集法 相场法 动网格法 水平集和相场都是基于场的方法，其中相界面代表水平集或相场函数的等值面。动网格法与上述两种方法完全不同，它将相界面模拟为分隔两个域的几何表面，其中每个域对应不同的相。 基于场的问题通常是在固定的网格上求解，而使用移动的网格可以解决动网格问题。 下图的动画显示了一个 T 型微通道中生产乳液的模拟结果，该模型使用相场法求解。在动画中，我们可以看到相边界与网格的平面和边缘不一致，相边界由相场函数的等值面表示。 在相场法和水平集法中，有限元网格不必与两个相的边界一致。 与之相反，下图显示了含动网格的上升气泡的验证模型。网格与相边界的形状保持一致，并且网格边缘与相边界重合。但是，动网格模型也有缺点，即气泡的变形使两个次级气泡从母气泡分离。此时，必须将原始相边界划分为几个边界。该方法太复杂，并且尚未在 COMSOL® 软件中实现。因此，COMSOL® 软件中的动网格法无法处理拓扑变化。而相场法不存在这个缺点，它可以处理相边界形状的任何变化。 上升气泡的验证。当两个次级气泡脱离母气泡时，发生了拓扑变化。 什么时候使用相场法和动网格法？ 对于给定的网格，动网格法具有更高的精度。基于这一优势，我们可以直接在相边界上施加力和通量。为了解析该表面的等值面，基于相场的方法需要围绕相边界表面建立密集网格。由于很难定义一个精确贴合等值面的自适应网格，通常必须在等值面周围建立大量密集网格。在具有相同精度的情况下，相较于动网格，这样做会降低基于场的方法的表现。那么，什么时候使用这些不同的方法呢？ 对于不希望发生拓扑变化的微流体系统，通常首选动网格法； 如果需要拓扑变化，则必须使用相场法： 当表面张力的影响较大时，首选相场法 如果可以忽略表面张力，首选水平集法 分离型多相流模型和湍流模型 在湍流模型中，由于仅解析平均速度和压力，流体的细节会丢失。从这一点来看，表面张力效应在流体的宏观描述中也变得不那么重要。由于湍流表面的流动也比较剧烈，几乎不可能避免拓扑变化。所以对于湍流模型和分离型多相流模型的组合，最好使用水平集法。水平集法和相场法都可以与 COMSOL Multiphysics 中的所有湍流模型结合使用，如下图和动画所示。 在COMSOL Multiphysics中，所有湍流模型都可以与相场法和水平集法相结合来模拟两相流。 将水平集法与 k-e 湍流模型相结合来模拟反应堆中水和空气的两相流。 分散型多相流模型 在相边界过于复杂而无法解析的情况下，必须使用分散型多相流模型。 CFD 模块提供了 4 种（在原理上）不同的模型： 气泡流模型 适合高密度相中包含较小体积分数低密度相的情况 混合模型 适合连续相中包含较小体积分数的分散相（或几个分散相），其密度与一个或多个分散相相近的情况 欧拉–欧拉模型 适用于任何类型的多相流的情况 可以处理任何类型的多相流，且气体中有密集颗粒，例如流化床 欧拉–拉格朗日模型 适合包含相对较少（成千上万，而不是数十亿）的气泡、液滴或悬浮颗粒流体 适合气泡、颗粒、液滴或使用方程模拟的颗粒，该方程假定流体中每个颗粒的力平衡 什么时候使用不同的分散型多相流模型？ […]
数字孪生模型和基于模型的电池设计
通过将高保真多物理场模型与轻量级模型以及实测数据相结合，工程师可以创建数字孪生模型，进而去理解、预测、优化并控制现实界系统。