
对于物理学家来说,随时都可能迸发出更好的设计和技术灵感。对于一个饥饿的物理学家来说,灵感尤其会在用餐时迸发出来。例如,一个经验丰富的厨师可以轻松地想出一种烹饪可丽饼(法式煎饼)的方法,但对于一个家庭厨师来说,可能会产生挫败感。在研究怎样烹饪这道经典美食的过程中,两名研究人员通过仿真来探讨是否可以制作出完美的煎饼……
煎饼制作和最佳覆盖问题
法式煎饼不仅种类多样而且美味。薄薄的可丽饼可以包裹甜的或咸的食材,像烟熏三文鱼、草莓和奶油等,它的基本成分是你的厨房里可能已经有的常用原料:面粉、鸡蛋、牛奶、糖、黄油和盐。这些配料看起来很简单,煎饼的实际制作却非常困难。这是一道需要精心制作的美食,不仅要轻薄、松软,最重要的是,还要摊平且没有结块,这样做出的煎饼才美味可口。但这说起来容易做起来难,我们很多人都可以证明这一点!
那么,制作煎饼的最佳方法是什么?为了制作出厚度均匀、形状完美的煎饼,我们需要一些专用设备(还没有用到仿真软件……),包括:
- 搅拌器
- 冰箱
- 涂抹用具
- 锅铲(如果需要的话,用于翻转)
- 不粘锅
在制作面糊时,需要将配料搅拌或混合均匀,直到稠度稀薄、几乎呈流动状,当然不能有结块。如果想要制作甜的煎饼,可以添加一些糖或少许香草。如果想要制作咸的,可以添加一些草本植物。然后,将面糊放在桌子上静置 30 分钟,或者放入冰箱中冷藏过夜更好,这一点非常重要。这一步将确保煎饼面糊有时间消除掉混合过程中产生的所有气泡。静置完成后,可以将面糊舀到加热好的平底锅中开始制作。面糊在锅里如何扩散很重要,两位流体动力学家决定深入研究最佳覆盖问题(和平底锅)的根源。
煎饼的最佳覆盖意味着最终成品是薄厚均匀、无孔且完美的圆形。但是,由于面糊一沾到锅就开始煎制,而且面糊会不断扩散,要均匀地覆盖比想象中要难的多!许多厨师都知道要倾斜平底锅并搅拌面糊,或者使用涂抹工具将面糊摊得更均匀,使其尽可能平整地贴在平底锅表面。尽管许多人都知道如何凭直觉掌握这个技术,但这个项目背后的物理学家却想知道这些技术是否可以改进,以及他们是否可以通过数值仿真来优化煎饼的制作过程。

左图:煎饼面糊在锅中没有均匀摊开,无法达到最佳覆盖效果。右图:有结块的煎饼。
巴黎综合理工学院(École Polytechnique)的流体动力学专家兼助理教授爱德华·布乔说:“这项研究的动机实际上来源于厨房。” 故事是这样的:一个星期天,坎特伯雷大学(University of Canterbury)机械工程学教授马修·塞利尔在自己家厨房里做煎饼。他对煎饼不完美的形状感到沮丧,塞利尔称其为“顽固的小麻烦”,他认为应该有更好的制作方法。终于,他的妻子受够了他的抱怨,提醒他说:“你是个流体动力学家,你应该能为此做些什么!”
听了妻子的话,塞利尔决定接受这个挑战,他开始寻求制作完美煎饼的方法。塞利尔与他在 2016 年蒙特利尔举行的一次会议上认识的物理学家布乔一起合作,使用 COMSOL Multiphysics® 软件进行研究,将自己的专业优势发挥到了极致。塞利尔是自由表面和薄膜方面的专家,而布乔是最优控制方面的专家。
使用 COMSOL Multiphysics® 模拟平底锅中的面糊流动和硬化
在建立流体动力学模型中,当涉及基板运动和液体层之间的相互作用时,通常需要依靠离心力来驱动流体的运动,而基板运动则需要围绕垂直轴(角速度可变)旋转。
但是,煎饼的制作过程在这方面有所不同。面糊的运动不是由离心力而是由重力驱动的,而且锅得运动也不是单一旋转,而是绕多个轴的瞬态旋转。到目前为止,还没有人对这种流体流动进行模拟,研究人员认为这是研究液层固化及其应用领域的一个机会。
Boujo 说: “最初这只是一个业余项目,但很快我们发现它适用于任何需要厚度均匀的液体薄膜的情况。” 他解释说,这对于许多需要非常薄且均匀的涂层的工业过程至关重要,例如智能手机显示屏,太阳能电池,电子电路板等。
建立模型需要采用已发表文献中的方程和策略,并针对这一特定的流体动力学和最优控制问题进行修改。为了获得面糊和平底锅的运动,研究人员采用了基于梯度的优化方法,该方法通常用于解决许多优化变量的问题。这种方法与灵敏度分析相结合,可以确定数千个优化变量的灵敏度,而计算成本与正向问题的相近。
研究人员之所以选择 COMSOL Multiphysics 对这个问题进行模拟和优化,是因为他们希望确保数值方法能够保持流体的总质量守恒,而 COMSOL® 软件中的偏微分方程(PDE)求解器可以轻松实现这一点。Boujo 说:“COMSOL 使用方便、灵活,我们能够很轻松地实现伴随方程。” 此外,LiveLink™ for MATLAB® 为他们进行优化提供了一种便捷方式。Boujo说: “用 MATLAB ® 编写的主要代码负责处理下降算法,并在需要时调用 COMSOL® 来求解直接方程或伴随方程。”
研究团队还需要根据薄膜厚度的演变、传热和基板运动的影响等方面来考虑问题的多物理场特性。首先,他们模拟了流体在静止基底上和时谐运动的基地上的扩散行为。即:
其中, A_1,A_2,T_1,和 T_2 是将要使用蒙特卡罗方法优化的参数,用于提高薄膜的均匀性。
优化问题被设置为一个最小化问题,因为薄膜的均匀性是通过测量平面轮廓的平方偏差 {\cal U}(t_f)获得的,
(t_f) = \int\int \left(h(x,y,t_f)-h_\mathrm
{opt}\right)^2dxdy,
其中, h(x,y,t) 是面糊轮廓,h_\mathrm{opt} 是面糊采用圆柱坐标时的轮廓高度。
然后,通过允许运动参数 \theta(t) 和 \beta(t) 为任意值,他们对问题进行了更深入的研究,但这也极大地增加了优化变量的数量,从而需要将基于梯度的优化和伴随灵敏度分析相结合。此外,通过在目标函数上添加一个惩罚项 \cal C,来避免极端运动 {\cal J}_t。使用常数 \gamma 缩放该惩罚项,用于控制极限运动。
评估流体动力学仿真的结果
研究结果表明,基于梯度的优化策略优于蒙特卡洛方法。如下图所示,目标函数(左)和均匀性的平方偏差(右)是避免极端运动的参数 \gamma 的函数。左图显示,更极端的运动可以得到更平坦的煎饼,而基于梯度的优化(实心圆)明显优于蒙特卡洛方法。当惩罚项较大时,蒙特卡洛方法会带来更好的均匀性,但目标函数更差(见左图)。这正说明了蒙特卡洛方法的随机性,而不具有任何技术优势。
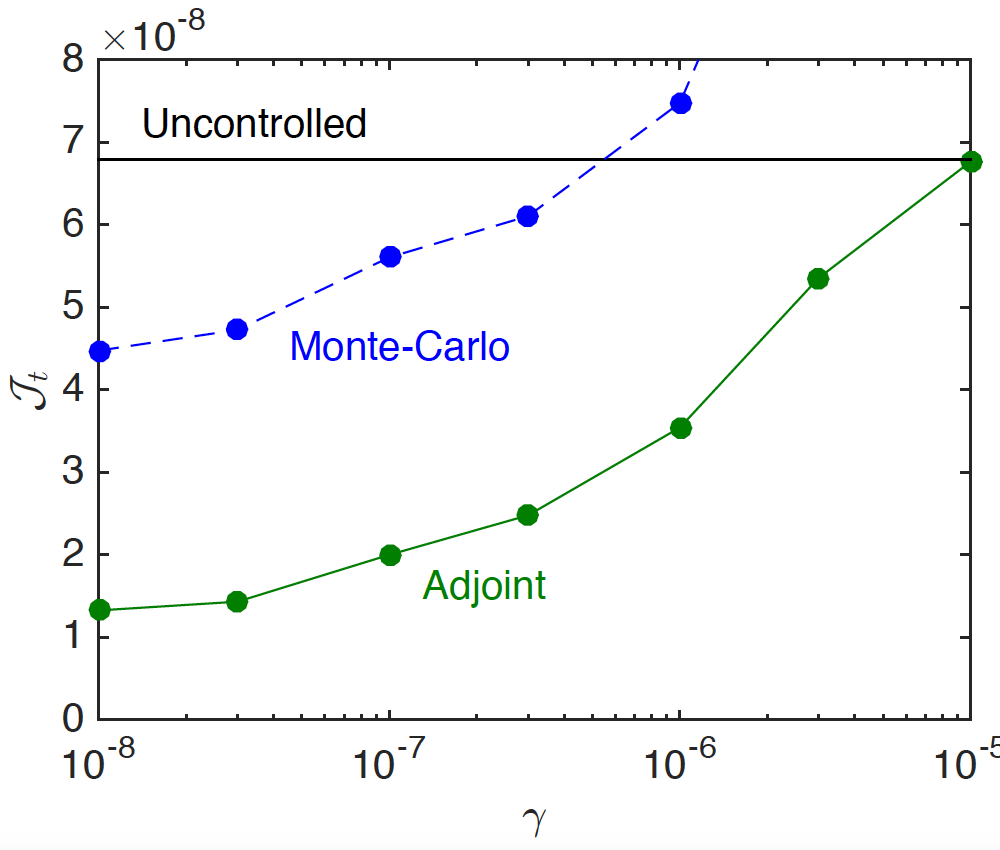
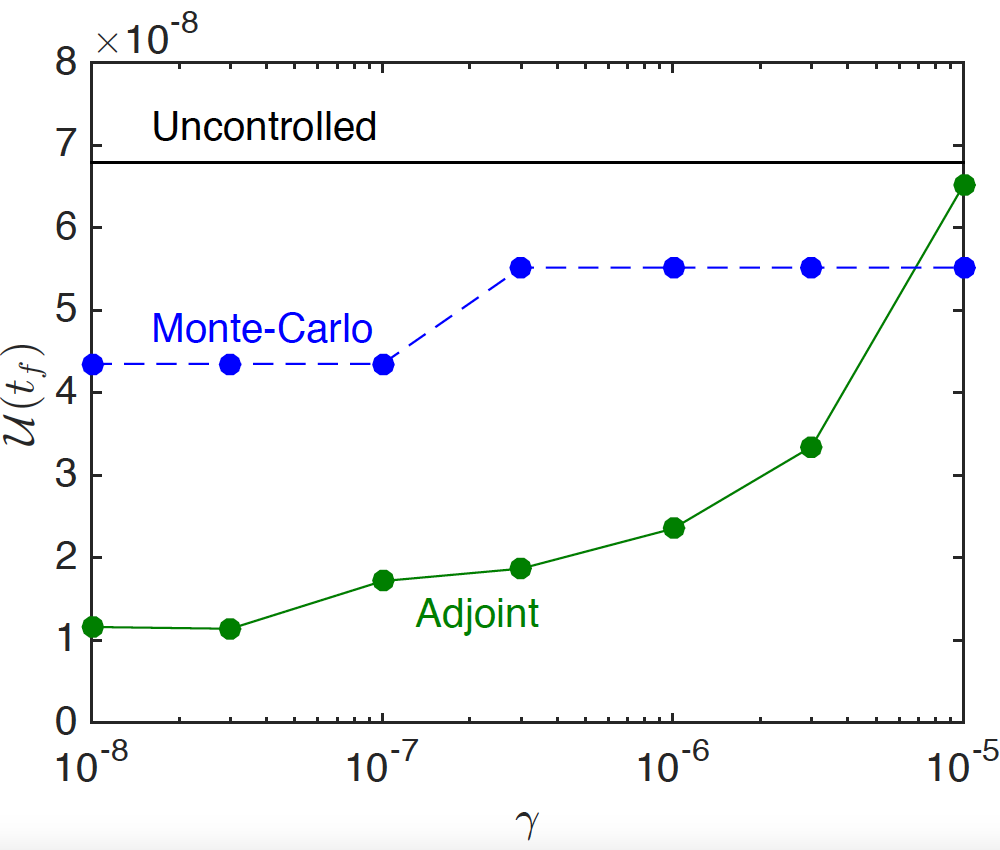
左图:目标函数 {\cal J}_t 与惩罚参数 \gamma的关系 。右图:最终的均匀性 { U}(t_f) 与惩罚参数的关系。图片由 Boujo 和 Sellier 提供。
在找到最佳的时谐运动(左下图)之后,研究人员进一步通过伴随优化方法找到最佳控制率对这些结果进行了优化,帮助他们获得最佳的薄膜厚度等值线(右下图)。
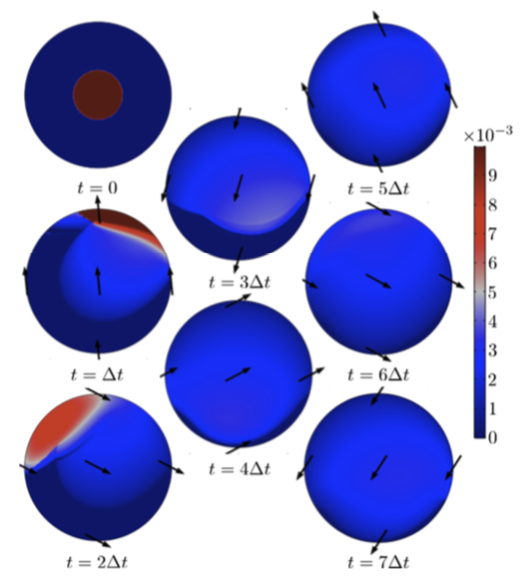
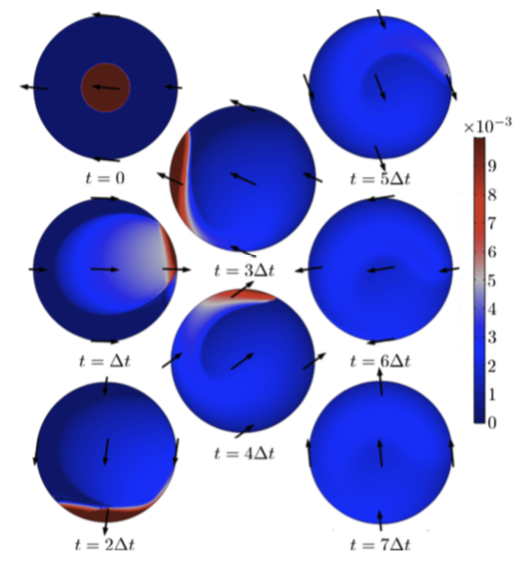
左图:采用蒙特卡罗方法获得的时谐波运动学最小 {\cal U}(t_f) 时的薄膜厚度等值线 h(x,y,t)。右图:采用最佳任意控制 \gamma = 10^{-8} 时的薄膜厚度 h(x,y,t)等值线。这两幅图中的箭头都显示了重力在平面表面上的投影方向。图片由 Boujo 和 Sellier 提供。
至于最终的结果,我们可以比较瞬态运动学与最优谐波运动学和最优任意运动学在两个惩罚参数\gamma下的结果。对于每一种情况,最终的膜都会变得越来越均匀和平滑。另外,基于梯度的优化方法比蒙特卡洛方法的计算成本更低。
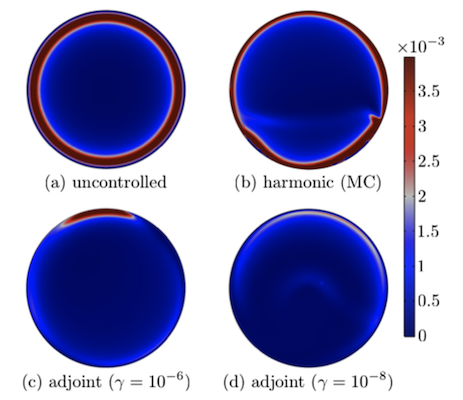
无控制(a)、最优谐波控制(b)、次优任意控制(c)和最优任意控制(d)情况下,最终的薄膜厚度梯度平方。图片由 Boujo 和 Sellier 提供。
制作煎饼的最佳方法是什么?都在手腕上
那么如何使用 Boujo 和 Sellier 的研究结果来制作出更好的煎饼?当面糊一碰到锅时,你就应该倾斜平底锅,以使所有面糊都流向锅边。然后,将平地锅旋转一到两次,使面糊覆盖其余锅底表面,并逐渐减小倾斜角度。然后,再将平底锅放在火炉上,很快你就可以说 “ voilà-早午餐做好了!”

尽管我的翻面技术可能还需要一些练习(出现了裂缝),但面糊在平底锅中的分布更均匀了(左),而且成品也更好(右)。
进一步的思考
Boujo 和 Sellier 发现他们从研究结果中得出的最佳平底锅晃动动作与厨师们在做的动作非常相似。他们说: “至少在制作煎饼这件事中,能够确认人们是最好的“直觉优化者”,这真是太好了。”
此外,他们很快就发现,他们方法的好处已经超越了烹饪领域。Boujo 说: “我们正在努力向更复杂的实际应用迈进。”通过对这种类型的流动进行模拟,他们发现,除了手机显示器和太阳能电池所需的薄膜外,在某些情况下, “移动基板可能是例如旋转涂层,叶片涂层和蒸汽沉积等工业过程中目前采用的其他技术的良好替代方案”。
无论你是一直在努力完善煎饼制作技术的家庭厨师,还是对这类流体流动问题感兴趣的工程师,这两位流体动力学专家似乎都能帮到您。
下一步
- 在 Phys.org 上阅读相关文章:“通过流体动力学完善制作可丽饼的技术”
- 阅读 COMSOL 博客,了解有关流体-结构相互作用的更多信息:模拟多体机构中的流体-结构相互作用
MATLAB 是 The MathWorks,Inc. 的注册商标。





评论 (0)