如何在 COMSOL Multiphysics^® 中生成随机表面

为了轻松生成随机几何表面，COMSOL Multiphysics^® 软件提供了一组功能强大的内置函数和算子，例如均匀和高斯随机分布函数以及非常有用的 求和 算子。这篇博客，我们将介绍如何使用一个几乎“线性”的表达式生成一个随机表面，并对决定表面粗糙度性质的空间频率分量进行详细控制。

表征表面粗糙度

表征粗糙表面的方法有很多。一种方法是使用它的近似分形维数，即表面分形维数在 2~3 之间。分形维数值为 2 的表面是一个普通的、近乎绝对光滑的表面; 分形维数值为 2.5 表示一个相当崎岖的表面; 分形维数接近 3 表示一个“3D 空间填充”。相应地，分形维数为 1 的曲线几乎处处光滑，1.5 表示一条相当崎岖的线，接近 2 表示近似“2D 空间填充”。

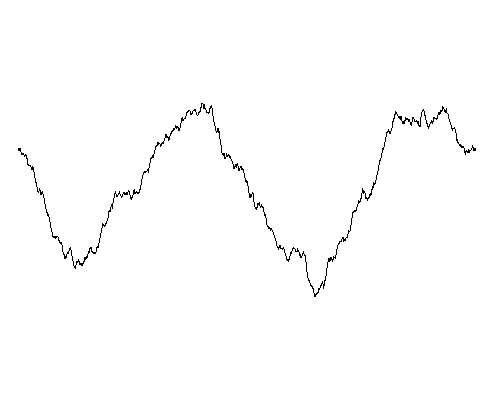
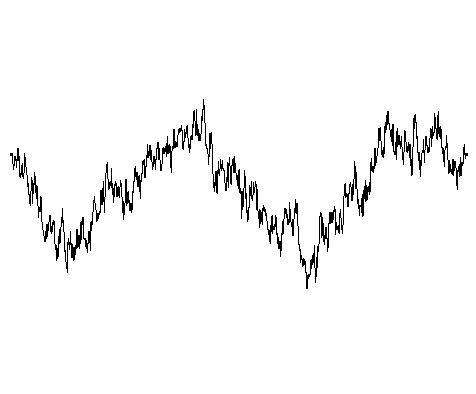
曲线的分形维数的范围从 1 (左)到大约 1.2 (中)，再到 1.6 (右)。

使用分形维数度量是一种有用的近似方法，但需要记住，真实的表面在超过几个数量级的尺度上不是分形的。真实表面具有空间频率“截止”点，因为它们的尺寸有限，而且当其被“放大”后，我们会发现一些新的微观结构特征。

空间频率组成是表征表面粗糙度的另一种方法。这可以被转换成一种合成表面数据的构造方法，通过使用类似于傅里叶级数扩展的三角函数之和来实现。总和中的每个项都表示通过空间振荡的某个频率。这也是本文将使用的方法。在介绍一系列三角函数之前，我们先快速复习一下空间频率和元波的概念。

空间频率

在物理学中，随时间变化的振荡频率使用类似于下列数学表达式的形式表示

其中，频率 f 的单位是 1/s，也称为赫兹或 Hz。

通过空间的振荡具有相应的空间频率，如下面的表达式所示，只需将时间变量 t 替换为空间变量 x，将时间频率 f 替换为空间频率 v 即可。

式中，空间频率的 SI 单位为 1/m。

空间频率通常由波数 k= 2πv 表示。

一个相关的量是波长 \lambda=\frac{1}{\nu}，它与频率和波数有关，如下式所示：

空间可能有多个维度，因此可能存在多个空间频率。在 2D 中，使用笛卡尔坐标表示：

式中，\bf{k}=(k_x,k_y)=(2\pi \nu_x,2\pi\nu_y) 为波矢量，并且\bf{x}=(x,y)。

波矢量 \bf{k} 表示波的方向。

元波

一个粗糙的表面 f（x，y）可以看作是由许多以下列形式的元波组成

式中，φ 是相位角。

由于，sin(\theta)=cos(\pi/2-\theta)，相位角也可以用正弦函数表示。

对于完全随机的表面，应该认为相位角 φ 可以取任何值，例如，0 到 π 或 –π/2 到 π/2
之间。当为一个随机表面合成元波时，可以在长度为 π 的区间内均匀随机分布中挑选 φ，因为表达式 cos(\phi) 可以取 -1 到 +1 之间的所有可能值。请注意，如果选择的间隔大于 π ，则可能会出现终点或环绕效应。这是由于根据 cos(\pi\theta)=-cos(\theta)，余弦函数镜像对称，步长为 π。

为了获得可用于仿真的有效表述，我们只允许一组离散的空间频率：

ν_x = m， ν_y = n

式中，m 和 n 是整数。

考虑一个由以下形式的元波组成的表面：

通过使 m 和 n 取正值和负值的概率相等，我们应该能获得一种能合成一个没有预选振荡方向的表面。

请注意，如果采用这种方法，每个波方向将被表示两次。例如，方向(-2,-3)与(2,3)相同;(2,-1)与(-2,1)相同；等等。

如果空间频率 m 和 n 可以分别取最大整数值 M 和 N，将对应于一个高频截止：

由于也可以取负值，因此存在负截止值：

在 x 方向上具有空间频率截止 \nu_{xmax}=M 意味着可以表示的最短波长是 \lambda_{xmin}=\frac{1} {M}，对于y方向也是如此，即 \lambda_{ymin}=\frac{1}{N}。

元波的相关振幅

每个元波都有一个相关的振幅，因此每个组成波分量具有以下形式：

最终表面为这些波分量的总和：

最简单的振幅选择是从一个均匀分布或高斯分布中选择系数 A_mn。但是，事实证明，这不会生成看起来特别自然的表面。在自然界中，在如磨损和侵蚀这样的不同的过程中，慢速振荡比快速振荡更有可能具有更大的振幅。在离散情况下，这对应于逐渐减小的振幅，根据某种分布：

式中，谱指数 β 表示较高频率衰减的速度。根据 分形图像科学（参考文献1），谱指数与表面的分形维数相关，但仅适用于覆盖任意高频的无限系列波，并且仅适用于指数的某些范围。在实践中，合成表面的振幅 a(m，n) 将使用有限数量的频率乘以具有高斯分布的随机函数 g(m，n) 生成：

a(m,n) = g(m,n)h(m,n)

选择高斯分布或正态分布来获得一个平滑但随机变化的振幅，并且幅度没有限制。

相位角 φ 将从函数 u 中采样，函数 u 在 –π/2 和 π/2 之间具有均匀随机分布：

φ(m,n) = u(m,n)

总结

为了表示粗糙表面，我们希望使用下式的二重求和：

式中，x 和 y 是空间坐标;m 和 n 是空间频率;a（m，n）是振幅; φ（m，n）是相位角。该表达式类似于截断的傅里叶级数。尽管该级数是用余弦函数表示的，但由于角度求和的规则，相位角使得该求和可以表示一个非常通用的三角级数：

确定周期性

根据函数 f*(x，y) 的定义， 它将是周期性的。为了获得自然的表面，应该通过让 x 和 y 在某些有限值之间变化来“切出”适当的一小部分;否则，合成数据的周期性就会很明显。这些值应该是什么？

整体周期性将由最慢的振荡决定，分别对应于 x 方向和 y 方向的空间频率 m= 1 或 n= 1。这使每个方向上的周期长度为 1。

我们可以在矩形 [a, a + 1] × [b, b + 1] 或更小的矩形上生成表面，来“避免”周期性。

在 COMSOL Multiphysics^® 中定义参数和随机函数

关于如何在 COMSOL Multiphysics 中实现，首先根据下图定义几个空间频率分辨率和谱指数参数：

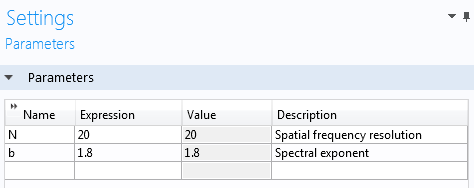
生成振幅需要在两个变量中有一个高斯分布的随机函数。COMSOL 软件的 全局定义 节点提供了这个功能：

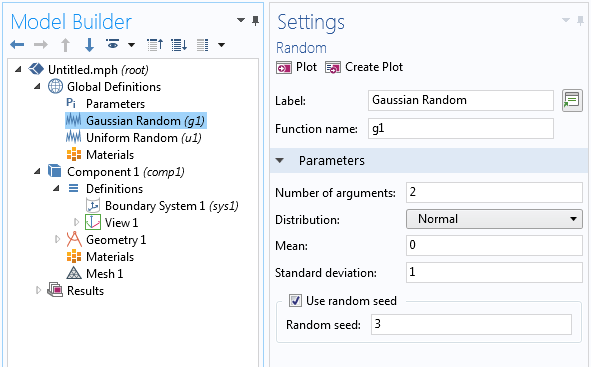
在这里，标签 和函数名称 已分别更改为高斯随机 和 g1。此外，变元数 被设置为 2 而不是默认值 1，分布类型设置为 正态，对应于正态分布或高斯分布。

对于相位角，采用类似的方式，需要在 –π/2 和 π/2 区间内有一个均匀的随机函数：

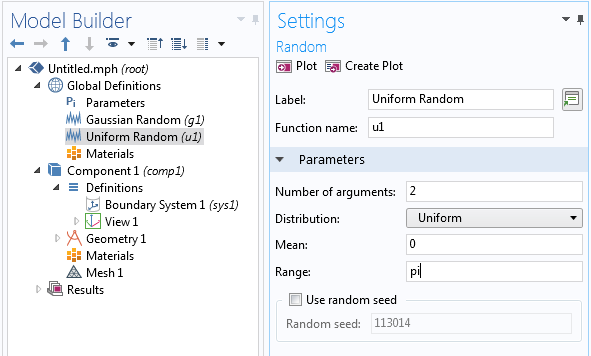
标签 更改为 均匀随机，函数名称 更改为 u1，变元数 更改为 2，范围 更改为 pi。

可以选择使用随机种子，以在每次使用相同的输入参数时获得相同的表面。

定义参数化曲面

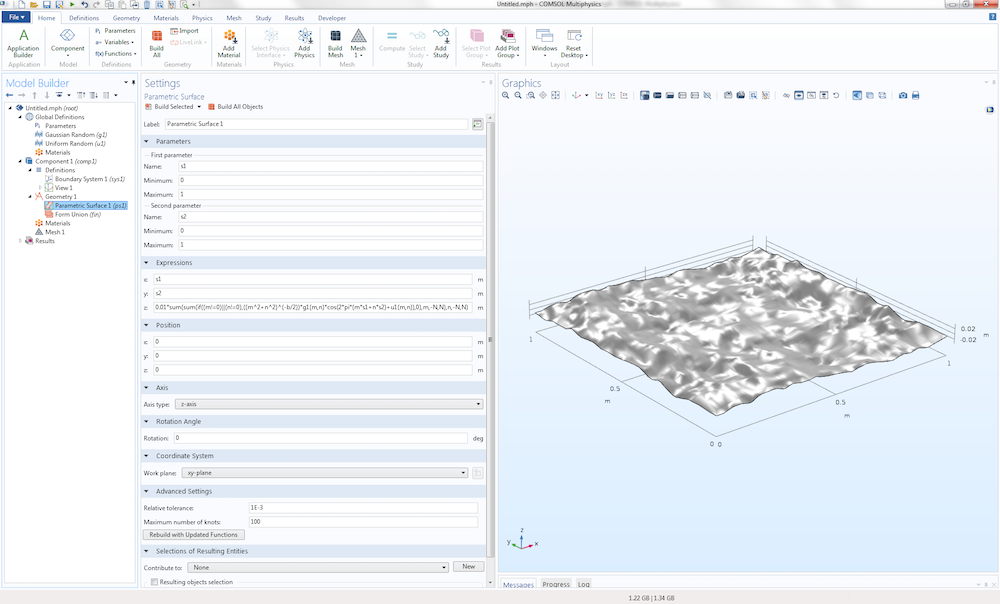
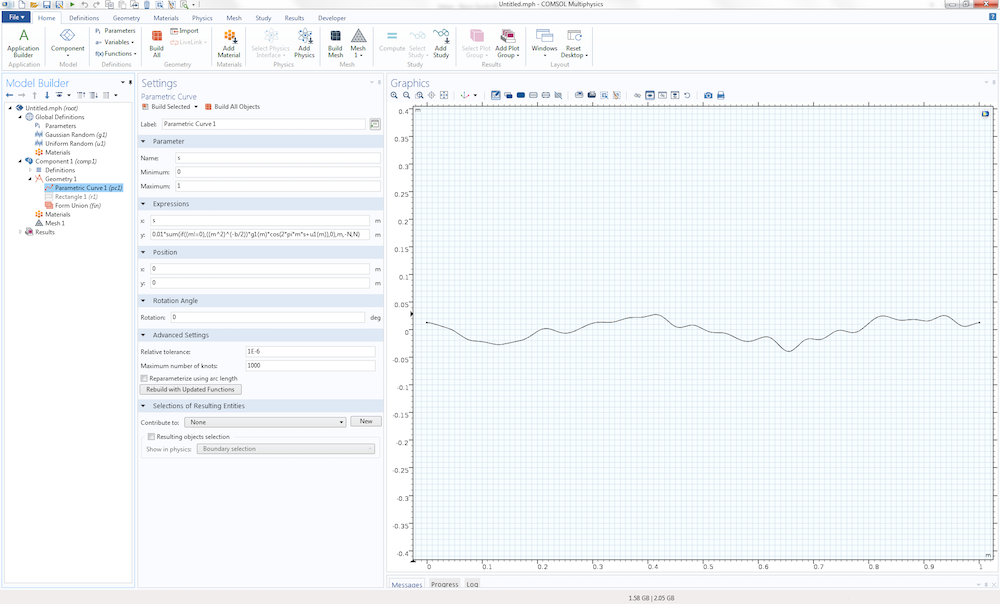
接下来，几何 下添加一个 参数化曲面 节点，使用一个相当长的 z 坐标表达式，如下所示：

0.01*sum(sum(if((m!=0)||(n!=0),((m^2+n^2)^(-b/2))g1(m,n)*cos(2*pi(m*s1+n*s2)+u1(m,n)),0),m,-N,N),n,-N,N)

其中，x=s1 和 y=s2 在 0 和 1 之间变化。

系数 0.01 用于在 z 方向上缩放数据。或者，该比例因子可以被应用到振幅系数中。

参数化曲面几何特征用于生成一个合成的随机表面。

请注意，每当更新参数化曲面的任何参数或表达式时，都需要单击设置窗口的 高级设置 部分中的 使用更新的函数重建 按钮。

这个表达式是整数参数 m 和 n 在 –N 到 N 之间的二重求和。如果将其与前面的数学讨论进行比较，可以看到已经设置了 M=N，并产生了一个方形补丁表面。m 和 n 同时为零的项对应于不需要的“DC”项，并通过 if 语句从总和中消除。

sum() 算子的语法如下：

sum(expr,index,lower,upper)

对于所有从 低 到 高 的索引，它计算了通用表达式 expr 的总和。

if() 算子的语法如下：

if(cond,expr1,expr2)

条件表达式 cond 的计算结果为 expr1 或 expr2，具体取决于条件的值。

在这个示例中，通过将 最大结数 设置为 100（默认值为 20），提高了参数化曲面的分辨率。此外，相对容差 被放宽到了 1e-3（默认值为 1e-6）。参数化曲面的底层表示基于非均匀有理 B 样条曲线 （NURBS）。更多的结点对应于表示更精细的 NURBS 分辨率。因为我们并不过分关注本例中生成表面的近似精度，所以放宽了容差。

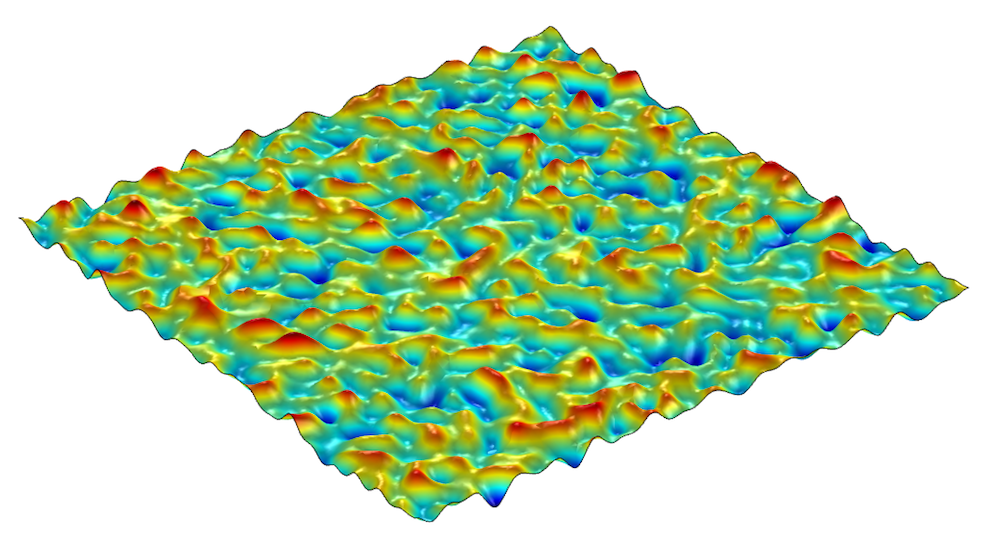
通过生成网格，可以获得有用的表面可视化图，如下所示。

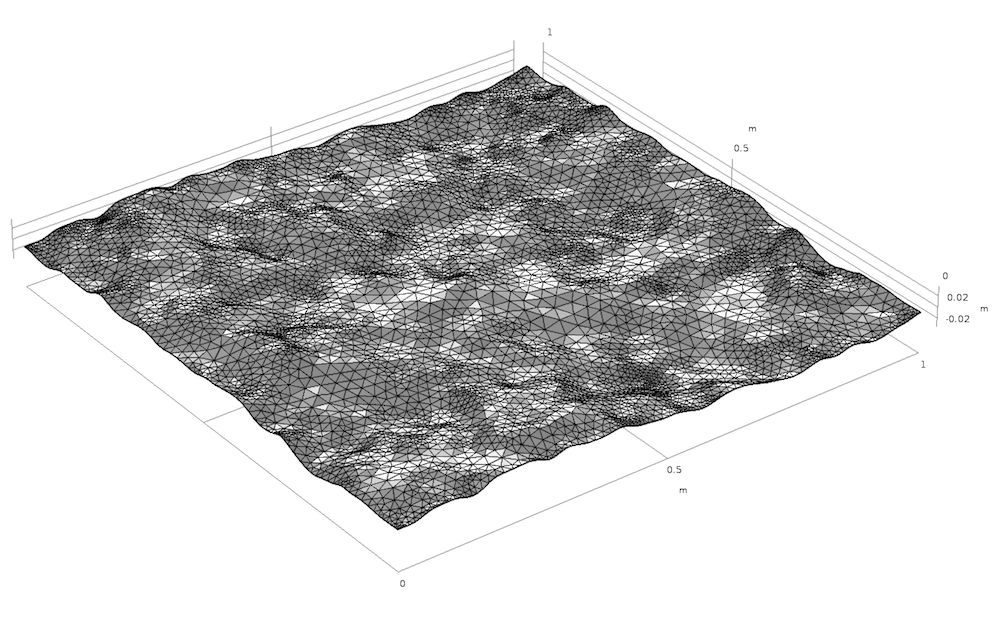
一个划分了网格的随机表面。

请注意，N = 20 意味着假设使用 SI 单位，最快的振荡为 1/20 = 0.05 m。x 和 y 方向的周期性可以分别在 x= 0，x= 1 和 y= 0，y= 1 的平行于 y 轴和 x 轴的曲线处看到。

为了更清楚地看到周期性，我们可以在正方形 [0,2] × [0,2] 上绘制表面：

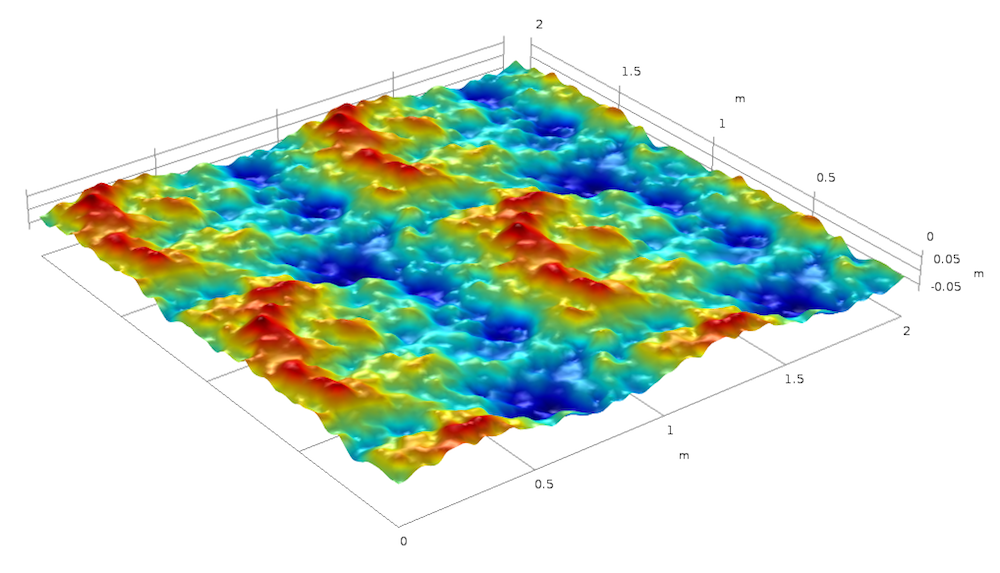
正方形 [0，2] × [0，2] 上的表面周期性。表面高度用彩色表示。

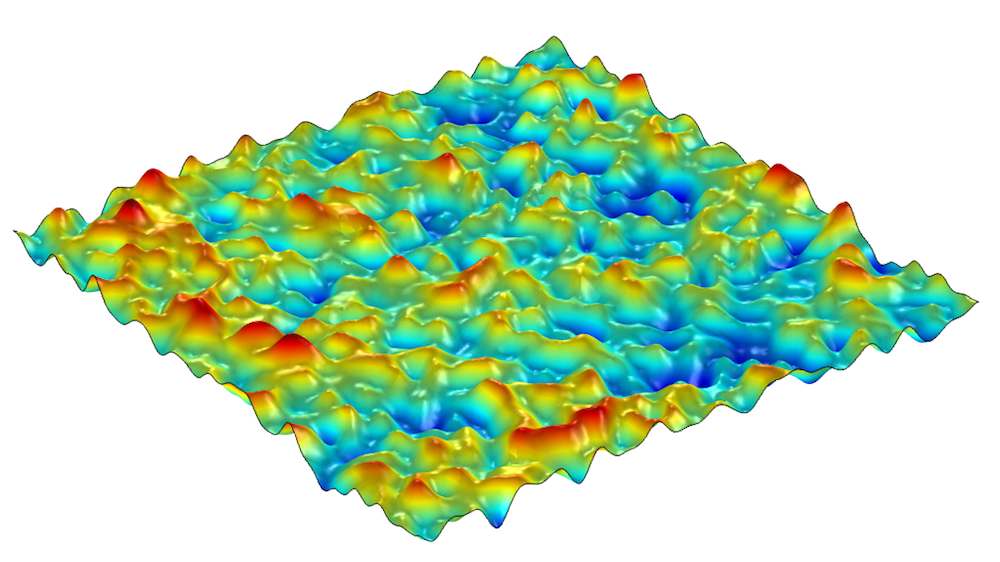
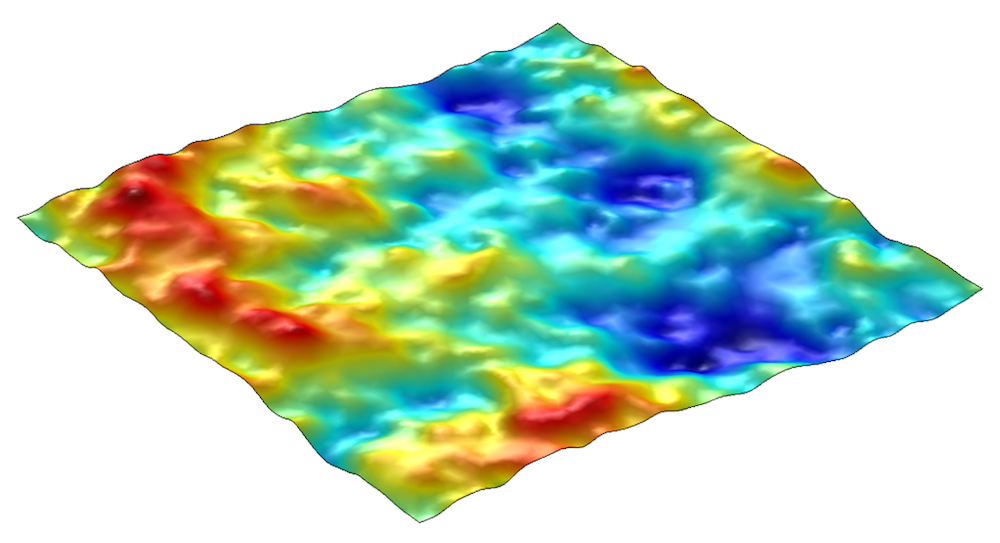
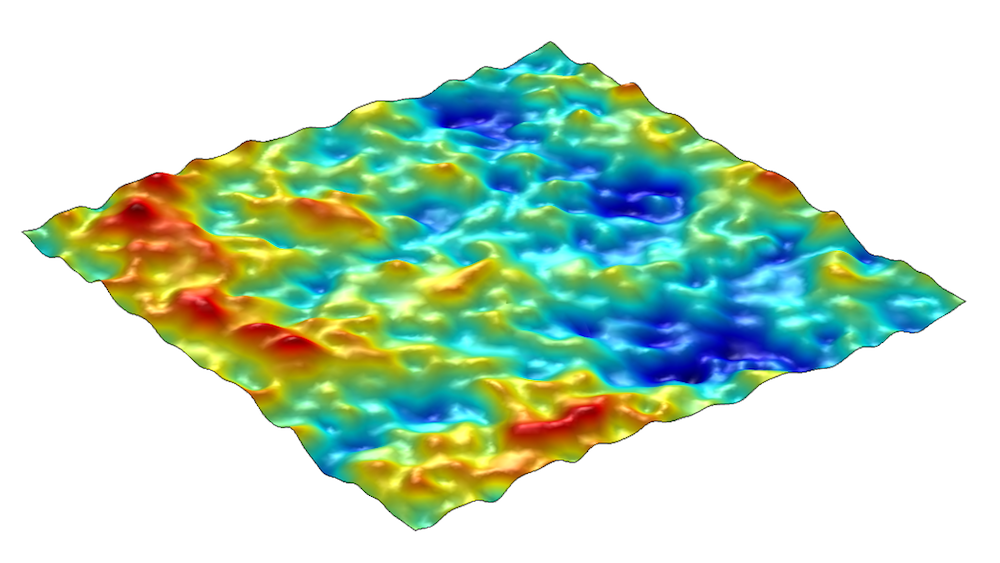
在正方形 [0，1] × [0，1] 上生成的表面，方法是从左上角图像顺时针方向叠加 20 个频率分量，振幅谱指数 β = 0.5、β = 1.0、β = 1.5 和 β = 1.8。表面高度用彩色表示。

在分析中使用表面数据

在 COMSOL Multiphysics 中，这种类型的随机生成表面可用于任何类型的物理仿真环境，包括电磁学、结构力学、声学、流体、热或化学分析。二重求和的表达式不仅限于几何模拟，还可用于材料数据、方程系数、边界条件模拟等。使用这个方法，可以在循环中使用大量表面来收集结果的统计信息。

将二重求和推广为三重求和，可以合成 3D 非均匀材料数据。但是，在为 3D 模拟进行三重求和时，必须做好耗时和占内存的计算准备。

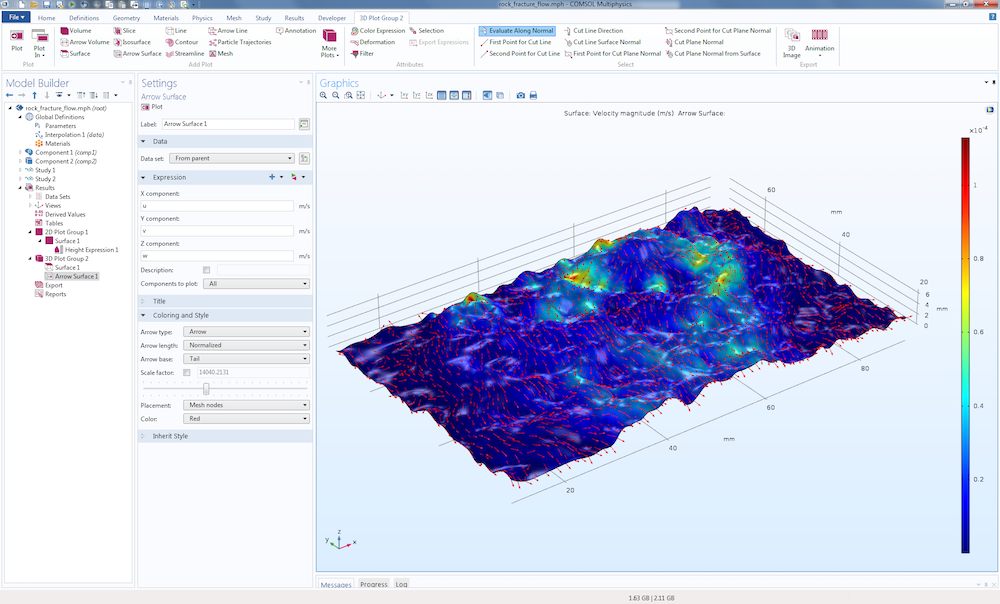
基于合成生成的裂缝孔径数据的裂缝流动模拟。岩石裂隙流模型是 COMSOL Multiphysics案例库中 的一个教学模型。

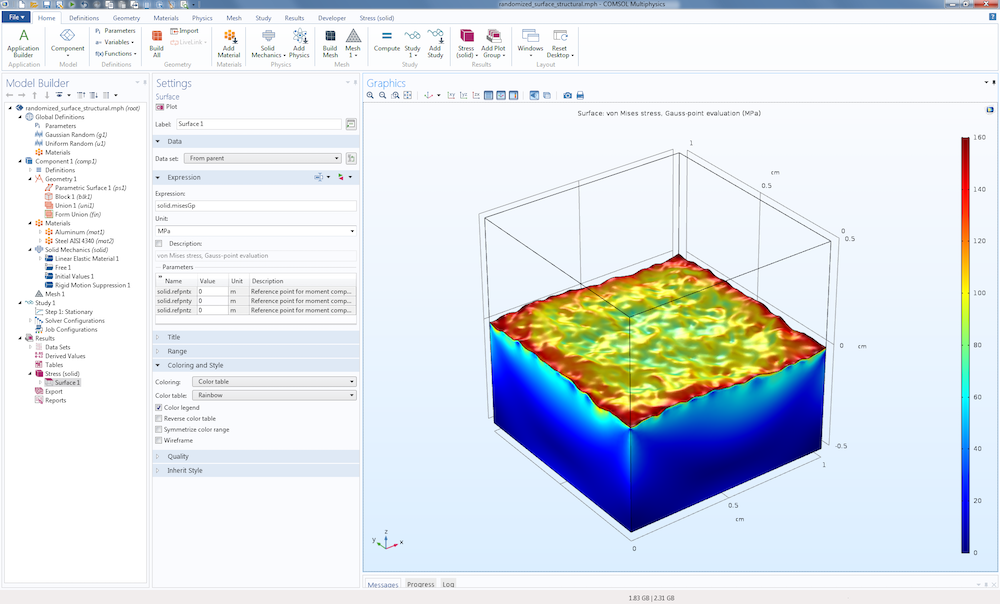
基于本文中描述的参数化表面，对两个带材料界面的 1 厘米大小的金属块进行通用热膨胀分析。底部材料板是铝，顶部材料板是钢。可视化图显示了材料界面和铝板表面的 von Mises 应力。

离散余弦与傅里叶变换的关系

对下式求和

类似于离散余弦变换或离散傅里叶变换的实部：

式中，下标 c 表示复数，x 和 y 现在采用离散值。这里，用复数傅里叶系数编码相位角信息。

根据离散傅里叶变换的定义，我们可以进行索引变换，生成我们更熟悉的下列形式：

或使用离散值：

更常见的离散傅里叶变换的索引如下所示：

其中，

请注意，为了生成实值数据，傅里叶系数需要满足共轭对称关系，以消除正弦函数的虚值贡献。使用余弦函数的总和（即余弦变换）可以避免这个问题。

生成大量傅里叶系数的快速方法是使用快速余弦变换(FCT)或快速傅里叶变换(FFT)。这可以在另一个程序中完成，然后作为一个插值表格导入 COMSOL Desktop^® 用户界面。上述三角插值方法计算较慢，但优点是可以直接在非结构化网格上使用，并且只需在用户界面中细化网格就可以自动细化。

有关使用 FFT 合成表面的说明，请参见参考文献1。

一维和圆柱体示例

最后，我们来看看在 COMSOL Multiphysics 中由随机表面生成的几个有趣的特殊示例，包括曲线和圆柱体。

随机曲线

在 2D 仿真中，可以使用以下表达式生成随机曲线：

0.01*sum(if((m!=0),((m^2)^(-b/2))*g1(m)*cos(2*pi*m*s+u1(m)),0),m,-N,N)

其中， g1 和 u1 是一维随机函数。

请注意，在生成曲线时，与“相同随机水平”的表面相比，谱指数的值较低。

谱指数为 0.8 的随机曲线。

随机极曲线

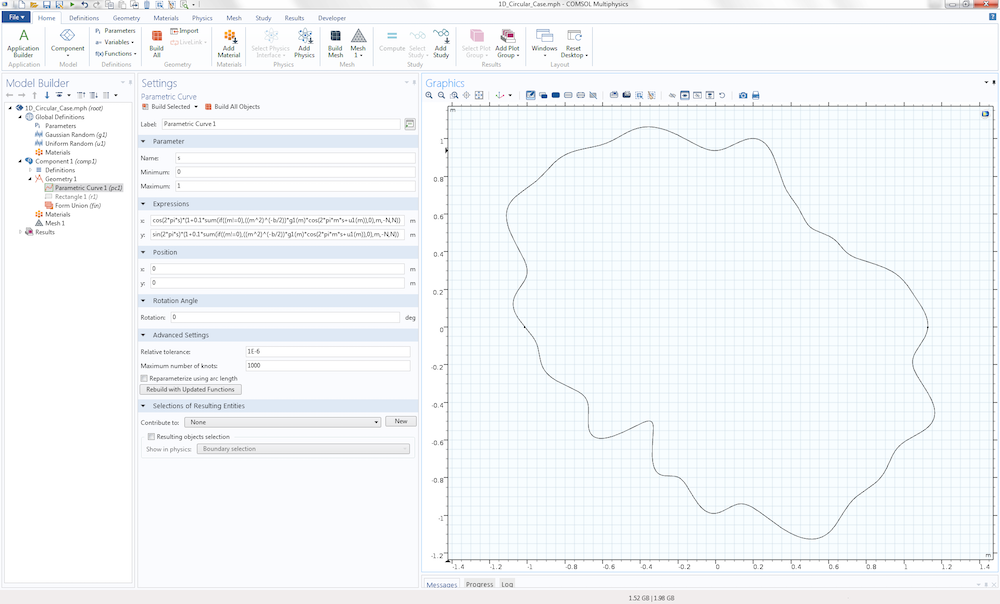
可以在极坐标中生成一条表示圆的随机偏差的随机曲线：

x=cos(2*pi*s)*(1+0.1*sum(if((m!=0),((m^2)^(-b/2))*g1(m)*cos(2*pi*m*s+u1(m)),0),m,-N,N))

y=sin(2*pi*s)*(1+0.1*sum(if((m!=0),((m^2)^(-b/2))*g1(m)*cos(2*pi*m*s+u1(m)),0),m,-N,N))

对应于二维极坐标中的参数曲线：

谱指数为 0.8 的随机极曲线。

随机圆柱体

可以使用参数化曲面生成一个 3D 随机圆柱体，参数如下：

x=cos(2*pi*s1)*(1+0.1*sum(sum(if((m!=0)||(n!=0),((m^2+n^2)^(-b/2))*g1(m,n)*cos(2*pi*(m*s1+n*s2)+u1(m,n)),0),m,-N,N),n,-N,N))

y=sin(2*pi*s1)*(1+0.1*sum(sum(if((m!=0)||(n!=0),((m^2+n^2)^(-b/2))*g1(m,n)*cos(2*pi*(m*s1+n*s2)+u1(m,n)),0),m,-N,N),n,-N,N))

z=s2*2*pi

其中，参数 s1 和 s2 在 0 和 1 之间变化。

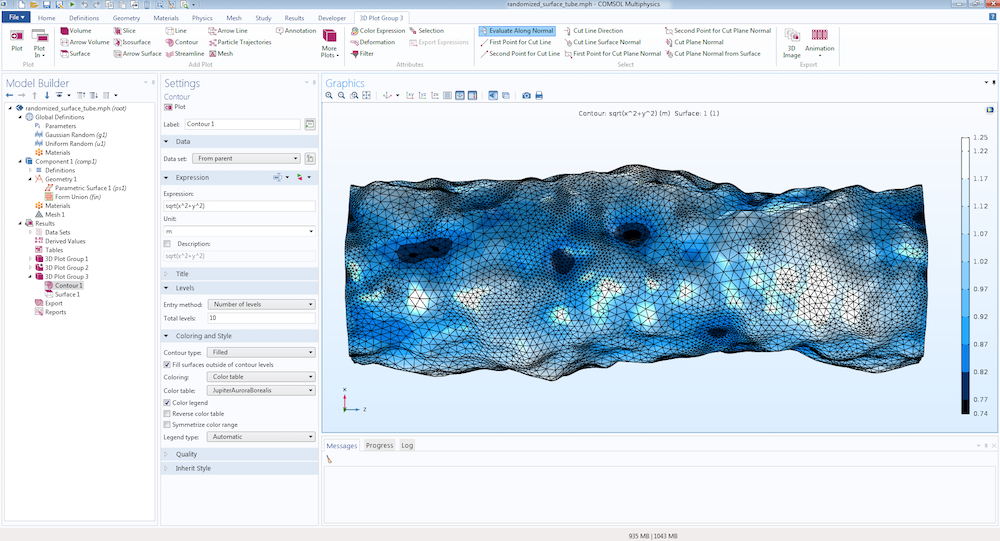
对应于圆柱坐标中的参数化曲面：

这种单一随机圆柱体代表一种自相交表面，这在 COMSOL Multiphysics 中是不允许的。我们可以通过创建对应于参数 s1 的四个补丁表面来轻松解决此问题，这些补丁表面的范围在 0 ~ 0.25、0.25 ~ 0.5、0.5~ 0.75 和 0.75 ~ 1.0 之间。一个这样的补丁对应于大小为 \frac{\pi} {2} 的极角跨度。

使用极坐标的随机管状表面。

COMSOL Multiphysics^® 5.5 版本中的新零件

从 5.5 版本开始，COMSOL Multiphysics 的零件库扩展了几个新零件，包括用于创建随机平面的零件。

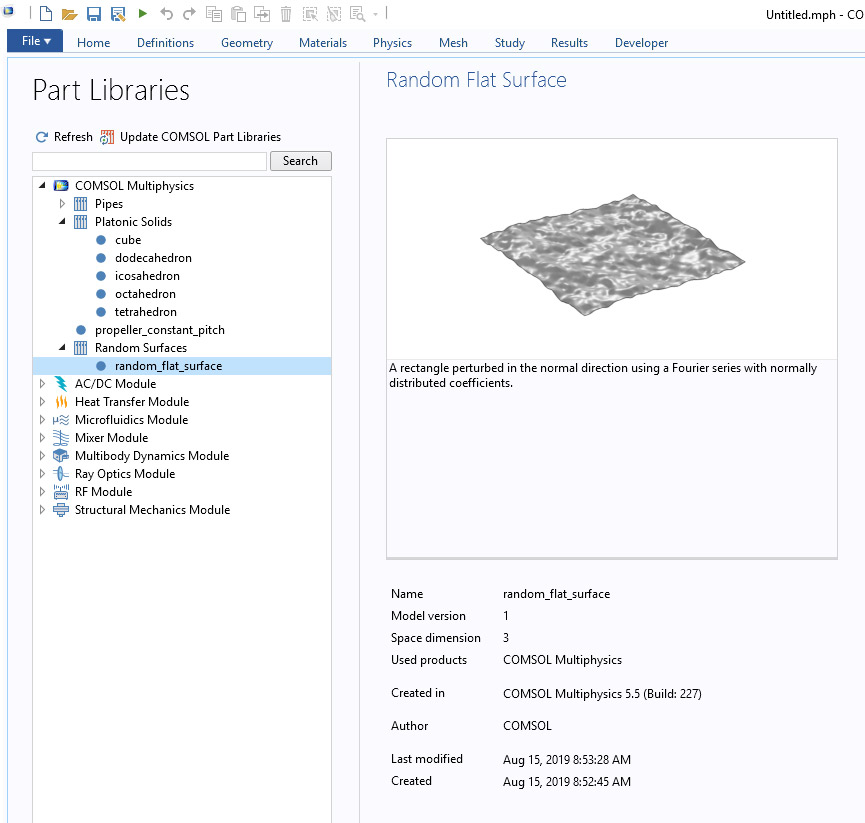
COMSOL Multiphysics 零件库中的 随机平面 零件。

参考文献

• The Science of Fractal Images, Editors: Peitgen, Heinz-Otto, Saupe, Dietmar. Eds.