
磁体中的磁矩动力学可以通过微磁模型描述,即朗道-栗弗席兹-吉尔伯特方程(Landu–Lifshitz–Gilbert equations,LLG)。我们使用 COMSOL Multiphysics® 软件中的“物理场开发器”开发了一个定制的“微磁模块”,可用于在 COMSOL® 软件框架内进行微磁建模。这个定制的微磁模块可以直接与其他附加模块耦合进行多物理场微磁仿真,例如磁-偶极耦合、磁-弹耦合、磁-热耦合等。微磁模块软件包以及用户指南可以在文末提供的网址中下载,欢迎试用。
磁振子学和微磁学导论
磁振子学 是自旋电子学或磁学的子分支领域(参考文献1),类似的还有声子学和光子学。磁振子学更侧重于研究由磁性体系的元激发,即自旋波(或量子极限中的磁振子)携带的能量和信息传输。自旋波可以携带能量、线性动量、角动量,因此可以用来编码信息。由于具有极小的阻尼和无焦耳热等特性(参考文献2),钇铁石榴石 YIG (Y3Fe5O12) 等磁绝缘体是操控自旋波的理想材料。此外,自旋波还可以与磁结构相互作用(参考文献3),例如磁畴壁、磁涡旋和磁斯格明子等,从而为磁存储器的设计和操控提供了一条新途径。这使得磁振子技术有望成为下一代信息技术的候选者。
在这篇博文中,我们将演示如何在 COMSOL Multiphysics 中使用“微磁模块”对自旋波动力学进行数值微磁仿真。
微磁模型简介
磁性材料中磁矩的动力学由 LLG 方程控制。微磁模型的核心是将一个或多个晶胞中的所有磁矩视为一个半经典的宏自旋,用单位向量 \textbf{m} 定义表示为
其中,\textbf{M}(\textbf{r}, t) 是总磁化强度的时空分布函数,M_s 是材料的饱和磁化强度。
该单位磁矩向量的时间演化遵循 LLG 方程(参考文献 4)
其中,点表示时间导数,\gamma 是旋磁比,\alpha 是吉尔伯特阻尼系数,\textbf{H}_{\rm{eff}} 是施加在局域磁矩上的有效场,可以被定义为
其中,\mu_0 为真空磁导率,E 为磁系统的自由能,包括所有可能的相互作用。
假设一种最简单的情况:在沿 z 方向施加的静态磁场中的一个宏自旋。有效场很简单,可以表示为 \textbf{H}_{\rm{eff}}= H \hat{e}_z。从宏自旋稍微偏离平衡 z 方向的初始状态开始,宏自旋矢量根据 LLG 方程按右手定则围绕有效场进动。在吉尔伯特阻尼(以 \alpha 表示)作用下,系统的动能最终消散,宏自旋驰豫到其能量最小值,即与有效场平行。这种进动的动力学与铁磁共振 (FMR) 相关,其进动角频率与外加场的强度呈线性关系。
当引入非局域相互作用时会出现自旋波,例如,在连续极限中采用以下形式的短程交换相互作用 \textbf{H}_{\rm{eff}}=A \triangledown^2\textbf{m},其中 A 为交换刚度系数。存在交换相互作用的情况下,单个宏自旋的进动模式可以传输到相邻的宏自旋,导致角动量流的传播,即自旋波。
电磁波和弹性波以及自旋波都可以通过纳米结构设计进行空间上的限制或调控。此外,自旋波还可以通过磁结构(磁矩在空间中的非均匀分布)来调控,例如磁畴壁,即具有相反磁化强度的两个磁畴之间的过渡区域。理论和实验都表明,磁畴壁可以作为自旋波的传导通道,用于设计可重构的自旋波电路。
微磁仿真不仅可以帮助解释实验结果,也有很多成功的例子表明,该方法可以预测新现象,并通过实验进行验证。
通过物理场开发器开发微磁模块
市场上有两种主流的开源微磁仿真软件:面向对象的微磁框架(OOMMF)和支持GPU 加速的 Mumax3。
但是,我们更喜欢使用 COMSOL Multiphysics 进行微磁仿真。原因有两个:
- COMSOL Multiphysics 基于有限元方法,而不是 OOMMF 和 Mumax3使用的有限差分方法。在对复杂的几何形状和结构进行建模时,有限元方法更加强大。
- 微磁模块可以直接与 COMSOL Multiphysics 中丰富的物理模块一起使用。例如,通过与 AC/DC 模块(电流和电磁场)或 RF 模块(微波)耦合,我们可以模拟磁性材料中的偶极相互作用;将微磁模块与结构力学模块相耦合,可以对磁弹性效应进行建模;而传热模块可用于对磁体中的热效应进行建模。在软件框架内,用户定制物理场和 COMSOL 附加产品之间的多物理场耦合相当简单明了。
对 COMSOL Multiphysics 的微磁模块感兴趣的用户可以将编译后的模块文件 Micromagnetics Module.jar 安装到本地 COMSOL 归档文件夹中,之后在选择物理场时就会出现一个新的物理场接口 Micromagnetics (mm)。
微磁模块 (V1.33) 的用户界面如下图所示。
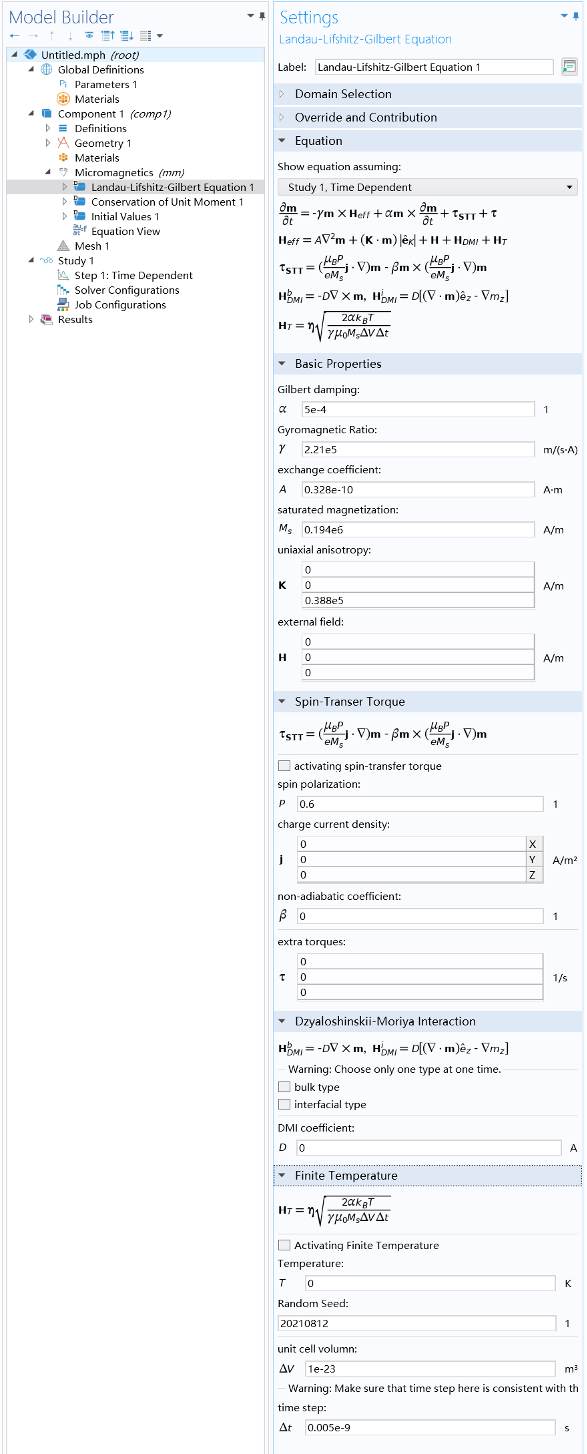
微磁模块(V1.33)具有其他开源微磁仿真软件所具有的几乎所有功能,包括但不限于:
- 基本的 Landau-Lifshitz-Gilbert 动力学方程,包括交换相互作用和单轴各向异性
- 具有适配边界条件的 Dzyaloshinskii-Moriya 相互作用(体类型和界面类型)
- 自旋转移矩(包括场项和力矩项)
- 可输入任意形式的有效场和自旋力矩(可以同时是时间和空间的函数)
- 有限温度效应(可通过自定义随机种子引入随机性)
- 钉扎边界条件和周期性边界条件
- 能够在一个区域内求解多个独立的 LLG 方程(例如可用来模拟具有多个子晶格的人工反铁磁体)
- 多物理场耦合能力,包括磁-偶极耦合、磁-弹耦合、磁-电耦合、磁-热耦合等
基于微磁模块,我们展示了许多有趣的自旋波物理并提出了各种自旋波器件,例如自旋波二极管(参考文献5)、自旋波光纤(参考文献6)、自旋波偏振片和波片(参考文献7-8)以及存算一体化的磁逻辑门(参考文献9)等。
与微磁模块的多物理场耦合
如上所述,COMSOL Multiphysics 的一项优势是附加模块之间的多物理场耦合能力。自旋波可以被磁场、晶格形变、温度梯度等操控。将自旋波与其他激发(如电磁波和弹性波)耦合,获得的系统可以结合两者的优点,产生丰富的物理现象,促进信息的产生和传输。下面,我们将演示基于微磁模块可以完成哪些多物理场耦合。
腔磁振子学(Cavity magnonics)(参考文献 10)是磁振子学和腔量子电动力学 (CQED) 的交叉学科,后者的应用之一是通过操控光子-物质相互作用来实现量子信息处理。腔磁振子学的典型构型是内部放置磁体的微波腔。磁体中的磁矩进动模式与微波腔中的驻波模式或行波模式耦合。这样的系统为研究自旋流的操控和磁矩的非线性动力学提供了一个新的选择(参考文献 11-12)。腔磁系统可以通过耦合微磁模块和射频模块来模拟。对于静磁模拟,并不需要考虑电磁波本身的动力学行为,因此将微磁模块和 AC/DC 模块(磁场)相互耦合就足够了。
自旋力学(spin mechanics)包括磁矩和晶格形变之间的相互作用。在具有磁弹耦合(或磁致伸缩)的材料中,磁化强度(自旋波)在空间和时间上的变化对晶格产生等效力,而晶格形变(弹性波)对磁化强度产生等效场。例如,如下面的动画所示,面内磁化的碟状薄膜被磁场激发,进动的磁化引起磁性薄膜及其衬底的弹性形变,从而辐射弹性波。自旋力学问题可以通过耦合微磁模块和固体力学模块来模拟。
电流自适应磁结构
在金属磁体中,自旋极化电流对局域磁矩施加自旋转移矩,使得磁结构能够被电流驱动。由于各向异性磁阻 (AMR)的存在,磁性薄膜内的电导率取决于局域磁化强度和电流方向的相对取向,因此可以使用微磁模块和 AC/DC 模块对电流、自旋转移矩和磁结构之间的相互作用进行建模。
如下面的动画所示,施加在两个电极上的电压通过自旋转移矩改变磁结构的空间分布(上图),进一步改变局域电导率和电流密度分布(下图)。在电流的持续作用下,磁结构最终演化至稳定的构型,使得两个电极之间的电导增加。有研究表明这种正反馈行为可用于类脑计算(参考文献13)。
如何获取微磁模块
您可以通过以下方式免费下载微磁模块文件:
下载的压缩文件包括模块安装文件,以及带有安装说明和示例的用户指南。我们非常欢迎和感谢用户的任何建议、报告和交流。更多功能将在未来版本中及时更新。
致谢
作者对复旦大学肖江教授的指导和复旦大学微纳电子器件与量子计算机研究院的支持表示感谢。
关于作者
余伟超本科毕业于同济大学物理科学与工程学院应用物理学专业,获理学学士学位,后赴复旦大学物理学系理论物理专业直接攻读博士研究生,获理学博士学位,曾任复旦大学物理学系博士后研究员、日本东北大学金属材料研究所助理教授,现任复旦大学微纳电子器件与量子计算机研究院青年研究员。余伟超博士的研究兴趣包括自旋电子学和磁学基本现象的理论研究、磁结构和自旋波的动力学、以及磁系统与其他多物理系统之间的耦合,如微波腔自旋电子学(磁子和光子之间的耦合)和自旋力学(自旋波和弹性波之间的耦合)等。他提出并设计了新型自旋电子器件和基于磁性体系的非常规计算概念,例如基于磁系统的存算一体逻辑门和具备自主学习功能的类脑计算架构。他还开发了基于有限元方法的微磁仿真模块,具有与其他多物理场系统双向耦合的能力,有助于基础磁学的研究和新型自旋电子器件的设计。
参考文献
- A. Barman et al., The 2021 Magnonics Roadmap, J. Phys.: Condens. Matter, vol. 33, no. 413001, 2021.
- A. V. Chumak et al., Magnon Spintronics, Nature Physics, vol. 11, no. 453, 2015.
- H. Yu, J. Xiao, and H. Schultheiss, Magnetic Texture Based Magnonics, Physics Reports, vol. 905, no. 1, 2021.
- V. G. Bar’yakhtar and B. A. Ivanov, The Landau-Lifshitz Equation: 80 Years of History, Advances, and Prospects, Low Temperature Physics, vol. 41, no. 663, 2015.
- J. Lan, W. Yu, R. Wu, and J. Xiao, Spin-Wave Diode, Phys. Rev. X, vol. 5, no. 041049, 2015.
- W. Yu, J. Lan, R. Wu, and J. Xiao, Magnetic Snell’s Law and Spin-Wave Fiber with Dzyaloshinskii-Moriya Interaction, Phys. Rev. B, vol. 94, no. 140410, 2016.
- J. Lan, W. Yu, and J. Xiao, Antiferromagnetic Domain Wall as Spin Wave Polarizer and Retarder, Nature Communications, vol. 8, no. 178, 2017.
- W. Yu, J. Lan, and J. Xiao, Polarization-Selective Spin Wave Driven Domain-Wall Motion in Antiferromagnets, Phys. Rev. B, vol. 98, no. 144422, 2018.
- W. Yu, J. Lan, and J. Xiao, Magnetic Logic Gate Based on Polarized Spin Waves, Phys. Rev. Applied, vol. 13, no. 024055, 2020.
- B. Z. Rameshti, S. V. Kusminskiy, J. A. Haigh, K. Usami, D. Lachance-Quirion, Y. Nakamura, C.-M. Hu, H. X. Tang, G. E. W. Bauer, and Y. M. Blanter, Cavity Magnonics, ArXiv:2106.09312 [Cond-Mat], 2021.
- W. Yu, J. Wang, H. Y. Yuan, and J. Xiao, Prediction of Attractive Level Crossing via a Dissipative Mode, Phys. Rev. Lett., vol. 123, no. 227201, 2019.
- W. Yu, T. Yu, and G. E. W. Bauer, Circulating Cavity Magnon Polaritons, Phys. Rev. B, vol. 102, no. 064416, 2020.
- W. Yu, J. Xiao, and G. E. W. Bauer, A Hopfield Neural Network in Magnetic Films with Natural Learning, ArXiv:2101.03016 [Cond-Mat], 2021.




评论 (95)
鹏浩 李
2021-11-02您好,请问怎么将Micromagnetics Module.jar 安装到本地 COMSOL 归档文件夹中?谢谢
伟超 余
2021-11-02你好,直接将该jar文件直接复制到安装目录下plug-in文件夹中即可,详情请参照附带说明书中的安装方法
鹏浩 李
2021-11-03您好,请问可以用这个模块仿真铁磁共振吗?想仿真一个块状YIG铁磁共振的过程。非常感谢!
伟超 余
2021-11-03可以的,铁磁共振是微磁学模型的一个最经典的应用之一,详情请参考说明文档以及其所引用的参考资料
鹏浩 李
2021-11-03您好,我今天一直在看您的文档,请问您这个模块铁磁共振仿真的结果是和Mumax一样输出包含磁矩行为的文件然后到matlab里进行FFT吗?
伟超 余
2021-11-03对的,可以将数据导出做数据处理,也可以直接在COMSOL内部做各种后期处理
鹏浩 李
2021-11-03您有铁磁共振这方面的模型吗?想参考一下,您文档里的引用文献有些看不太懂,谢谢老师!
伟超 余
2021-11-04示例文件还在准备制作中,你可以在本博客提供的外链中找到并访问肖江教授课题组网站,下载我的博士论文,相对于英文文献更容易理解一些
鹏浩 李
2021-11-04好的老师,非常感谢!
鹏浩 李
2021-11-05老师您好,请问导出的数据就是xyz三个方向上的分量吧?我想看材料的铁磁共振吸收峰,怎么在comsol内部进行处理呢?麻烦您了,谢谢老师
伟超 余
2021-11-05COMSOL内的数据处理请参考官方教程,你可以导出数据用你自己熟悉的编程工具进行处理
鹏浩 李
2021-11-07老师您好,请问在您的模块中输入外加场H时,比如我x方向输入一个微扰场,z方向输入一个偏置场,输入时偏置场只能输入一个固定的值吗?可不可以输入一个范围,从多少A/m到多少A/m,谢谢老师!
伟超 余
2021-11-07输入值可以是时间或空间的函数,我想你的意思应该是执行多次仿真,每次仿真用不同的参数,这种情况推荐使用COMSOL的参数化扫描功能。
鹏浩 李
2021-11-11老师您好,我用您的模型已完成铁磁共振扫频仿真,请问可以仿真扫场吗?扫场操作的外场我不是太清楚该怎么加,现在在z方向上加的偏置场都是一个定值,怎么添加一个带有范围的偏置场呢?麻烦您了
伟超 余
2021-11-11你可以在参数里定义一个新的变量,比如说是dH,那么磁矩的有效场就是H+dH。在使用参数化扫描的时候就可以对dH的范围进行设置从而扫场,参数化扫描的方法请参考COMSOL自带的教程。
鹏浩 李
2021-11-11好的,谢谢老师
鹏浩 李
2021-11-30余老师您好,请问在用您的模块和其他模块比如RF模块耦合时,需要考虑网格匹配的问题吗?RF求解麦克斯韦方程组,是宏观的,自适应划分的网格会不会和微观的微磁模拟不匹配,这时是不是需要手动设置来给网格大小划分一个范围
伟超 余
2021-11-30最好能够手动设置一下网格,磁性材料以及磁性材料与宏观空间的连接处最好划分得细一些,在远离磁性材料处可以采用默认的RF模块网格划分。记住一个原则就行:网格大小取决于物理场的特征尺度。
鹏浩 李
2021-11-30老师您好,我在参考您Spin Cavitronics例子是集总端口设置总是报错,提示“均匀集总端口应该放在两个导电边界之间”,您这个例子有相关教程吗?谢谢老师!
伟超 余
2021-12-01集总端口设置并不是微磁学模块包含的内容,你可以学习一下RF模块的相关案例以及翻看RF模块的说明书,关于集总端口要怎么设置,COMSOL自带的很多模型里就有集总端口你可以直接拿来用
水华 张
2021-11-10您好,我按照您说明书中的操作将jar文件直接复制到安装目录下plug-in文件夹,也开启了物理场开发器,为什么没看到micmagnetic模块呢?是还有其他操作吗?
伟超 余
2021-11-10你好,复制完之后需要重启软件,另外也请注意一下版本号,本模块针对的是COMSOL5.6,若版本不对也可能无法安装
水华 张
2021-11-10老师,您好。我用的就是5.6的COMSOL,软件也重启了,但还是没有新的物理场添加。跟您确认一下是将您在交流区的压缩文件下载,转成.Jar文件再复制到安装目录吗?
伟超 余
2021-11-10模型交流区的zip文件下载后需要解压,解压后将其中一个名为“Micromagnetics Module”的无扩展名文件手动加上扩展名jar再复制到软件安装目录下。你也可以尝试从其它几个渠道直接下载模块文件,COMSOL模型交流区由于禁止jar文件上传才需要多此一步操作。
水华 张
2021-11-11问题已解决,非常感谢您的帮助。
水华 张
2021-11-16老师,您好。我想用您的模型模拟外界磁场下铁磁质磁畴的偏转,主要关心的是磁畴的偏转角度。请问一下外界磁场的输入,需要和COMSOL自带的AC/DC模块中”磁场无电流”耦合还是直接用微磁模块中的外界磁场进行定义?另外,我所关心的磁畴偏转角度的输出是输出变量α吗?
伟超 余
2021-11-16如果你要考虑磁矩之间的偶极相互作用,那么需要与AC/DC模块中的“磁场无电流”进行耦合,若只考虑交换相互作用和磁晶各向异性,那么本微磁模块就足以模拟。在本模块中alpha指代的是Gilbert damping系数,与磁畴偏转角度无关。你可以导出磁畴壁三个分量(mx,my,mz)的空间分布来计算偏转角度。
水华 张
2021-11-17老师,您好,非常感谢您的回答,我按您说的进行了计算,发现了几个问题,麻烦您帮忙看一下。我参考了您users guide里微磁和AC/DC 的耦合案例进行了建模,但是计算出现了一些问题。1、瞬态研究一直提示”找到未定义的值“(我的参数是按照您模型定义的)2、我自建的模型进行计算的时候AC/DC物理场计算顺利,但微磁物理场进度条一直在0%,而且从收敛图上看到收敛性一直在下降 3、两个模型的稳态研究都比较顺利,但导出的mX,mY,mZ和初始值一样,并没有变化。
伟超 余
2021-11-171. 请确认你的求解域设置是否正确。内部小球为磁性材料,需要同时求解LLG方程和麦克斯韦方程,外部大球为空气层,只需要求解麦克斯韦方程。2. 进行多物理场耦合的时候微磁学模块与AC/DC模块同时运行,我不太理解如何做到一个模块计算顺利另外一个模块进度为零。3. 本微磁学模块求解的是动态LLG方程,因此不能用来进行稳态研究,稳态研究理当无计算结果。
伟超 余
2021-11-23该模块的使用介绍以及视频案例展示已上传至b站:
https://www.bilibili.com/video/BV1EL4y1p7bN/
案例库及教程将不定期更新,若有想学习了解的案例请留言或私信
玉平 姚
2021-12-19余老师,您好,我在安装过程中出现了“初始化物理场接口失败。”的错误,这个该怎么解决呢?是不是因为版本问题,我的版本是5.5
玉平 姚
2021-12-19老师,您好,问题已解决,是版本的问题,可能不支持5.5版本,打扰了,谢谢
Li Jie
2022-01-12老师您好,该模块可以模拟磁珠微粒,比如几微米的FE3O4粒子的团聚吗?
伟超 余
2022-01-12你好,原则上可以的,但是不建议。这个模块关注的是磁体内磁结构的动力学,如果把Fe3O4粒子当做一个单畴粒子来考虑也不考虑其磁矩的动力学性质的话还是建议用COMSOL自带的AC/DC模块更好,否则就是杀鸡用牛刀了。
慧敏 武
2022-03-19你好,我最近也在做磁性微球的团聚模拟,一点头绪都没有,请问可以指导一二吗?
伟超 余
2022-03-20你好,这方面我没有经验,请参见我上面的回复,我并不认为微磁学模块适合用来研究你这个课题,或者你可以分享一下一篇经典的文献,我判断一下是否可以做
立军 刘
2022-03-21您好,请问可以模拟钕铁硼材料进行多级充磁过程吗?
伟超 余
2022-03-21你好,永磁体的充磁过程从物理上来说和一块磁性样品被磁场磁化没有什么区别,所以原则上可以模拟。但是永磁体充磁的过程对应的过程能量尺度比较大,永磁体的矫顽场也远大于普通的磁性材料,所以基于LLG方程的微磁学模型是否适用对我来说是个问号,还是建议你参考你们领域里常用的数值方法进行模拟。
立军 刘
2022-03-22好的,谢谢。
Luke Feng
2022-03-24老师,请问用这个模块可以做纤维的磁阻抗模拟吗?解析解是通过LLG方程和Maxwell 方程共解得到
伟超 余
2022-03-24我对这个领域不了解,如果理论模型是基于LLG方程和麦克斯韦方程的话那这个模块可以求解的,详情你可以参考我在b站的教学视频,或者可以分享一下文献我进一步判断需要怎么建模
Luke Feng
2022-04-06好的,谢谢老师
静 徐
2022-05-10老师您好,请问在一个物理场 Micromagnetics下添加两个LLG方程与用户手册中提到的两个物理场Micromagnetics的耦合有什么区别吗?因为仿真中需要对不同晶格指定不同材料,我目前是用前一种方法,在微磁物理场下添加了两个LLG方程,因为这方面接触不太多,不太清楚这样做是否合理?
伟超 余
2022-05-10用第一种方法是无法进行仿真的,原因在于这两套LLG方程属于同一个微磁学模块,因此存在竞争关系,若你对某块区域定义了相应的LLG方程,那么另一组LLG方程就无法再在该区域定义。一个可行的做法就是引入两个微磁学模块,相当于求解两套独立的LLG方程。具体你可以参考我的一期视频教程:https://www.bilibili.com/video/BV1EL4y1p7bN?p=7,有问题也可以在视频下方留言提问讨论
伟超 余
2022-06-02微磁学模块V2.01已经更新,新版本中包含了全新的频域求解功能,更多详情请参见用户手册。模块可至模型交流区下载,https://cn.comsol.com/community/exchange/883/,演示视频和讨论可在我的B站主页进行https://www.bilibili.com/video/BV1EL4y1p7bN/
章 王
2022-07-16老师 您好,我最近在做有关ME(压电、磁致伸缩)复合材料的仿真,主要目的是想通过在压电材料上施加电压,使压电材料产生振动,将这个振动传递到磁致伸缩材料上,使磁致伸缩材料中的磁矩产生相应的振动,从而在材料中辐射出电磁波,想问问您的微磁模块能够做这方面的仿真吗?
伟超 余
2022-07-16你好,可以的,需要将微磁学模块和固体力学模块以及rf模块耦合就可以,可以参考我在b站的视频
章 王
2022-07-17谢谢老师,我想再问一下,您的微磁模块解的是LLG方程,求解出的是模型中的磁矩,然后我在使用comsol中自带的磁致伸缩模块中,该模型中需要用户定义的弹磁模型是应力-磁化或者应变-磁化,即需要定义弹磁材料的弹性矩阵和压磁耦合矩阵,但如果是用您的微磁模块,那么材料模型如何定义呢?(抱歉老师,因为我不是很懂LLG方程),或者说是否能够从弹性矩阵和压磁耦合矩阵得到您微磁和固体力学耦合所需的材料参数?谢谢老师的解答
伟超 余
2022-07-17你问的是一个很好的问题,通常的磁致伸缩模型给出的是磁矩和应力之间的响应关系,通常是线性的(当然非线性的模型会更复杂),而使用微磁学模型来描述磁弹耦合那么本身就是非线性的,可以说更加微观,此时磁矩的动力学由LLG方程描述,固体的形变动力学由对应的虎克定律描述,两者之间的用磁弹耦合相互作用来描述(mageto-elastic coupling),具体的模型可以参考这篇论文:https://doi.org/10.1103/PhysRevB.104.014403,也就是说使用包含磁弹耦合的微磁学模型是可以导出通常的磁致伸缩唯象模型,但是反向却不可以
章 王
2022-07-17谢谢老师的讲解,因为我是电磁场方面的学生,可能对您推荐的这篇文章不是很熟悉,您这篇论文是讲如何定义我所需要的材料参数的吗?或者换句话说,我现在有一块材料,是具有磁致伸缩性质的,如何得到建立这块材料的非线性的微磁学模型的材料参数呢?还有一个问题,由逆压电效应产生的振动频率可能偏低,从而导致磁矩振动频率也偏低,那么如果直接和RF模块耦合的话是否计算消耗内存太大导致无法计算,您的微磁模块能够和低频电磁场模块进行耦合从而计算出空气中的电磁场分布吗?谢谢老师的解答
伟超 余
2022-07-17第一个问题:我并没有太看明白你的问题,我并不知道你需要哪些参数。如果要用微磁学模块求解磁弹问题,那就需要知道材料的磁性性质(交换相互作用、饱和磁化强度、各向异性等),以及材料的弹性性质(例如lame常数和质量等),除此之外还需要知道磁弹耦合常数b1和b2,这些参数可以查文献获得,也可以从实验中测量得到。
第二个问题:和多个模块耦合确实会造成计算量很大的问题,因为这些物理场属于不同的尺度,无法避免。该微磁学模块可以与AC/DC模块耦合计算空气中磁场分布,这些信息你可以从用户手册和B站视频案例中获取。
章 王
2022-07-17好的老师,其实我的问题就是求解弹磁问题,那么我仿真中遇到的问题就是不知从何处能查到您描述的这些材料参数,您是否可指点迷津,就如我最开始所说,我如果想要从宏观来看弹磁效应,即磁致伸缩,这时有描述其线性行为的弹性矩阵和压磁耦合矩阵,若想从较为微观的磁矩的运动来看,此时模型为非线性,就像您说的那样,这时需要的描述材料参数我不知在何处获得。
伟超 余
2022-07-17可以通过查找文献获得,例如我之前给你的参考文献,里面就有具体材料的参数,然后你可以顺藤摸瓜去找寻你所研究材料的磁弹参数
章 王
2022-07-17万分感谢余老师!!
国凯 徐
2022-08-23余老师,您好。您的视频教程里面讲了“磁场,无电流”与“微磁学,时域”这两个模块的耦合,通过在“磁场,无电流”设置磁化来实现。我现在想实现“电磁波,频域”与“微磁学,频域”的耦合,但是“电磁波,频域”中不能直接设置磁化,只能设置相对磁导率。这个问题要如何解决呢?
伟超 余
2022-08-23你好,微磁学模块与电磁波模块的频域耦合仍然是一个待解决的问题,目前无法实现,这也是我们下一步工作的重点
成超 胡
2022-09-14您好 余老师!非常棒的工作呢!我是做磁性材料的相场模拟的,想请教您两个问题:1.如何在微磁学模块里面加某一区域加磁场(如一块边长100nm的正方体磁性材料,在z轴以5nm为半径往下加100Oe的磁场)?2. 如何以生成的文件(x y z mx my mz)作为初始值进行LLG演化呢? 非常感谢!!!
伟超 余
2022-09-14你好,第一个问题:微磁学模块的接口都支持变量输入,例如外场可以限定空间施加范围,如100[Oe]*(x<100[nm])等等,你所需要的构型需要写出圆的参数方程。还有一种方法就是先划分好几何,然后利用变量dom,例如令你所需加磁场的区域的dom为1,那么只需输入100[Oe]*(dom==1)即可。第二个问题:初始值可以自行写解析表达式规定,也可以从之前的求解结果中继承,也可以从外部数据集导入通过插值后赋给初始值,详细的方法可以参考我在B站上的视频https://www.bilibili.com/video/BV1EL4y1p7bN?p=6&vd_source=0aa6b80d49070c8aa03d920aa1cdaf8d,其中P6斯格明子有介绍到上述方法。
金峰 邱
2022-10-03您好,余老师,我是一个建模爱好者,咨询下,我在一个气液倒流的多相反应器中间,放置了一段的多孔介质,但是这些多孔介质带有一定的弱磁性,其数量200多个,每个介质表面的磁场强度大概1-3mT,请问下怎样设置?才能使我的填料上面都带有磁性。
伟超 余
2022-10-05您好,您可以尝试使用COMSOL自带的AC/DC模块,将多孔介质设置成具有磁化强度的磁介质即可
晨 高
2022-11-14余老师您好!请问如果我想要模拟出原本杂乱的微纳薄片在溶液环境下受到磁场作用后翻转至定向排列的过程,请问此模块是否可以用来可视化这个过程呢?
伟超 余
2022-11-14你好,原理上是可以的,但我估计会很复杂。如果你能够模拟带电薄片在电场作用下的运动过程,那么磁场原则上也能做,不过光是前者就已经是很复杂的分子动力学模拟了,再与微磁学模块耦合计算量会非常大
倩 陈
2022-11-17余老师您好,感谢您为微磁学模拟做出的杰出贡献!有个问题想请教您:我想模拟微纳结构之间的磁耦合,看看不同集体激发模式(自旋驻波模式)下磁耦合强度,请问用这个微磁学模块可以实现吗?我尝试了结合磁场无电流模块、微磁学时域模块和频域模块,首先使磁体在磁场无电流模块和微磁学时域模块耦合作用下进行relax,然后把relax的解作为频域模块的初态进行本征频率求解,这样可行吗?我的困惑在于:因为频域不能够直接与磁场无电流模块进行耦合,所以我这样做的话就认为磁矩进动模式对静磁耦合无影响了,似乎也不是很合理。
伟超 余
2022-11-17你好,磁结构之间通过磁偶极相互作用耦合是可以实现的,不过目前我已知的只能在时域中完成。频域模块中将微磁学与电磁场部分耦合也是我们正在探索的课题,理论上频域模块也可以直接和AC/DC模块的频域部分耦合,但如何建模能够得到正确的结果需要经过验证和测试,你的思路和我们的一致,如果你愿意加入探索的队伍的的话欢迎来B站私信我们交流具体实现方案
玉平 姚
2023-02-08余老师您好!目前我的课题需要把微磁学频域模块和AC/DC的频域模块相结合来做一些频域下的计算,在此之前也尝试自己写了一些弱形式方程来计算,可是加入偶极相互作用以后一切都变得超级复杂,单纯用LLG方程和偶极作用方程的弱形式已经超出了我的能力范围,前天在B站上给您留言。您告知我可以用AC/DC的mef模块,但是我需要计算特征频率,因此改用支持特征频率的mf模块,将两个模块耦合以后得到了一些物理结果,我需要计算驻波 模式,但是现有的结果我感觉有些不可靠,能否和你们一起交流下解决方案呢?
伟超 余
2023-02-08你好,这方面我们也做过一些测试,微磁模块和AC/DC模块各自计算特征频率应该都没有问题,耦合后是否还能求解我们还没有尝试过,具体的可以B站私信我们约一个时间腾讯会议交流
奎明 黄
2023-05-25你好,余老师。我想做一个巴克豪森噪声检测的探头仿真模型,检测对象是FeCoV纳米晶铁磁性材料,在交变低频外磁场激励下,铁磁材料由于内部的磁畴壁的不连续或者是不可逆的运动产生了声学上的噪声和磁噪声。我关注的是磁噪声的检测,到时候会用一个检测线圈去检测这个磁噪声。建模的目的是为了查看不同铁磁材料的的巴克豪森噪声特征。请问这个模块可以模拟吗?
伟超 余
2023-05-25你好,应该是可以的,不过这需要磁性材料内有大量的磁畴以及磁畴壁,为了让磁畴的分布有随机性可能还需要引入材料参数的涨落,同时可能也需要考虑温度引入的随机场,利用线圈磁噪声也是可行的,通过与AC/DC模块耦合可以在磁性薄膜外放置一个真实的导线线圈,磁性材料磁矩的变化导致退磁场变化从而导致线圈中的磁通量变化,这些功能微磁学模块都有,不过我预计计算量会特别大不太好操作,你可以先考虑用类似OOMMF那样的有限差分软件,更适合计算你这种物理场空间梯度很大的情形。
奎明 黄
2023-05-26十分感谢老师的回复!相当专业!
爽 陈
2023-06-05老师,您好!我是李鹏老师课题组的陈爽,最近在做磁光耦合所需的超导谐振器的仿真,我按照案例库里的共面波导谐振器设计超导谐振器,在特征值附近扫频算不出谐振峰,物理场的设置我都是和案例库的案例是一样的,请问可能有哪些问题会导致这种情况?非常感谢!
伟超 余
2023-06-05你好,这并不是我的专业领域。如果求解特征值和扫频用的都是同一套模型的话理论上两者应该是一致的。当然不排除实际的超导谐振器几何结构很复杂,会求解出很多或是简并的或是由于数值误差导致的本征值,你在扫频时可以专门扫那些空间分布清晰(电磁波空间分布满足驻波条件)的模式,同时也可以关注特征值中的虚部,通常对应着耗散,如果耗散过大那么线宽也会很宽,会导致你在扫频时观察不到。
爽 陈
2023-06-05好的,谢谢老师
Sun Dongli
2023-08-01余老师,您好,请问从哪里可以下载您的博士论文呢?
伟超 余
2023-10-05你好,可以从以下链接下载
https://www.researchgate.net/publication/369912397_fudandaxueboshixueweilunwen_jiyucijiegoudezixuanbodonglixue_yuweichao
爽 陈
2023-10-05余老师您好,您可否再录一个微波腔自旋电子学的教学视频,您的手册中对这一部分的描述较为简略,有点看不太懂
伟超 余
2023-10-05你好,这一部分内容相对比较进阶,受众面较小,不适合出具体教程。相反地,这种类似的前沿研究内容也不应该以视频教程的方式学习,而是利用文献中提供的资料自行摸索并重复出结果。你可以具体参考我引用的几篇工作,里面的附录提供了所有必要的技术细节。
杜 何
2023-11-03余老师您好!小白入门微磁学这块,也通过您的教程仿真了条状或体状的磁畴壁形成和翻转过程,对于纳米圆环这种结构的磁畴,具有洋葱态和涡旋态,应当怎样设置delta和初始值。
另外comsol微磁学模块和流体粒子追踪可以耦合研究吗~
期望得到您的答复!感谢!
伟超 余
2023-11-03你好,初始值的设置可以自己手写一个解析函数,函数的空间分布和对称性越接近你要研究的磁结构越好。我并不知道你说的delta是什么参数。另外理论上微磁学模块和任何其它模块都一样,可以互相耦合,但前提是耦合方式在物理上是合理且真实的。
杜 何
2023-11-03感谢您的及时回复!应该是theta,就是您在B站磁畴壁那个视频里面的定义变量,应该是theta=2*atan(exp((x-x0)/delta)),这里代表了磁畴壁的的初始位置,我可以理解成这种方程的磁畴壁是沿着特定水平或垂直方向的,我的问题是在于圆环结构的话,要想表现出涡旋态或者洋葱态,应当怎样定义这个变量方程,可能表达得有误,大概意思就是您视频的磁畴壁初始值是条状结构的,想模拟圆环磁畴如何做到
伟超 余
2023-11-05你已经知道了磁畴壁在一维的解析表达式,那么在二维的构型中将其写成洋葱态那样有旋转对称性的形式也不是难事,无非就是将theta表示成空间坐标x和y的函数。如果你是想要问具体的表达式是什么,很遗憾我这里没有现成的,需要你自己推导。
杜 何
2023-12-01余老师您好,我在研究应变耦合下的电控磁,目前一个思路想不清楚。就是我通过压电效应实现了材料的形变,然后怎么去观察他磁畴的变化呢?磁畴的初始值不是自行定义的么,比如定义了一个方向的磁畴壁,该如何去观察他材料在应变前后磁畴的变化呢。还有,接下来我要做的是磁纳米颗粒与材料的耦合,观察材料比如Ni环磁畴壁的旋转移动,操纵了颗粒的运动,这块用微磁学可以实现么?期待余老师的讲解~
伟超 余
2024-01-22你好,考虑了磁弹耦合之后,材料的形变会对磁性体系施加一个有效场,从而使磁畴壁发生的构型发生改变。磁畴应变前和应变后的变化可以直接通过观察磁矩实空间分布得到,但是如果观察不到,则由可能是应变太小或应变有效场太小。这部分内容你可以参考这篇文章:JOURNAL OF APPLIED PHYSICS 119, 113903 (2016)。关于你的第二个问题,微磁学模块耦合AC/DC模块可以给出磁畴壁运动后空间中的磁场分布,有了该信息后就可以模拟纳米颗粒的运动,这一部分还涉及到运动粒子,COMSOL有类似的功能但可能不是其擅长的,COMSOL更擅长对场进行仿真
shubo Hou
2024-01-20老师,您好,请问该模块可以计算晶粒晶界尺度的有限元仿真吗?
伟超 余
2024-01-22应该是可以的,不过这不是我的研究方向。你可以参考这篇文章:Journal of Magnetism and Magnetic Materials
Volume 577, 1 July 2023, 170807,A combined-pole permanent magnet synchronous motor incorporating nanocomposite magnets,之前有一位网友与我讨论过这个问题
shubo Hou
2024-01-20老师,您好,请问该模块可以计算晶粒晶界尺度的相关有限元仿真吗?
梓煊 陈
2024-02-22老师您好!想请问一下能不能实现对某种材料的VNA-FMR测量的S21进行仿真呢?谢谢老师!
伟超 余
2024-02-23你好,可以的,计算S21要用到射频(RF)模块,里面提供了输入输出接口来计算电磁波的透射谱或反射谱。我们需要做的仅仅就是将磁性材料放置于电磁波波导附近就可以,也就是将RF模块与微磁学模块耦合起来。技术细节可以参考这篇论文:Phys. Rev. B 102, 064416(2020)
梓煊 陈
2024-02-23好的好的,谢谢老师!
Jingyu m
2024-03-27老师,您好,请问微磁仿真模块能用在6.1版本上吗,还有一个问题就是这个仿真模块能够进行热磁模拟吗,谢谢您的回复。
伟超 余
2024-03-28你好,该模块可以用在5.6以后的版本。可以模拟热磁效应的,需要将微磁学模块和传热模块耦合在一起,不过具体的测试我们还没有做过,并不能保证方法的正确性
Jingyu M
2024-03-30很感谢您的回复
汇印 吴
2024-04-24您好,请问可以进行AMR效应的仿真吗
伟超 余
2024-04-24你好,可以的,我有一篇相关的论文就是利用微磁模块仿真了AMR的效应 DOI: 10.1103/PhysRevB.104.L180405,手册里也记录了仿真的建模方法。
Kun Wang
2024-04-24你好,请问comsol可以模拟磁针在磁场中的转向吗?如果可以应该用啥模块呢
伟超 余
2024-04-25你好,可以的,甚至用不上这里提到的微磁学模块,只要用到COMSOL自带的AC/DC模块以及固体力学模块即可