从 COMSOL Multiphysics® 软件 5.6 版本开始,半导体模块的薛定谔方程 物理场接口新增了处理多分量波函数的功能。在使用 COMSOL 对半导体器件材料的能带结构进行仿真的博客文章中,我们讨论了如何使用此接口功能处理多分量波函数。本篇博文,我们将以均匀磁场中的硅量子点模型为例,继续探索这项新功能。
量子点简介
量子点是纳米技术中必不可少的组成部分,在太阳能电池、发光二极管(LEDs)、显示器,光电探测器和量子计算中都具有潜在应用前景。Jock 等人最近发表了一篇与自旋轨道量子位的应用领域相关的论文(参考文献1)。他们在该文的补充说明1 中,提供了描述均匀磁场中硅量子点的公式,并在补充图1中显示了数值解。今天,我们将通过仿真的方法来重现该数值解。
硅量子点的薛定谔方程
在参考文献1 的补充说明中,方程1 给出了均匀磁场 \mathbf{B} 中硅量子点的单电子哈密顿量,不包括自旋轨道耦合:
(1)
+\frac{P_y^2}{2 m_\perp}
+\frac{P_z^2}{2 m_\parallel}
+V(\mathbf{r})
+\mu_B \mathbf{B} \cdot \sigma
其中,m_\perp和 m_\parallel 是分别在横向和垂直方向上的有效质量;V 是量子点的约束势能;\mu_B 是玻尔磁子;\mathbf{\sigma} 是 Pauli 矩阵的向量;根据该论文所述,假定旋磁比张量是值为 2 的标量;动量 \mathbf{P} 由下式给出:
(2)
式中,e 是基本电荷,\mathbf{A} 是给定的磁矢势 \mathbf{A}(\mathbf{r})=\frac{1}{2}\mathbf{B}\times\mathbf{r},并且虚数单元 i 前面没有减号,因为 COMSOL Multiphysics 中的所有物理场接口都采用工程符号 exp(-i k x + i \omega t) 而不是 exp(i k x – i \omega t)。
约束势能 V(\mathbf{r}) 项由论文中的等式9 给出:
(3)
+\frac{1}{2} m_\perp \omega_y^2 y^2
+q F_z z
+U_0 \Theta(z)
其中,前两项表示横向各向异性谐波捕获势,其中 \omega_x 和 \omega_y 分别表示在 x 和 y 方向上的捕获势的角频率,第三项描述了一个在 z 方向上的电场势 F_z,q 是粒子电荷(电子 q=-e);最后一项表示在 z=0 的氧化硅界面处存在一个高度为 U_0 的潜在势垒。
参数和变量
建模参数如下表所示:
| 名称 | 表达式 | 值 | 描述 |
|---|---|---|---|
| mxy | 0.19 * me_const | 1.7308E-31 kg | 横向有效质量 |
| mz | 0.98 * me_const | 8.9272E-31 kg | 垂直有效质量 |
| wx | 1[meV]/hbar_const | 1.5193E12 rad/s | x 方向上的捕获势函数的角频率 |
| wy | 3*wx | 4.5578E12 rad/s | y 方向上的捕获势函数的角频率 |
| Fz | 10[MV/m] | 1E7 V/m | 电场 |
| U0 | 3 [eV] | 4.8065E-19 J | 氧化物势垒 |
| B | e_const * hbar_const/2/me_const | 9.274E-24 m2·A | 玻尔磁子 |
| B | 1[T] | 1T | 磁通密度 |
除磁场使用了一个推测值 1[T] 外,所有的参数在论文中均给出。
磁矢势 \mathbf{A}(\mathbf{r})=\frac{1}{2}\mathbf{B}\times\mathbf{r} 使用变量指定,假设均匀磁场指向 y 方向:
| 名称 | 表达式 | 单元 | 描述 |
|---|---|---|---|
| Ax | z*B/2 | Wb/m | 矢量势 |
| Ay | 0[Wb/m] | Wb/m | 矢量势 |
| Az | -x*B/2 | Wb/m | 矢量势 |
物理场设置
薛定谔方程 物理场接口设置了两个波函数,psiu 和 psid,分别对应自旋向上和自旋向下分量:
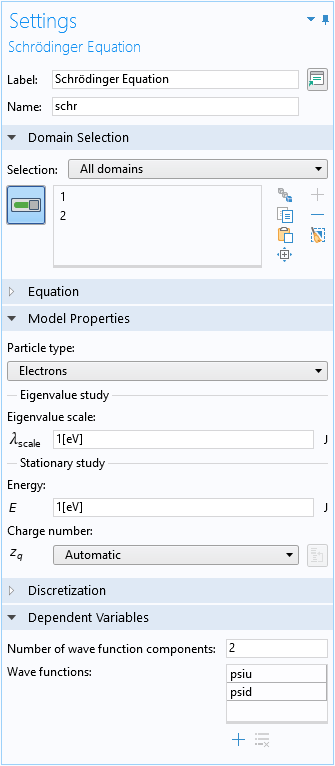
默认的有效质量 域条件用来指定横向和垂直有效质量:
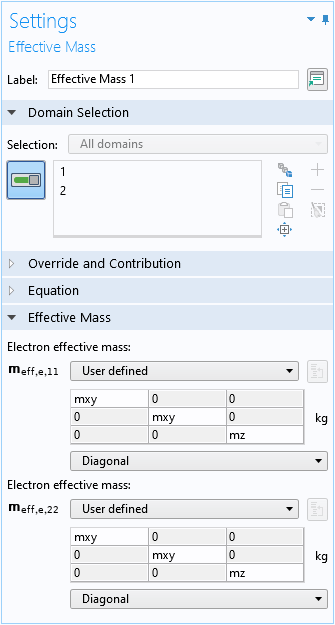
在此模型中,尽管两个波函数分量共享相同的有效质量,但在一般情况下用户界面仍允许不同波动函数分量具有不同的值。
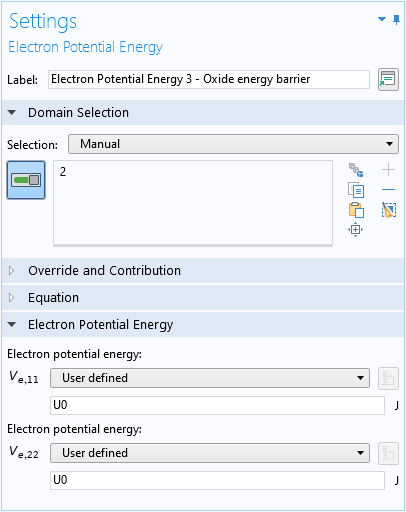
为横向谐波陷波使用三个电子势能 域条件设置约束势能项 V(\mathbf{r})(方程3):
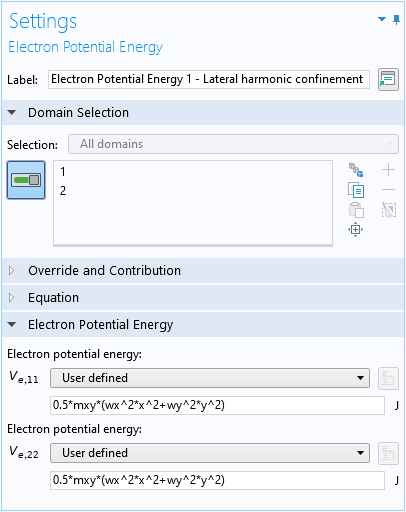
对于电场:
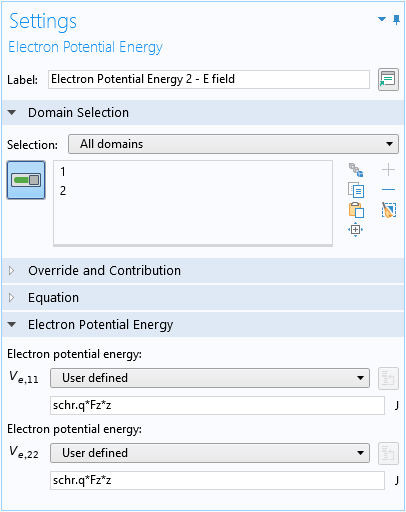
对于氧化物阻挡层:
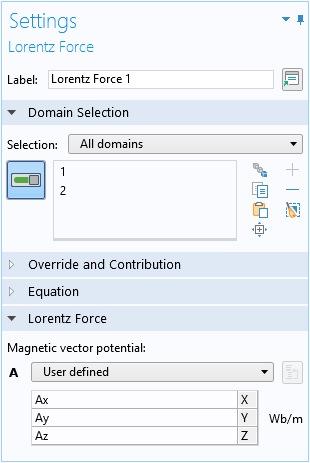
向量势(方程2中的第二项)对动量的贡献是使用洛伦兹力 域条件来模拟的:
最后,利用 零阶哈密顿 域条件实现自旋向上和自旋向下分量的磁耦合(方程1 中的最后一项):
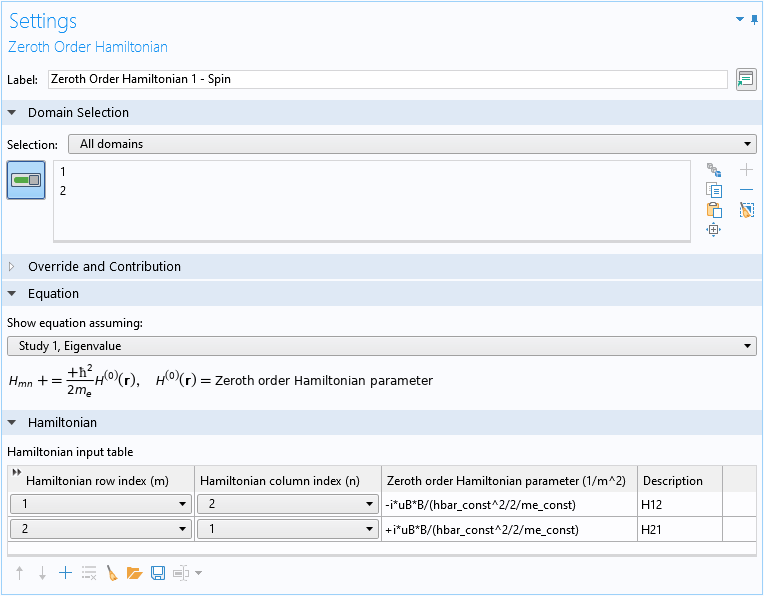
请注意,由于零阶哈密顿 域条件会自动乘以因子 \hbar^2/2m_e,所以在输入表达式时需要除去该因子,以便得到的公式和方程1 的最后一项保持一致:
(4)
= \mu_B B \, \mathbf{n}_y \cdot \mathbf{\sigma}
= \mu_B B \sigma_y
= \left( \begin{array}{cc}
0 & -i\, \mu_B B \\
+i\, \mu_B B & 0 \end{array} \right)
上面的屏幕截图为零阶哈密顿 域条件设置 窗口,哈密顿输入表 的第一行实现了方程 4 矩阵的(1,2)元素,第二行实现了(2,1)元素。
我们还创建了一个简单的扫掠网格,并使用了一个特征值研究来查找前几个特征状态。
理解结果
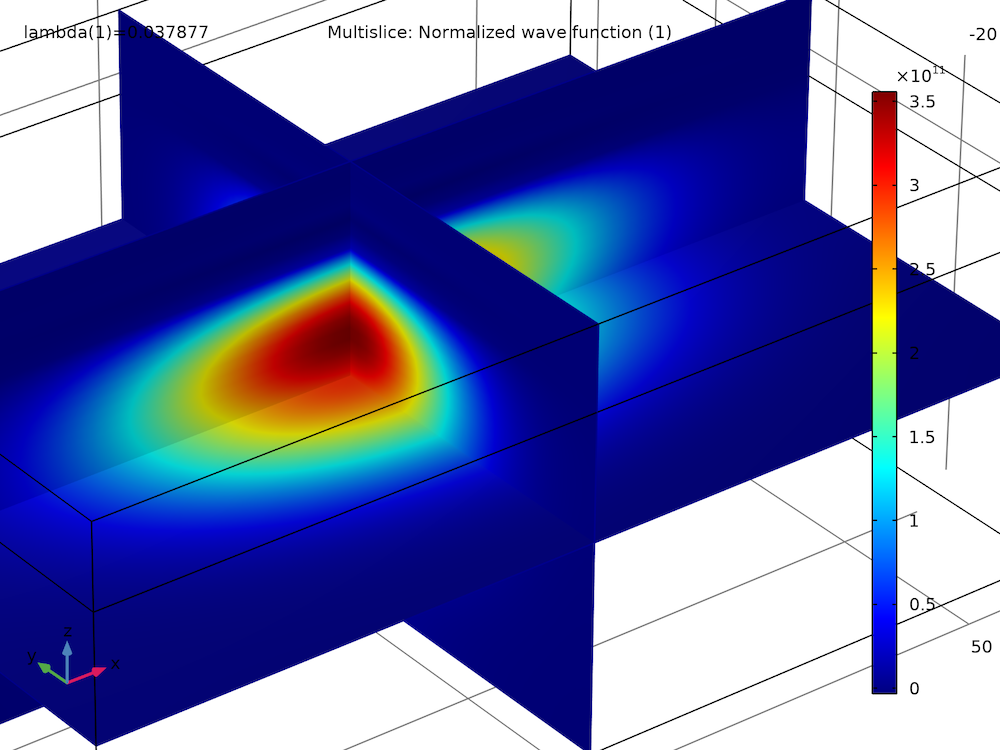
通过绘制前两个本征态的自旋波函数分量的实部和虚部,我们发现它们具有相似的大小和形状,除了一些符号翻转:
| 自旋向上波函数分量 | |
|---|---|
 |
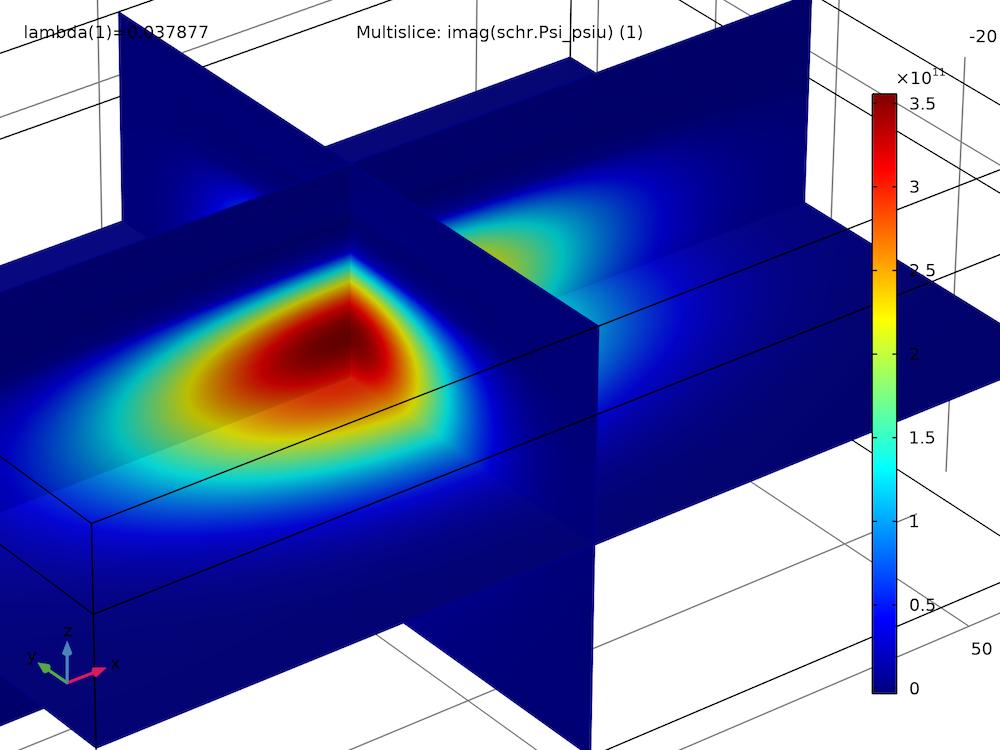
|
| 基态,实部 | 基态,虚部 |
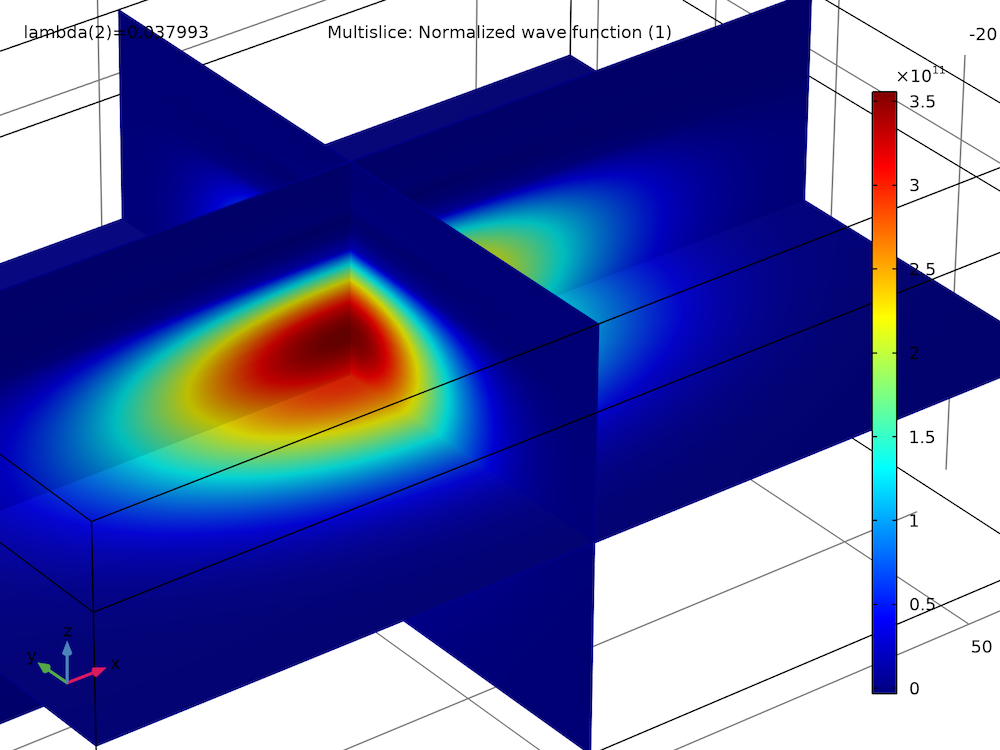
|
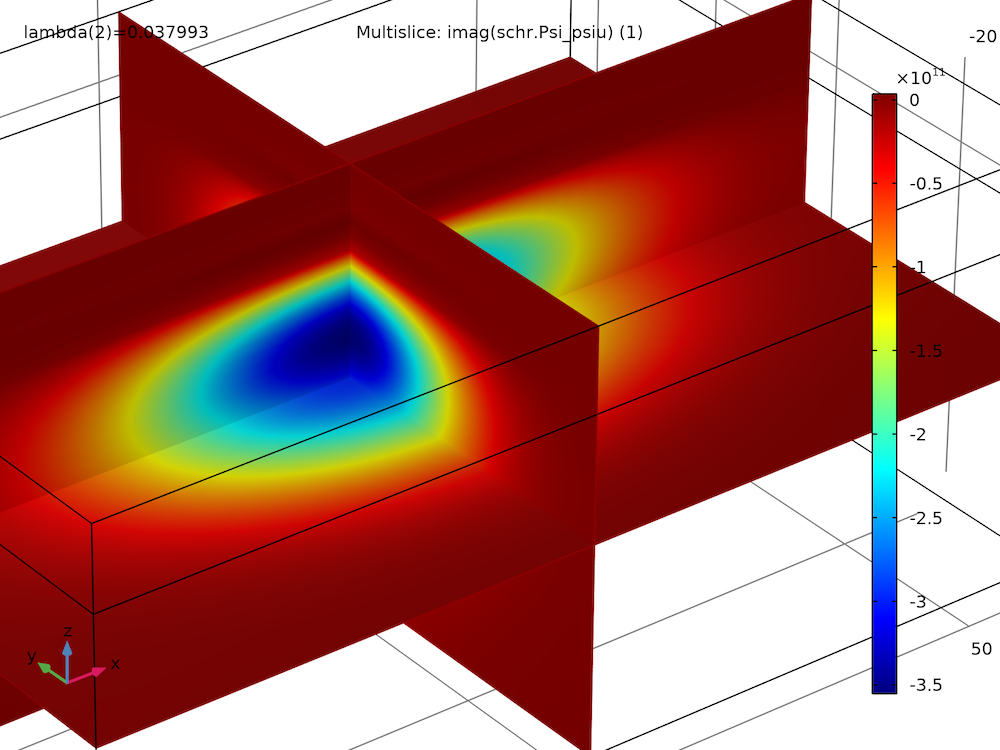
|
| 第一激发态,实部 | 第一激发态,虚部 |
与自旋向上分量相比,自旋向下波函数分量在它们之间也具有这种趋势。
为了理解这一观察,我们评估了峰值密度点附近的波函数分量:
| 特征值 | 向上(1),点:(0,0,-2) | 向下(1),点:(0,0,-2) |
| 0.03788 | 1.000 + 1.000i | 1.000-1.000i |
| 0.03799 | 1.000-1.000i | 1.000 + 1.000i |
可以看出,对于基态(上面结果表的第一行),直到总缩放比例约为 3.6e11 时,自旋分量的幅度为,并且向下旋转分量的幅度为。因此,由两个分量形成的向量与成比例,它被认为是y自旋算子的自旋向下本征态。这与直观的图像一致,即磁场中电子的较低能态的自旋磁矩与磁场平行,因此自旋与磁场反平行。
类似地,对于第一个激发态,直到总缩放比例约为 3.6e11,自旋向上分量的幅值为 1+i=(+i)(1-i),并且自旋向下分量的幅值为 1-i=(1)(1-i)。因此,由两个分量形成的向量与 \left(\begin{array}{c}1\\+i\end{array}\right) 成比例,它被认为是 y 自旋算子的自旋本征态 。这与直观的图片一致,即磁场中电子的高能态的自旋磁矩反平行于磁场,因此自旋平行于磁场。
通过将计算得到的本征态之间的能量差与在均匀磁场下自旋向上和自旋向下的电子之间的预期能量差(2\, \mu_B B)进行比较来进一步确认这一观察结果,利用全局计算得到:
| 特征值 | 计算能量差(meV) | 预期能量差(meV) |
|---|---|---|
| 0.03788 | 0.1158 | 0.1158 |
我们看到前两个本征态之间计算出的能量差和预期的能量差非常吻合——两者的估计值都为 0.116meV。
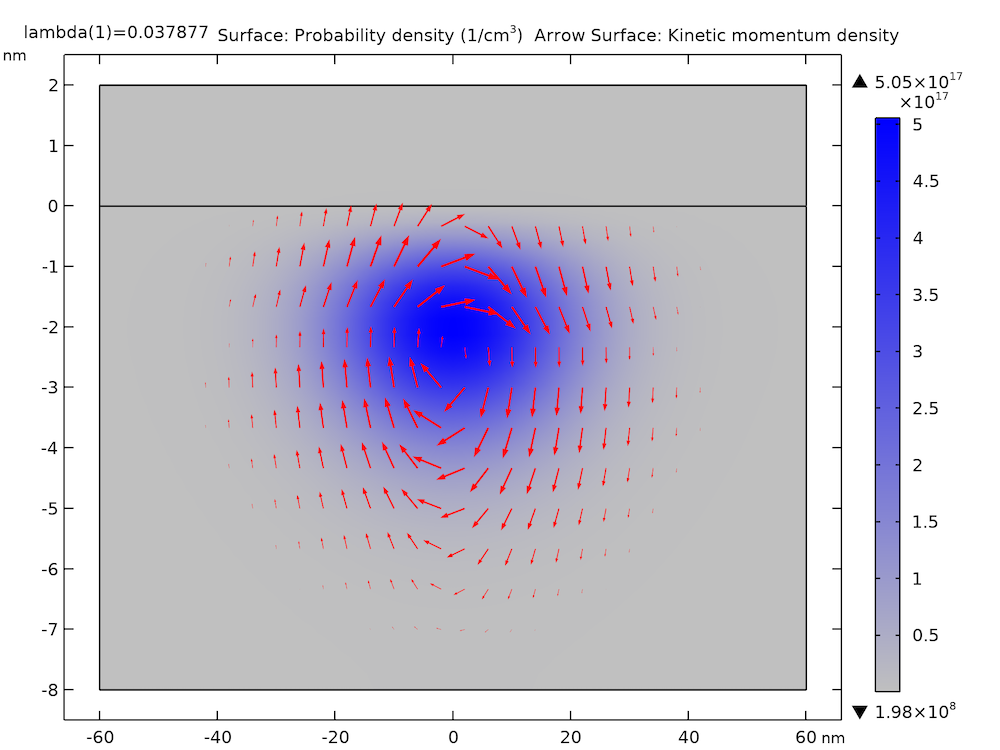
概率密度和动量密度
下图显示了 xz 平面上基态的概率密度(蓝灰色渐变)和动量密度(红色箭头)。它与论文中补充图1较好地吻合。
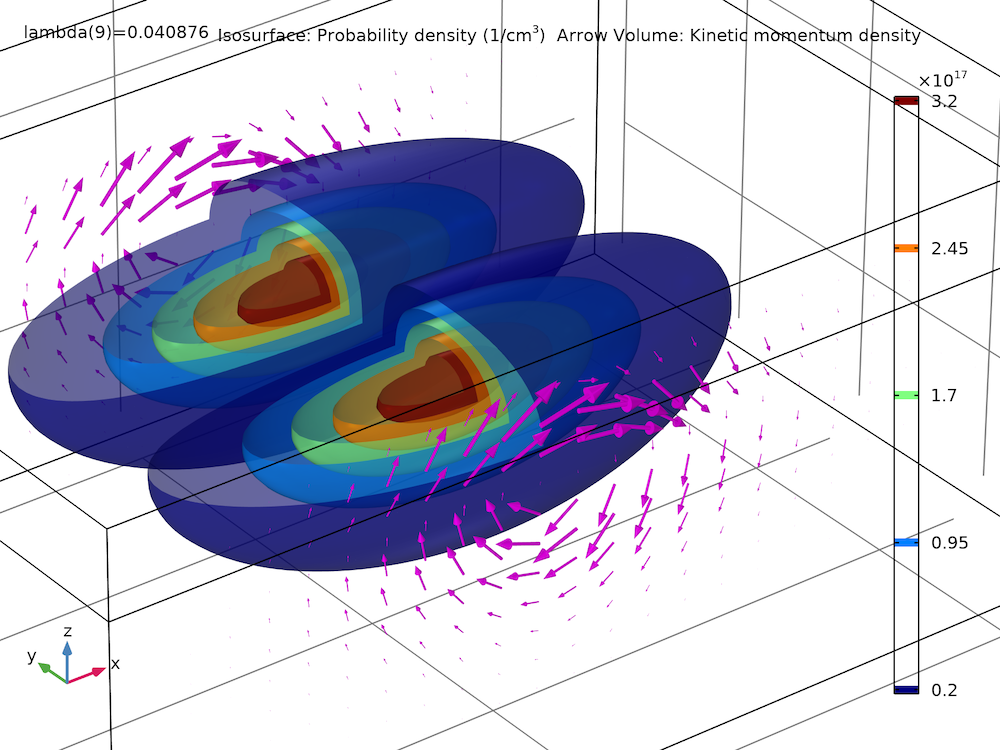
下图显示了模型缩略图的第八个激发态的概率密度(等值面)和动量密度(箭头)。使用 COMSOL Multiphysics 5.6 版本中的 透明度 子节点可以绘制透明的概率密度的等值面。
动手尝试
通过这篇博文和上一篇有关应变纤锌矿 GaN 带结构的 k•p 方法的文章,我们讨论了多分量波函数的 薛定谔方程 物理场接口的功能。您也可以自己动手尝试使用这些功能进行建模。
单击下面的按钮,尝试在均匀的磁场中对硅量子点建模,您可以点击下载 MPH 文件。
参考文献
- R.M. Jock et al., “A silicon metal-oxide-semiconductor electron spin-orbit qubit,” Nature Communications, 9:1768, 2018.






评论 (0)