计算流体力学 (CFD) 博客文章
借助 CFD 建模防止空气感染
医疗相关感染 (HAI, Healthcare-associated infections) 正影响着全球数百万人。HAI 最常见的原因是和源头直接接触，另外空气中传播的细菌也可能造成感染。为预防空气感染，让医院的洁净室更加安全放心，设计出有效的通风系统便是一个重点。有效的通风设计还能降低能耗，节约成本，带来额外收益。卓越设计的第一步是 CFD 建模。
模拟板球运动中的旋转式投球
板球是世界上第二受欢迎的运动，但人们也把它看作一项艺术。除了击球手用于保护他们的三柱门并得分的各项技能，旨在将击球手淘汰出局的各种投球方法更是综合了多种物理因素。本篇博客将分析其中的一种旋转投球技巧。
计算质量和能量守恒的方法
拟有没有想过如何计算流体流动仿真的质量守恒，或共轭传热模拟的能量平衡？如果是，请继续阅读 >>
模拟流体减震器中的粘性耗散热
流体减震器有着广泛的应用，从稳固摩天大楼到控制微流体装置中流体的流动均有涉及。通过一个称为粘性耗散热的过程，减震器将机械能消散为热能。热量过多会损坏减震器，因此在优化流体减震器的设计时，充分理解粘性耗散热的过程非常重要。
创建可用于优化搅拌器设计的 App 简介
COMSOL Multiphysics® 软件 5.0 版本为用户带来了仿真 App 创建功能，用户可以选择从零开始创建，或者基于“案例库”的演示 App 进行创建。今天，我们将介绍一款可用于分析与优化搅拌器设计，及其针对特定流体的操作状况的 App 。示例 App 对搅拌釜式反应器进行了建模与仿真，这种装置常用于精细化工、制药、食品和消费品行业的反应器。
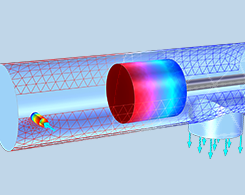
模拟硅基片上的 UHV/CVD 及硅生长
化学气相沉积 (CVD) 能够生产出兼具高质量、高纯度及高强度等优点的材料，因此在半导体行业非常受欢迎。超高真空化学气相沉积 (UHV/CVD) 涉及相当复杂的设备和极高的温度。为了能在提高效率的同时更好地控制成本，工程师们可以对这一复杂工艺进行模拟。本篇博客中，我们将以硅基片的生长为例进行说明。
如何计算升力和阻力？
在流体流动仿真中，评估流体作用在固体上的力通常很重要，例如作用在汽车或机翼上的升力和阻力。通过计算这些体力，工程师可以量化设计的效率和空气动力学性能。今天，我们将讨论在 COMSOL Multiphysics 中计算升力和阻力的不同方法。
热式质量流量传感器的行为描述
经过多年的发展，传感器技术现在能够更精确地测量流体流动行为。热式质量流量传感器就是这样一类设备。该仪器设计简单、操作方便，而且精度极高，因此很受人们的重视。剑桥大学的研究团队使用 COMSOL Multiphysics 设计了一款热流量传感器三维模型，用于分析这一流动仪零部件中的动力学。