计算流体力学 (CFD) 博客文章
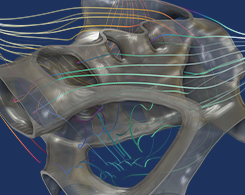
换热器的优化
2025年 6月 25日
由于换热器的设计和制造成本高昂,开发换热器是一项艰巨的任务。探索如何使用形状优化和拓扑优化来提供帮助。

非牛顿流体在多孔介质中的流动仿真
2025年 3月 27日
学习如何使用仿真开发一种均质化方法,用于模拟多孔结构中的非牛顿流。

直拉法晶体生长炉的热分析
2025年 3月 12日
Czochralski 方法是制备单晶硅晶锭的最常用方法。阅读文章,了解该方法的历史以及模拟方法。

使用 CFD 模拟赛车运动中的可调式尾翼系统
2024年 11月 26日
探索如何建立一个类似于赛车中使用的可调式尾翼系统(DRS)的襟翼简单模型。

2024 年欧洲杯官方比赛用球的空气动力学仿真
2024年 6月 14日
探索 2024 年欧洲杯官方比赛用球的复杂设计,了解它与 2018 年FIFA世界杯® 比赛用球的不同。

使用 RANS 湍流模型检测空气过滤器
2024年 2月 20日
建模和仿真可以用来分析和更好地理解各种系统中的湍流。请看这篇博客中展示的一个例子。
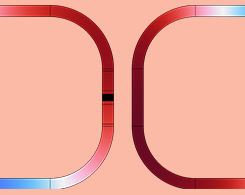
模拟热声发动机中的声能产生
2024年 2月 15日
热声发动机没有含活动部件,因此其结构非常简单。阅读这篇博客,了解更多关于热声发动机以及如何对其进行建模的信息。
通过仿真指导 mRNA 疫苗生产
2023年 8月 10日
近年来,脂质纳米粒子因其在 mRNA 疫苗生产中的应用而备受公众关注。了解 Veryst 工程公司如何利用仿真来帮助指导这一过程。
