通用 博客文章

使用自适应网格划分进行局部解的改进
选择网格对于解决方案的准确性很重要。 在这里,我们介绍了一种自适应网格划分技术,以基于局部度量细化网格。

学习高效地求解多物理场问题
我们总是被问到该如何更有效率地学习求解多物理场问题。过去的几周,我一直在撰写阐述 COMSOL Multiphysics 核心功能系列博客。这些博客旨在帮助您理解有关高效开发精确的多物理场模型背后的关键理念。今天,我将整体回顾一下该系列博文。

提高多物理场问题的收敛性
在“求解多物理场问题”这篇博客中,我们介绍了 COMSOL 中用于求解稳态多物理场问题的全耦合和分离算法。这里,我们再来看一下能够加快这两种方法收敛的一些技巧。

求解多物理场问题的 2 种算法
这篇博客,我们将介绍 COMSOL Multiphysics 中求解多物理场有限元问题的两类算法。到目前为止,我们已经学习了如何进行网格划分,以及求解线性和非线性单物理场有限元问题,但是还没有考虑过同一个域内存在多个相互影响的不同物理场的问题。

非线性静态有限元问题网格剖分的注意事项
我们已在求解器系列的部分博客中讨论了求解非线性静态有限元问题、用于改善非线性问题收敛的载荷递增,以及用于改善非线性问题收敛的非线性递增。我们还介绍了线性静态问题网格剖分的注意事项,以及在网格剖分过程中如何找到奇异性并对此进行处理。

通过递增非线性改进非线性问题的收敛
正如之前在 “非线性问题的载荷递增“博客中所讨论的,当求解一个问题时,我们可以从一个已知解的无载荷问题开始,然后使用延拓法逐渐递增载荷来进行求解。这个算法同样适用于理解接近失效的载荷时的情况。然而载荷递增并非适用于所有情况,在某些情况下可能无法发挥效用。本篇博客中,我们将介绍如何通过非线性递增改进问题的收敛。

非线性问题的载荷递增
正如我们之前在“求解非线性稳态有限元问题”博客中所看到的,并不是所有的非线性问题都可通过阻尼 Newton-Raphson 法求解。尤其是当选择了一个不合适的初始条件或者设定一个无解的问题时,只会造成非线性求解器持续执行迭代而无法收敛。在此我们介绍一种更为可靠的非线性问题解决方案。

求解非线性稳态有限元问题
本篇博客中,我们将简要介绍求解非线性稳态有限元问题的算法,并通过一个非常简单的一维有限元问题来演示这些内容,即我们在“求解线性稳态有限元模型”博客中所讨论的那个问题。

线性方程组的解:直接和迭代求解器
本篇博客中,我们将向您介绍使用 COMSOL 求解任何有限元问题时,其中所用的两类线性方程组的求解算法。这些信息与理解求解器的内部工作原理,以及内存使用如何随问题大小变化等相关。

选择合适的单元进行网格划分
在上一篇博客中,我们介绍了线性静态问题的网格划分注意事项。其中,网格收敛是一个关键概念,因为随着网格的细化,解将变得更加精确。这篇博客,我们将更加深入地探究:对于线性静态有限元问题,如何选择合适的网格进行网格收敛研究。

网格剖分时识别并解决其中的奇异性
阅读之前的一篇博客 “线性静态问题的网格剖分注意事项”,我们发现,有限元模型的解将能在网格细化的限度内收敛至真实解。不仅如此,我们还了解到,在误差较高的区域,可以通过自适应网格细化生成包含更小单元的网格,而不是简单地在整个模型内都使用较小的网格单元。

线性静态问题的网格剖分注意事项
本篇博客中,我们介绍了线性静态有限元问题的网格剖分注意事项。这是网格剖分技巧系列博客的第一篇,希望能帮您建立起对有限元模型剖分网格的信心。

求解线性稳态有限元模型
本篇博客是求解器系列的首篇博客,将介绍用于求解所有线性稳态有限元问题的算法。虽然我们在博客中基于一维有限元问题进行介绍,但所讲解的内容具有普适性,能帮助您理解博客系列中接下来将介绍的更加复杂的非线性多物理场的求解技巧。
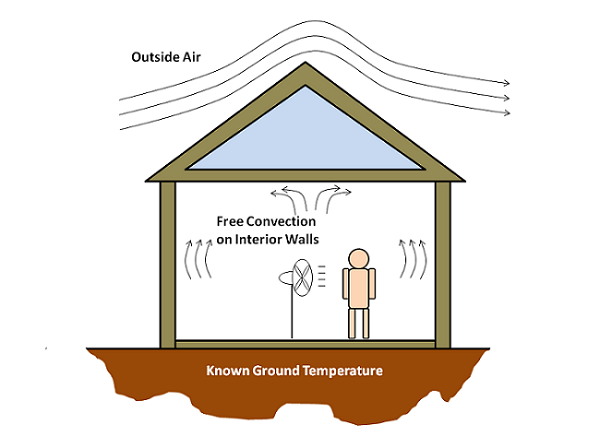
使用全局方程模拟室内空气温度
前些天我遇到了一个有趣的问题,它促发了我想要写一篇博客的灵感,因为它使我想到了我们的 COMSOL Multiphysics 软件中一个非常强大但常常没有得到充分利用的功能:全局方程。

如何执行网格细化研究
几周前,我主持了一场有关 COMSOL Multiphysics 后处理和可视化特征的网络研讨会。这场网络研讨会在 COMSOL 用户中的反响非常好,因此我特意写了本篇博客,希望再次强调下我们所涉及的一个重要专题,即在 COMSOL Multiphysics 中进行网格细化研究。
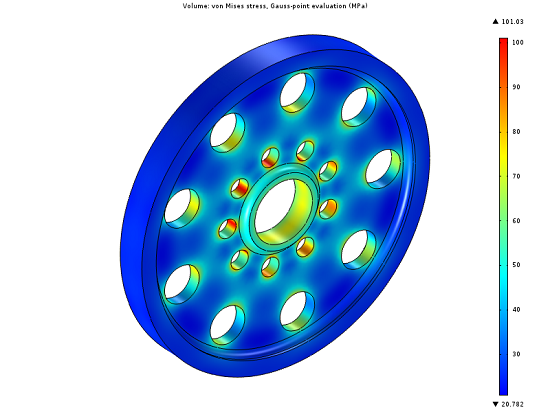
使用无梯度的优化方法求解模型
COMSOL 软件的优化模块包含基于梯度和无梯度的优化 2 种功能。基于梯度的优化方法可以计算目标函数和任何相关约束函数的精确解析导数,但它要求函数是平滑和可微分的。在这篇博客中,我们将研究无梯度优化器的使用,它可以考虑不可微分或不平滑的目标函数和约束条件。为了减轻质量,同时保持对零件峰值应力的约束,我们对旋转轮的尺寸进行了优化。 旋转轮的压力 旋转的轮子会产生离心应力,从而导致整个零件产生应力。为了减轻质量,轮毂上被切割了一些规则的孔洞。下图中显示了离心力产生的 von Mises 应力。我们希望进一步减轻质量,同时将应力保持在临界值以下。 求解应力 虽然我们可以一次对整个轮子进行建模,但由于这个零件存在镜面对称和旋转对称,因此可以减小模型,从而最大限度地降低计算要求。对称边界条件用于约束该零件。 基于旋转速度、旋转轴和材料密度施加体载荷,用于模拟离心力。该模型使用瞬态求解器求解,即假设转速恒定。 选择设计变量 在这个示例中,假设已经有了一套制造工艺,我们希望对零件的整体设计做最小的改动,以降低重新加工的成本。设计变量的一个常见选择就是改变轮毂上孔的半径。因此,我们回到几何序列,对孔的半径及其位置进行参数化。我们还可以根据纯粹的几何分析推算出,每个孔的最大半径必须有一定的限制,否则孔与孔之间的区域会变得太薄,孔与孔之间就会重叠。我们还将对最小半径设限,因为我们不希望孔洞完全消失。 定义目标函数和约束条件 这里的优化目标只是减少零件的质量,即所有域上材料密度的积分。 优化目标是使质量(密度的积分)最小。 这个约束条件稍微复杂一些;我们希望尽量减小零件的峰值应力。但是,我们并不知道峰值应力会出现在哪里。如果内孔或外孔太小,就会导致孔周围应力集中。如果我们将孔的半径做得过大,孔之间的材料就会变得过薄,同样会导致高应力。因此,我们必须监控整个零件的最大应力,并将其限制在指定的峰值应力以下。这是一种无差别约束,尤其需要使用无梯度优化方法。 峰值应力通过域探针进行监测,并命名为 PeakStress。 峰值应力变量受限于一个上限。 用无梯度优化法求解问题 为了求解优化问题,我们在研究分支下添加了优化 功能。Nelder-Mead 方法是两种无梯度方法之一(另一种是坐标搜索)。无梯度优化算法还允许当几何尺寸变化时重新划分网格。 目标函数和约束条件由模型树中的优化 分支定义。控制变量给定了初始条件,我们指定了上限和下限。优化后的设计有很大不同——质量减少了 20%,同时保持了对峰值应力的限制。
曲线坐标的用法
曲线坐标是一种坐标线可以弯曲的坐标系。COMSOL 4.3b 版本软件中新增了自动计算曲线坐标的用户接口,对于那些在自由曲面 CAD 设计中处理各向异性材料的用户来说,这是一个非常实用的补充。

石墨烯革命:第五部分
在一篇名为”选择石墨烯基晶体管的栅介质“的论文中,讨论了半导体形式石墨烯的应用。正如我们之前所了解的,单层石墨烯并非一种半导体,它是一种零带隙导体(半金属)。人们正尝试向石墨烯中引入带隙,这将使它变得半导电,室温迁移率将比硅高一个数量级。人们现在正积极思考在攻克剩余技术难题之后,如何应用这类材料。半导体石墨烯的应用之一是设计下一代快速切换金属氧化物半导体场效应晶体管(MOSFET)。

石墨烯革命:第四部分
石墨烯可以在高真空下利用热分解制造。为了设计和优化这些高真空系统,工程师可能转向仿真寻求帮助,不过目前还没有多少仿真工具能胜任这一工作。让我们来看一下真空系统如何与石墨烯的生产相关,为什么要模拟它们,以及如何模拟。

石墨烯革命:第二部分
我在之前的一篇博客中曾经介绍过石墨烯的一些奇异特性。石墨烯仅包含单层原子,这意味着任何石墨烯基结构都将有极高的纵横比;而高纵横比的几何也为模拟带来了各种挑战。 石墨烯的传热模拟 COMSOL 提供了多种工具来帮助模拟具有极高纵横比的几何及特征。最近,人们利用 COMSOL 对石墨烯“被子”进行了传热模拟,《Nature Communications》杂志的”用于高功率 GaN 晶体管热管理的石墨烯被子“一文介绍了该研究。论文作者使用 COMSOL Multiphysics 证实,可通过引入由薄层石墨烯 (FLG) 制作的额外散热通道,即顶面导热片,来显著提升 AlGaN/GaN 异质结场效应晶体管 (HFET) 的局部热管理。 COMSOL Multiphysics 的传热接口支持您使用薄层特征特征模拟极高纵横比的组件。这一特征仅求解表面切面处的传热方程,因此免去了在高纵横比层中使用极端细化网络的需求。使用此方法能够极大减少计算时间和内存使用。 薄层特征设定窗口。 石墨烯的电气模拟 从 2006 年开始,人们就已经使用 COMSOL 来研究石墨烯的电气特征。在这篇论文中,研究人员使用 COMSOL 来推导石墨烯基复合材料的面内和横向电导率。我们可以很轻松地在 COMSOL Multiphysics 中输入电导率的张量物理量。您仅需提供电导率张量元,它可以是温度或其他任何量的函数。 可以轻松在电流接口电流守恒特征的设定窗口中指定各向异性电导率。 石墨烯的结构力学模拟 COMSOL 也可以模拟石墨烯的结构力学应用。在这篇论文中,研究人员计算了石墨烯膜在压力差作用下产生的挠度和应变。可通过电气检测到带结构中的变化,这说明它可用于制造超灵敏压力传感器。结构力学模块的壳接口主要用于薄壁结构中的结构力学分析,因此非常适合此类应用。壳接口使用 Mindlin-Reissner 类公式,即考虑了横向剪切形变。这意味着我们无须对极薄结构进行网格剖分,就可以获得高精度的结果。 壳接口中材料模型的设定窗口。 相关示例模型 我们现在已经分析了热学、电气以及力学的模拟概念,您可能在想有什么模型能同时用到所有这些概念。确实有一个,您可以查看案例库中电路板加热模型,如下所示。 电路板加热模型演示了热学、电气以及力学模拟概念。 这一多物理场示例模拟了加热电路器件时电热的产生、传热,以及机械应力和变形。模型用到了传热模块的固体传热接口,AC/DC 模块的电流,壳接口,以及结构力学模块的固体力学和壳接口。

在 COMSOL 模型中使用点云数据
有的时候,我们需要将其他仿真工具中的数据导入到 COMSOL Multiphysics 模型中。有很多种方法可以做到这一点,但最简单的方法是通过一个电子表格格式的文本文件读取点云数据。
