通用 博客文章

空间与时间的积分方法概述
积分是数学模型中最重要的功能之一,特别是对数值仿真而言。例如,偏微分方程组 (PDEs) 就是由积分平衡方程派生而来。当需要对偏微分方程进行数值求解时,积分也将发挥非常重要的作用。本篇博客介绍了 COMSOL 软件中可用的积分方法,以及如何使用,供您参考。
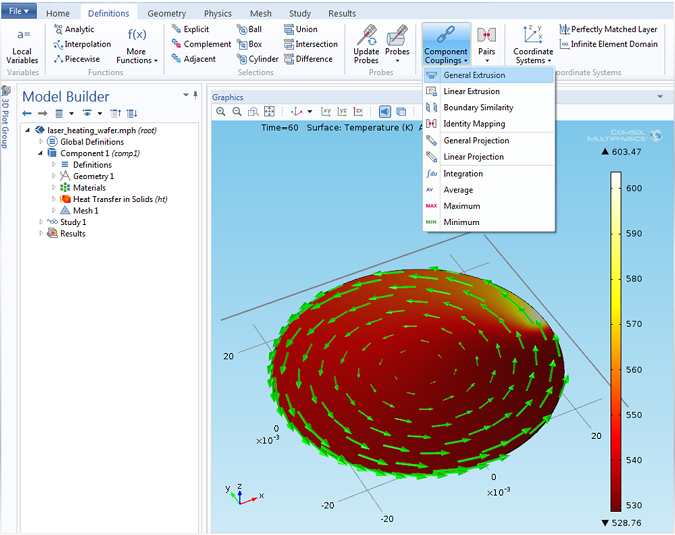
在 COMSOL 中使用广义拉伸耦合算子:动态探测
请看一个激光加热的例子,热源(激光)在移动,几何体也在移动。如何使用广义拉伸耦合算子在几何体的某一点上探测解?

利用混合并行计算技术加速物理场仿真
二十年前,配备了多达 1000 个处理单元的向量处理器超级计算机在超级计算机 500 强中占据了统治地位。随着时间推移,大规模并行计算集群不仅迅速取代了向量超级计算机成为了榜单中的新霸主,同时还促使了分布式计算的兴起。集群的每个计算节点上最初只有一个专用于高性能计算的单核处理器,很快,人们针对需要共享内存的节点,增加节点上的处理器数量,并以这种具备内存共享能力的并行计算机为基础,开发出了多核处理器,满足了各类计算应用对高效算法的需求。再看今天的超级计算机 500 强排名,我们会发现当中大多数集群均由数量众多的计算节点组成,每个节点又包含多个插槽(socket),每个插槽连接着最多可达八核的多核处理器。并行计算是一种适用于共享内存计算系统的技术,与基于分布式内存的集群采用的并行计算技术全然不同。为了实现高效率的并行计算,我们需要一种两者并用(混合)的机制。
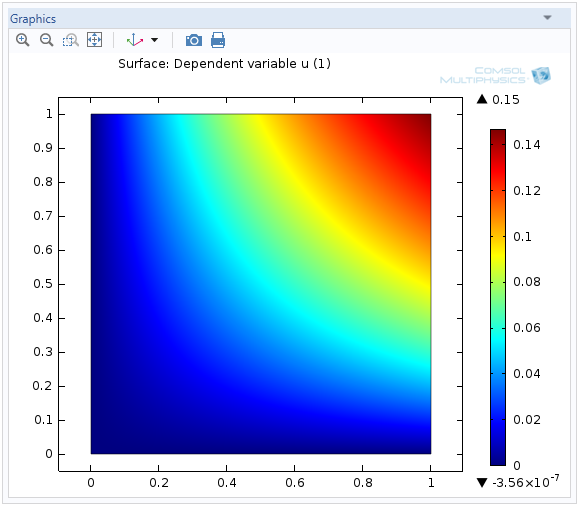
求解代数场方程
COMSOL Multiphysics® 通常用于求解 PDE,ODE 和初始值问题。但是,您是否知道它也可求以解决代数方程,甚至超越方程?
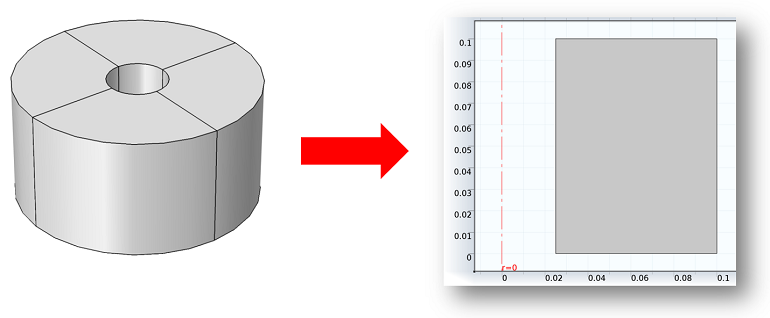
由二维轴对称电磁模型创建可视化三维绘图
今天,我们将介绍在 COMSOL 软件中如何绘制矢量场的三维视图,这些矢量场由 RF 模块和波动光学模块中的电磁波、频域 接口的二维轴对称公式计算获得。 由二维轴对称解生成三维绘图 回想一下,COMSOL 软件中的时谐分析 假设场分量根据 e^{j\omega t} 在时间上振荡,其中 \omega 是角频率。在二维轴对称公式中,电场的角度依赖性由 e^{-j m \phi} 计算,其中 m 是用户指定的整数。由时间和角度的相关性 e^{j(\omega t-m \phi)},可知电场围绕 Z 轴 旋转。我们的目标是由具有这种角度依赖性的二维轴对称解创建三维绘图。 使用二维旋转数据集创建三维绘图 在计算出二维轴对称问题的解之后,COMSOL Multiphysics 会自动生成一个名为“二维旋转”的位于“数据集”节点下的二维数据集,如下图所示。 旋转数据集可用于绘制三维视图。由于我们绘制的是三维绘图,因此将完成一次从 0° 到 360° 的完整旋转。“二维旋转1”的设置如下所示。可以看到,在 “旋转层”下,起始角度被设置为 0,旋转角度被设置为 360。 二维轴对称计算中的平面坐标为 (r,z)。由于角度 \phi 不属于计算域,因此没有被定义。不过,可以通过选中“定义变量”旁的复选框将它添加为三维数据集中的坐标。“二维旋转1”数据集中的角度变量名被设置为“rev1phi”,并可用于下文中的绘图和导出值的表达式中。 如下图所示,考虑一个带矩形截面的轴对称谐振腔。在二维轴对称公式中仅模拟矩形截面。 我们可以使用特征频率研究计算谐振模式。假设我们想绘制 m = 1 模式的场量。下图左侧为在 rz 平面 绘制出的电场大小。我们还可以在将空腔一分为二的表面上绘制电场的大小,这是使用 xy 平面 上的“emw.normE”三维切面图绘制的,平面数被设为 1。右下图中绘制了电场的大小。由于场是围绕 Z 轴 旋转的行波,因此它是轴对称的,这也是因为它遵循 | e^{j(\omega t – m \phi)} | = 1。 绘制电场的径向分量 现在,我们来绘制空腔平面内电场径向分量的实部。具体来说,我们将绘制 t=0 时的 Re { E_r(r,z) \, e^{j(\omega t-m \phi)} },其中 […]

使用自适应网格划分进行局部解的改进
选择网格对于解决方案的准确性很重要。 在这里,我们介绍了一种自适应网格划分技术,以基于局部度量细化网格。

学习高效地求解多物理场问题
我们总是被问到该如何更有效率地学习求解多物理场问题。过去的几周,我一直在撰写阐述 COMSOL Multiphysics 核心功能系列博客。这些博客旨在帮助您理解有关高效开发精确的多物理场模型背后的关键理念。今天,我将整体回顾一下该系列博文。

提高多物理场问题的收敛性
在“求解多物理场问题”这篇博客中,我们介绍了 COMSOL 中用于求解稳态多物理场问题的全耦合和分离算法。这里,我们再来看一下能够加快这两种方法收敛的一些技巧。



