
毫不夸张的说,约翰·斯科特·罗素 (John Scott Russell) 的一生都对追求科学充满热情。当年,他在观察马拉着一艘船穿过一条浅运河时,注意到一个奇怪的波,并骑着马跟着它走了一两英里。在他的余生中,他不停地在“追逐”这股波浪(他称之为“移动波”),即使他的理论受到了当时一些科学家的嘲笑,他也坚持不懈的研究。那么,罗素”追”上他的波了吗?
一匹马、一艘快艇和一位好奇的海军建筑师
如果你生活在 19 世纪 30 年代的格拉斯哥(Glasgow),游览苏格兰的最好方式之一就是在格拉斯哥、佩斯利(Paisley)和阿尔德罗山(Ardrossan)运河上乘坐马拉的飞艇。那些飞艇又轻又长又窄,被马拉着穿过运河的浅水区。


苏格兰格拉斯哥的现代景观(左)和苏格兰中部的一条运河,这里是被称为法尔柯克轮(Falkirk Wheel)的旋转船升降机的所在地(右)。
一天,一家快艇公司的老板威廉·休斯顿(William Houston)正乘坐快艇沿着一条运河航行,突然,拉着快艇的马被吓了一跳,拔腿就跑。休斯顿注意到一些奇怪的事情:水没有表现出阻力。这艘船滑行得很快(类似于我们现在所说的“水上滑行”),船只运动产生的湍流没有损坏运河的沿岸(参考文献1)。
罗素是格拉斯哥的一名造船工程师。当他听说休斯顿观察到的现象时,他认为亲眼目睹这个过程可以让他对船只设计有所了解。他在观察运河时,其中一匹马突然停下来。这时,在船的中间形成一个波浪,并移动到船头,然后完全离开船前行。罗素紧随其后,先是步行,然后骑马。他惊讶地看到这些波以相同的大小和速度继续前进。他后来把它称为“移动波”,并将这一经历描述为“我一生中最快乐的一天”。(参考文献2)

1847 年的约翰·斯科特·罗素。在美国公共领域的形象,来自维基共享空间。
罗素花了两年时间在实验室复制移动波,因为这样他就可以进一步研究它。他建造了一个 30 英尺的水池来测试他的新理论。最终,他观察到了这些波的一些独特性质,现在被称为孤波。根据罗素的说法,孤波具有以下特点:
- 以稳定的方式长距离行驶
- 移动速度取决于其大小
- 宽度取决于水的深度
- 不与其他波结合(相反,大波浪会超过小波浪)
- 如果相对于水深来说太大,则会分裂成两个不同大小的波浪
显示孤波行为的动画。
他还将这些波分为四种类型:
- 平移波,涉及质量传递,要么是孤波,要么是一系列次级波
- 振荡波,一组连续波组(如风产生的波)
- 毛细波,由非常小的水的搅动引起,取决于表面张力
- 微粒波,快速连续的孤波(如声波)
罗素在爱丁堡举行的英国科学协会会议上介绍了他的发现,描述了孤波及其背后的力学原理。他的工作包含对力学定律基础的一些误解——这是可以理解的,因为他的背景是建筑,而不是物理。当时的科学家对他的理论半信半疑,怀疑他缺乏工程和物理专业知识的理论。
就这样,罗素开始了一生(实际上时间更长)对孤波行为的研究。
对孤波的初始反应
起初,罗素的孤波理论在科学界没有赢得多少粉丝。研究波与潮汐关系的乔治·比德尔·艾里(George Biddell Airy)并不十分重视罗素的理论,他认为孤波与皮埃尔·西蒙·拉普拉斯(Pierre-Simon Laplace)的流体力学理论是矛盾的。正如我们所知道的,拉普拉斯方程是当今流体动力学研究的组成部分(参考文献1)。
著名的纳维尔-斯托克斯方程的作者乔治.斯托克斯(George Gabriel Stokes) 也不支持孤波的可能性,最初他质疑它们与潮汐和声波的关系。随着时间的推移,当他研究有限振荡波时,他改变了立场,承认理论上的孤波是合理的(参考文献1)。
与此同时:重回造船业
罗素从未放弃孤波这个话题,但他仍继续从事着他的主要工作:造船。他利用对波的研究设计了一种特殊的船艏,这种船艏是基于我们熟悉的正弦波的形状建造的,可以更好地处理水阻力。
19 世纪 50 年代, 伊桑巴德·金德姆·布鲁内尔(Isambard Kingdom Brunel)请求罗素帮助他建造一艘名为“大东方号”(Great Eastern)的轮船。“大东方号”由布鲁内尔设计,被认为是当时最大的船(他亲切地称它为“伟大的宝贝”)。据说这艘船可以从英国航行到澳大利亚,不需要加油。

首次航行前的大东方。在美国公共领域的形象,通过维基共享空间。
罗素采纳了布鲁内尔的设计,成功建造了“大东方号”。这艘船最终完成了多次跨大西洋的航行。然而,布鲁内尔在船航行前不久就去世了,并且船在它的处女航中发生了一次重大事故,他的设计受到了质疑。大约在这个时候,罗素的财务也出现了问题,他的资产被没收。
潮汐是如何变化的: 布辛涅斯克和 KdV 方程
在他生命的最后阶段,罗素的孤波仍然受到科学家的指责,他破产了。幸运的是,事情即将发生转机。
约瑟夫·瓦伦丁·布辛涅斯克(Joseph Valentin Boussinesq)是圣维南(Adhémar Jean Claude Barré de Saint-Venant)的门徒,以在流体动力学领域的贡献而闻名,他并没有像当时的其他人一样忽略罗素的理论。相反,他对波和潮汐的各个方面都进行了数学分析。1872年,布辛涅斯克试图解释浅水波,因此推导了一个方程,以证明孤波在理论上是可能的。他甚至在1877年的论文中提到了罗素。瑞利勋爵(Lord Rayleigh)也独立提出了类似的波理论,支持罗素的发现(参考文献 1)。
最后,两位科学家呼吁大家支持罗素的发现!1882年,74岁的罗素在英国怀特岛去世。但故事并没有就此结束。
1895 年, 科特韦格(Diederik Korteweg)和德弗里斯(Gustav de Vries)对布辛涅斯克的工作进行了扩展,并发展了一个方程,证明孤波在理论上是可能的。KdV方程没有引入耗散,这意味着可以用它来描述长距离传播的波,同时保持它们的形状和速度。该方程也比布辛涅斯克方程简单,并给出了更优的解(参考文献2)。由于这些优点,KdV 方程至今仍被用来理解各种形式的波的行为。
孤波的现代研究
对孤波的研究始于 1965 年,当时研究人员 Diederik Korteweg 和 Gustav de Vries 更详细地研究了 KdV 方程。他们发现孤波不仅可以在理论上出现,而且可以自然出现,并创造了“孤子(solitons)”一词来描述它们。此外,随着对光学、声学和其他领域应用的研究,孤子不再仅仅被认为是仅在水波中存在。
1967 年, Krustal 与研究人员 Gardner、Greene 和 Miura 一起开发了逆散射变换法。这种方法可以用来寻找KdV方程的精确解,也证明了最初由 Krustal 和 Zabusky 观察到的波之间的弹性碰撞。(参考文献2)

水中的孤子。图像来自 Christophe。Finot et Kamal HAMMANI。根据 CC BY-SA 2.5许可,通过Wikimedia Commons 共享。
同样,科学家 Zabusky 和 Shabat 使用 Peter Lax 开发的公式求解非线性薛定谔方程,该方程描述了一般波包的缓慢包络的演化。Ablowitz、Kaup、Newell 和 Segur 后来提出了一种更系统的方法来求解非线性薛定谔方程,现在被称为 AKNS 方法。(参考文献2)
所有这些围绕孤子的数学活动吸引了科学界的注意,而这是罗素无法做到的。在接下来的 30 年里,孤子在不同领域得到了广泛的研究,包括地质力学、海洋学、天体物理学和量子力学等等。
光纤中的孤子
光纤是孤子的一个重要的实际应用领域。光纤的线性色散特性使孤子达到平衡,而其非线性特性有助于孤子达到聚焦效果。结果是一个非常稳定的脉冲,似乎可以永远传播一样。
这种行为最初是由贝尔实验室的一个研究团队在 20 世纪 80 年代观察到的,该团队由 Linn Mollenauer 领导,目的是将孤子应用于远程通信系统。在 20 世纪 90 年代,麻省理工学院的一组研究人员在传输系统中添加了滤光器,试图最大化光孤子的传播距离。利用这种方法,Mollenauer 的团队发送了一个超过 20000 公里的 10Gbit/s 的信号——这在当时是令人印象深刻的(参考文献2)。21 世纪,光孤子研究进入了矢量孤子领域,矢量孤子有两个不同的偏振分量。
Lahav 等人目前的研究旨在创造在所有三维空间都稳定的孤子,称为“轻子弹”。这需要同时消除衍射和色散,这在高度结构化的材料中已经实现,而在可用于实际应用的非结构化材料中却没有实现。Lahav 团队研究了 3D 孤子的基本特性,以开发光纤中孤子的更多技术应用。他们还开发了一种方法,包括将一串重复的光脉冲照射到一种称为“铌酸锶钡”的特殊材料中,以产生自导向光束并抵消色散。这种方法产生了一串 3D 孤子,有可能用于先进的非线性光学和光学信息处理(参考文献3)。
基于方程的建模支持“即开即用”的孤子分析
KdV 方程的解告诉我们,孤子的速度决定了它的振幅和宽度。通过研究这种效应,我们可以更好地预测光应用中孤子的行为和局限性。通过仿真可以可视化孤子的行为,而无需建立资源耗费或昂贵的光学实验。除了演示速度如何影响波的振幅和宽度,仿真还显示了孤子如何碰撞和再现,同时保持它们的形状(就像罗素观察到在海洋中“超越”对方的孤波)。
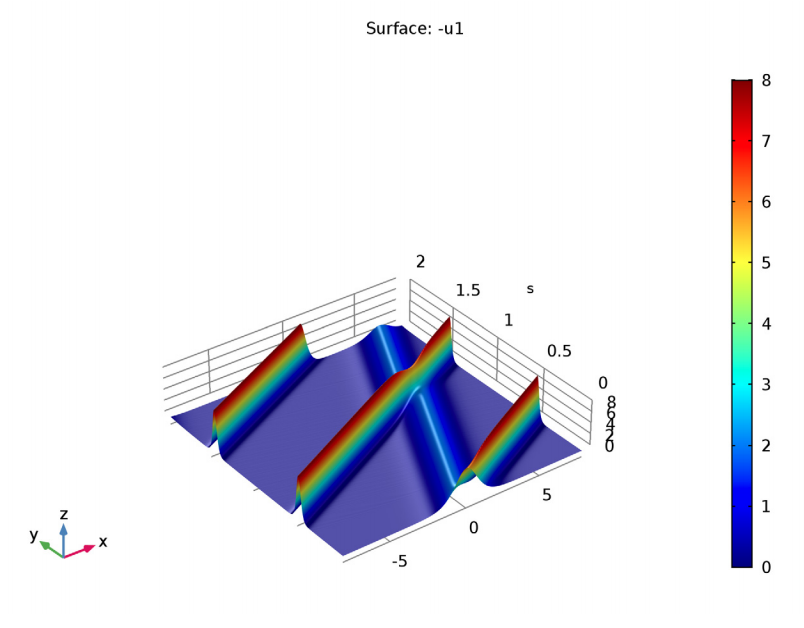
仿真结果显示了孤子碰撞和再现。图像来自 COMSOL KdV 方程和孤子教程模型。
预定义的物理设置对于简单的建模任务来说是一个有效且简单的选项;然而,这对于光孤子行不通。基于方程的建模使我们能够对需要灵活性和创造性的问题进行建模,以扩展可能的内容。使用基于方程的建模,添加偏微分方程 (PDE) 和常微分方程 (ODE)将 KdV 方程无缝地应用到COMSOL Multiphysics® 软件中。我们甚至可以从自定义设置中创建一个物理接口,这样就不必在下次需要建立模型时从头开始。
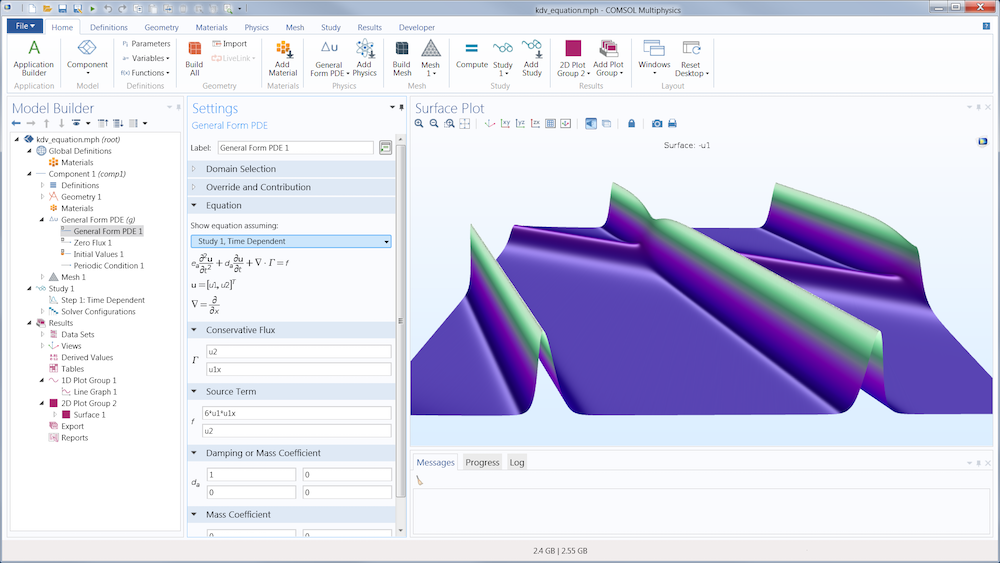
在 COMSOL Multiphysics 图形用户界面(GUI)中向孤子模型添加偏微分方程。基于方程的建模示例。
基于方程的建模功能使得模拟光纤中的初始脉冲以及由此产生的波或孤子成为可能。
总结性思考
1885 年,罗素的著作 The Wave of Translation in the Oceans of Water, Air and Ether 在他去世后出版。其中包括他对物质物理学的推测,以及如何分别通过计算声速和光速来找到大气和宇宙的深度(参考文献4)。甚至在他生命的最后,罗素仍继续从理论上阐述我们如何将数学应用到可观察的世界,以及孤子在现代物理中的意义。要是他能亲眼看到 KdV 方程的发展或光学的最新进展就好了。
罗素的支持者之一,Osborne Reynolds,在他自己对孤波的研究中做了一个恰当的观察:在深水中,成组的波的传播速度比形成它们的单个波要快(参考文献1)。也许我们可以把罗素看作是激励他人朝着共同目标不断前进的个人浪潮。
下一步
单击下面的按钮,了解更多关于基于方程的建模以及 COMSOL Multiphysics 中的其他特性和功能。
参考文献
- O. Darrigol, “The Spirited Horse, the Engineer, and the Mathematician: Water Waves in Nineteenth-Century Hydrodynamics,” Archive for History of Exact Sciences, vol. 58, pp. 21–95, 2003.
- B. Kath and B. Kath, “Making Waves: Solitons and Their Optical Applications,” SIAM News, vol. 31, no. 2, pp. 1–5, 1998.
- F.W. Wise, “Solitons divide and conquer,” Nature, vol. 554, pp. 179–180, 2018.
- Topics in Current Physics: Solitons, R.K. Bullough and P.J. Caudrey, eds., Springer-Verlag, pp. 373–379, 1980.






评论 (0)