
电子能量分布函数(EEDF)在等离子体建模中起着重要作用。我们可以使用多种方法来描述电子能量分布函数,例如使用像麦克斯韦或 Druyvesteyn 函数这样的分析函数,或者求解玻尔兹曼方程。今天,我们将介绍不同的电子能量分布函数对等离子体模拟结果的影响。
编者注:本博文于 2022 年 3 月 4 日更新,以反映 COMSOL Multiphysics® 软件 6.0 版本的新功能。
电子能量分布函数
电子能量分布函数在等离子体建模中至关重要,因为需要用它通过合适的电子碰撞截面计算电子源项和传递参数。在 COMSOL 软件中,默认情况下,等离子体 接口使用的是麦克斯韦电子能量分布函数。这是一个很好的建模起步,可以建立一个准备模型并获得一般的分布趋势(例如,电子密度与施加的电压)。然而,对于更详细的研究,应该使用预先计算的电子能量分布函数,因为对于大多数冷的等离子体应用,电子能量分布函数处于强烈的非平衡状态。换句话说,电子能量分布函数在很大程度上偏离了麦克斯韦分布。在下面的章节中,我们介绍了用于分析电子能量分布函数及其对介质阻挡放电反应器模拟结果的影响的几种方法。
描述电子能量分布函数
为了描述电子能量分布函数,COMSOL 提供了有几种可能的方法,如麦克斯韦 或Druyvesteyn 函数。此外,还有一种广义的形式,是介于麦克斯韦和 Druyvesteyn 函数之间的函数。
用于描述电子能量分布的函数
| 麦克斯韦函数 |
f(\epsilon)=\varphi^{-3/2}\beta_1\exp\left(-\frac{\epsilon\beta_2}{\varphi}\right)
\beta_1=\Gamma(5/2)^{3/2}\Gamma(3/2)^{-5/2},\ \beta_2=\Gamma(5/2)\Gamma(3/2)^{-1}
|
| Druyvesteyn 函数 |
f(\epsilon)=\varphi^{-3/2}\beta_1\exp\left(-\left(\frac{\epsilon\beta_2}{\varphi}\right)^2\right)
\beta_1=\Gamma(5/4)^{3/2}\Gamma(3/4)^{-5/2},\ \beta_2=\Gamma(5/4)\Gamma(3/4)^{-1}
|
| 广义函数 |
f(\epsilon)=\varphi^{-3/2}\beta_1\exp\left(-\left(\frac{\epsilon\beta_2}{\varphi}\right)^g\right)
\beta_1=\Gamma(5/2g)^{3/2}\Gamma(3/2g)^{-5/2},\ \beta_2=\Gamma(5/2g)\Gamma(3/2g)^{-1}
|
这里, ϵ 是电子能量 (eV);\varphi 是平均电子能量(eV);g 是介于 1 和 2 之间的系数。
对于麦克斯韦分布函数,g 等于 1;对于Druyvesteyn 函数,g 等于2;\Gamma 是不完全 Gamma 函数。
分布函数假定弹性碰撞占主导地位,因此非弹性碰撞(如激发或电离)对分布函数的影响不明显。在这种情况下,分布函数呈球形对称。在与中性原子的弹性碰撞中,电子的运动方向会发生改变,但不会改变其能量(由于质量差异较大)。
麦克斯韦函数
如果电子处于热力学平衡状态,则分布函数为麦克斯韦方程。然而,这只在电离度高的情况下才成立。电离度高时,电子与电子的碰撞推动能量分布转向麦克斯韦函数形状。下图显示了两种不同形式的麦克斯韦电子能量分布函数。
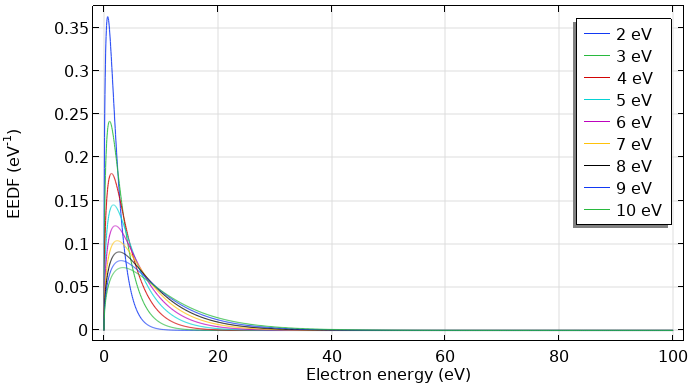
平均电子能量为 2–10 eV 的麦克斯韦电子能量分布函数(eV-1)。
通常,分布函数是以 \sqrt{\epsilon} 划分的。这种分布函数也称为电子能量概率函数(EEPF)。对于麦克斯韦函数,电子能量分布函数为一条斜率为 (-1/k_B T) 的直线,如下图所示。
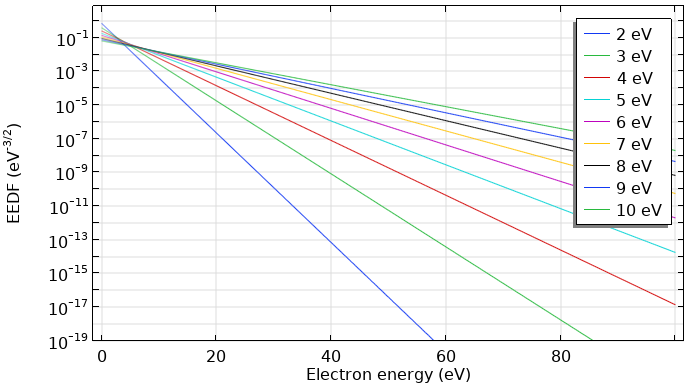
平均电子能量为 2–10 eV 的麦克斯韦电子能量分布函数(eV-3/2)。
Druyvesteyn 函数
与麦克斯韦电子能量分布函数不同,Druyvesteyn 电子能量分布函数假设了一个恒定的、与电子能量无关的横截面。这导致对于相同的平均电子能量,在较高的电子能量下,电子能量分布函数会下降。
玻尔兹曼方程
此外,还可以通过求解玻尔兹曼方程来计算电子能量分布函数。玻尔兹曼方程描述了分布函数 f 在六维相空间中的演化:
{\partial f} {\partial t}
+\mathbf
{v}\cdot\triangledown f-\frac{e}{m}(\mathbf{E}\cdot\triangledown_\mathbf{v}
f)=C[f]
为了在合理的时间内求解电子的玻尔兹曼方程,进而计算电子能量分布函数,有必要对方程进行大幅简化。一种常用的方法是在球谐函数中展开分布函数。假设电子能量分布函数几乎是球对称的,因此可以删除第二项之后的级数 (所谓的两项近似)。COMSOL 软件的 玻尔兹曼方程、两项近似 接口就使用了这个方法。
从上述介绍的分布函数来看,由于引入了各向异性扰动,玻尔兹曼方程,两项近似法是计算电子能量分布函数最准确的方法。使该方法更精确的另一个原因是,通常能量分布函数是基于提供的电子碰撞截面的相干集来计算的,这些截面描述了电子在与背景气体碰撞时如何失去/获得能量。电子通过这种方式,能量分布函数描述了电子如何从电场中获得能量,并在特定气体或气体混合物的碰撞中失去能量。
麦克斯韦、Druyvesteyn 函数与计算的分布函数的比较
如下图所示,计算的电子能量分布函数明显偏离麦克斯韦电子能量分布函数。主要的区别是,当电子达到氩的第一电子激发态能量 11.5 eV 时,高能端明显下降。计算的能量分布函数在低能时密度不足,而在中能时密度过高,在第一个激发能级之前的区域斜率变化缓慢。这种电子能量分布函数通常是在惰性气体的低温等离子体中获得的。
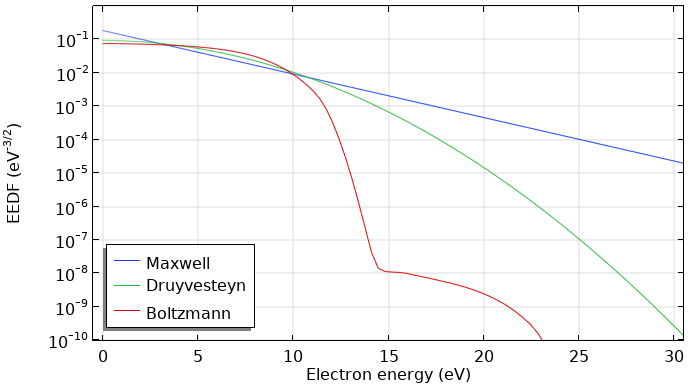
比较使用麦克斯韦, Druyvesteyn 函数和 玻尔兹曼方程,两项近似 接口计算的氩能量分布函数。所有能量分布函数的平均电子能量为 5 eV。
速率系数和传递参数
在等离子体模型中,需要通过以下公式使用电子能量分布函数计算电子碰撞反应的速率系数k_k :
\epsilon\sigma_k(\epsilon)f(\epsilon)\mathrm d\epsilon
上式中, \gamma = \sqrt{2q/m_e}, ϵ 是电子能量, \sigma_k 反应 k 的截面。
激发和电离的速率系数高度依赖于能量分布函数的形状。这主要是由于在能量超过第一激发能级阈值时,电子聚群会迅速下降。使用麦克斯韦能量分布函数会高估电离率,如下图所示。
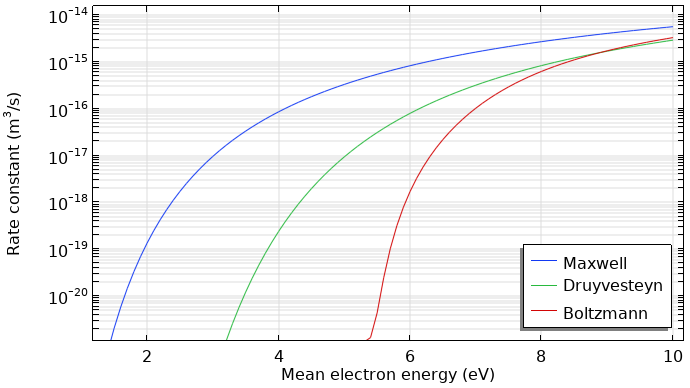
用不同类型的电子能量分布函数计算的氩离子电离速率系数。
此外,利用 玻耳兹曼方程,两项近似 接口,可以利用电子能量分布函数计算电子的传输属性。计算得到的传递系数对能量分布函数类型的依赖性较小。
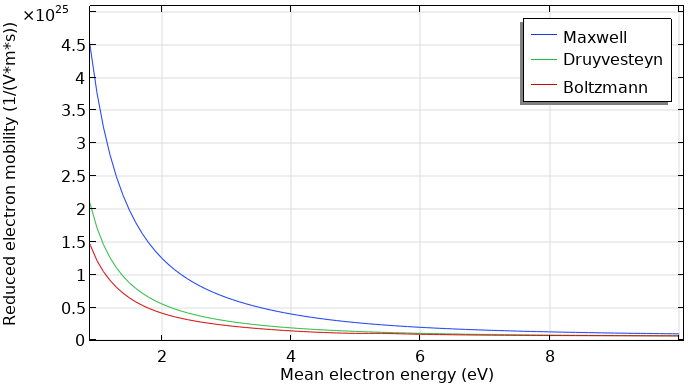
使用不同的能量分布函数计算的下降的电子迁移率。
介质阻挡放电仿真结果的比较
虽然速率系数可以在数量级上有所不同,但我们必须清楚,当改变电子能量分布函数时,宏观量和平均量的趋势不会发生大的变化。想要详细了解这一过程,您可以参阅 COMSOL 案例库中的介质阻挡放电(DBD)模型案例教程。这个模型模拟了常压氩气中的电击穿过程。
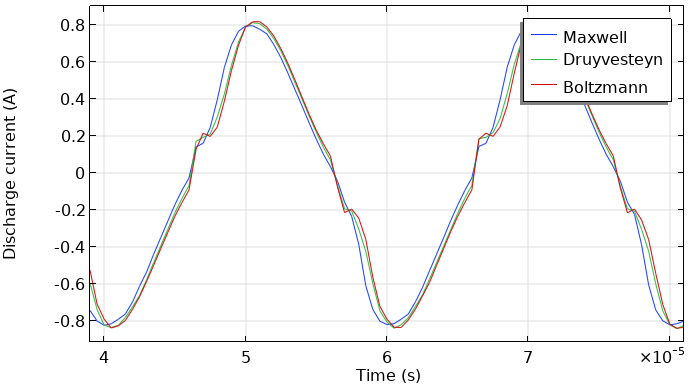
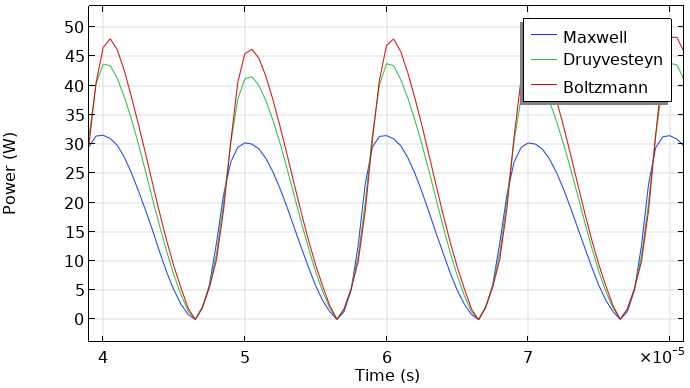
这里用三种不同的电子能量分布函数对该模型进行了重新计算,并对结果进行了比较。下面两幅图显示了在接地电极上的总电流和等离子体中瞬时吸收的功率。等离子体是由频率为50 kHz的正弦电压驱动的。这些数据显示了两个时期的行为。这些结果看起来非常相似。因此,电子能量分布函数的选择会影响建模结果,但不是数量级的(在本例中,系数远小于2)。当然,这取决于您希望提取的模型和特定结果。
介质阻挡放电过程中的总放电电流与时间的函数(左)。介质阻挡放电的吸收功率与时间的函数(右)。





评论 (0)