
在上一篇博客中,我们向您介绍了不同种类的电子能量分布函数 (EEDF)以及它们在等离子体建模中的重要性。今天,我们将通过 COMSOL 案例库中的一个示例模型,演示 玻尔兹曼方程,两项近似 接口的使用方法。
编者注:原博客发布于 2015 年 4 月 8 日,更新于 2022 年 2 月 24 日,以反映 COMSOL Multiphysics® 软件 6.0 版本的新功能。随后,又增加了概念验证模型和其他学习资源的链接。
玻尔兹曼方程,两项近似接口简介
在等离子体模型中,需要电子能量分布函数以及电子传递属性(例如,电子迁移率)。对于最简单的情况,可以使用麦克斯韦电子能量分布函数和电子迁移率的常数值。然后使用爱因斯坦关系在 COMSOL Multiphysics 中计算其他传递属性。然而,在某些情况下,使用从玻尔兹曼方程的解中获得的电子能量分布函数并将电子传递属性定义为平均电子能量的函数可能是有利的。但是我们如何获得这些数据呢?
答案是:使用 COMSOL Multiphysics 中的 玻尔兹曼方程,两项近似 接口。COMSOL 案例库中提供了如何使用此接口的一些示例,其中一个案例是氩气玻尔兹曼分析模型。为了计算二项近似中的玻尔兹曼方程,需要等离子体的电离度等参数。这些参数是 事先未知 的。因此,该过程是一个迭代过程。
该过程首先对参数进行初始估计并求解玻尔兹曼方程。然后,如果需要,将麦克斯韦电子能量分布函数和电子传递属性导入等离子模型。最后,计算等离子体模型,并利用等离子体模型的新参数重新求解玻尔兹曼方程。您可以继续重复这些步骤,直到达到收敛。
接下来,我们将介绍创建、导出和导入数据到等离子模型的步骤。
电子能量分布函数和电子传递属性
从玻尔兹曼方程,两项近似接口创建数据
第一步是通过在两项近似中求解玻尔兹曼方程来创建数据。下图显示了用于此步骤的玻尔兹曼方程、两项近似 接口的屏幕截图。您需要为电子能量定义一个恒定的最大能量。在我们的示例中,它被设置为 Emax= 100 V。此外,您还需要定义一个平均能量 研究来计算一系列平均电子能量的电子能量分布函数。
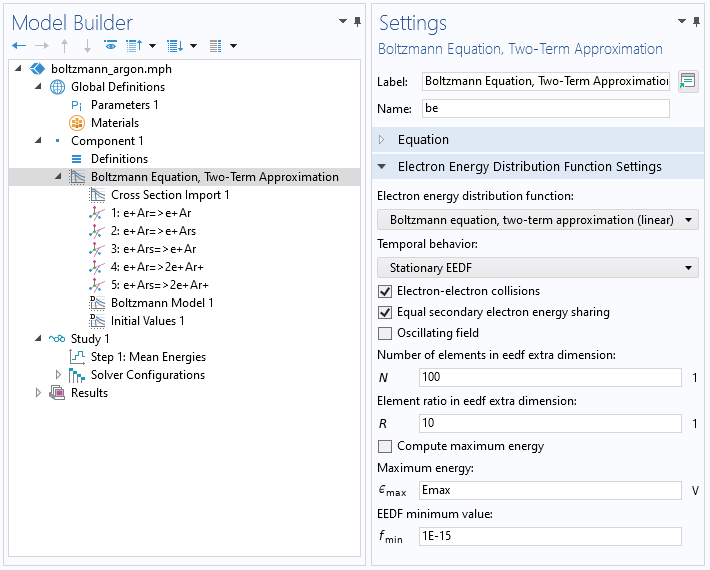
截图显示了 玻尔兹曼方程,两项近似 接口的设置
下图显示了在氩等离子体中计算的几种平均电子能量分布函数。该等离子体气体温度为 400 K,电子密度为 1018 1/m³,电离度为 10-6,激发态氩原子的摩尔分数为 0.01%。可以看出,电子能量分布函数是电子能量的函数。
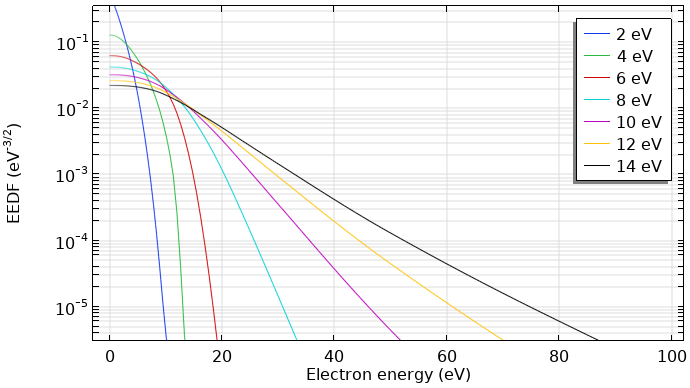
在氩等离子体中计算的电子能量分布函数。
下图描述了使用玻尔兹曼方程,两项近似 接口计算约化后的电子传输特性。该数据是平均电子能量的函数。
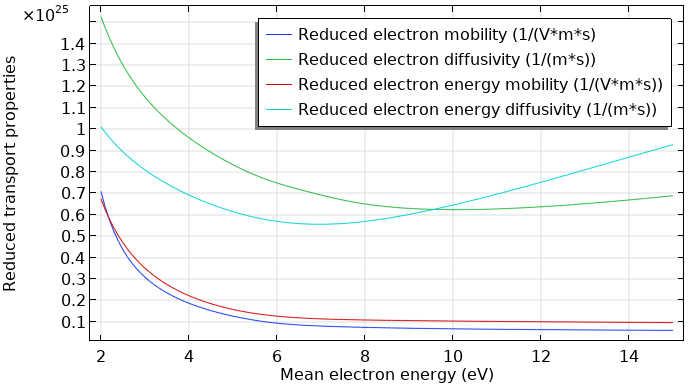
氩等离子体中约化后的电子传输特性。
从玻尔兹曼方程,两项近似接口导出数据
平均电子能量分布函数必须作为一个由三行组成的电子表格导入等离子模型。第一行(x 轴 数据)必须是电子能量(eV),而第二行(y 轴 数据)必须是平均电子能量(eV)。同时,第三行必须包含分布函数 (eV^(-3/2)) 的值。最后,您需要导出如下图所示的二维图。
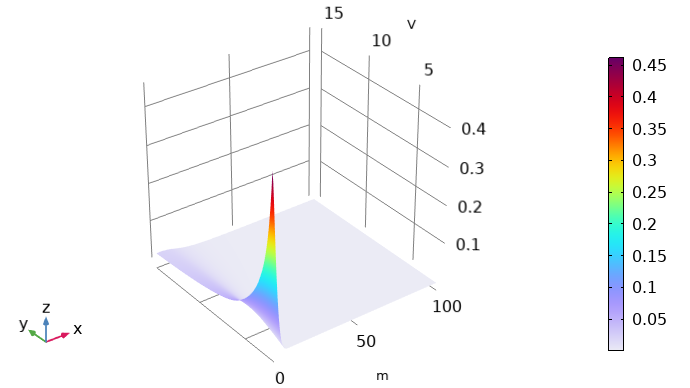
计算的平均电子能量分布函数的二维图。这里,x 轴表示电子能量,y 轴表示平均电子能量。颜色用于说明分布函数的值。
单位注意事项:在等离子模块中,电子能量和电子平均能量的单位为 V,但在内部被视为 eV。因此,这里 V 应理解为 eV。代表电子能量并在其上求解平均电子能量分布函数的额外空间维度的单位为米,但在内部被视为 eV。
如果要用您所需要的格式导出平均电子能量分布函数,请使用 参数化拉伸 数据集。参数拉伸使用参数(在这种情况下为平均能量)扩展数据集。右键单击 数据集 并选择一维参数化拉伸。
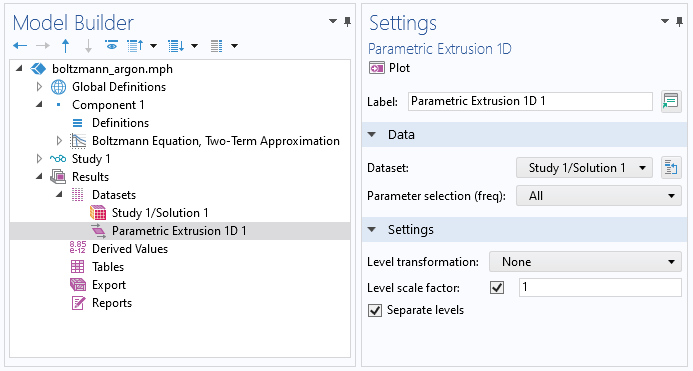
截图显示了 一维参数化拉伸 数据集的设置。
玻尔兹曼方程,两项近似 接口是零维的,并使用额外的维度来表示一维轴上的电子能量。由于额外维度被归一化为 最大能量 值,因此必须在导出数据之前使用最大能量值 手动缩放。为此,我们可以使用 变换 数据集。使用变换 数据集,可以缩放、旋转和移动数据集。因此,右键单击数据集 并选择变换二维。将x轴设置为最大能量(本例中为 Emax)。
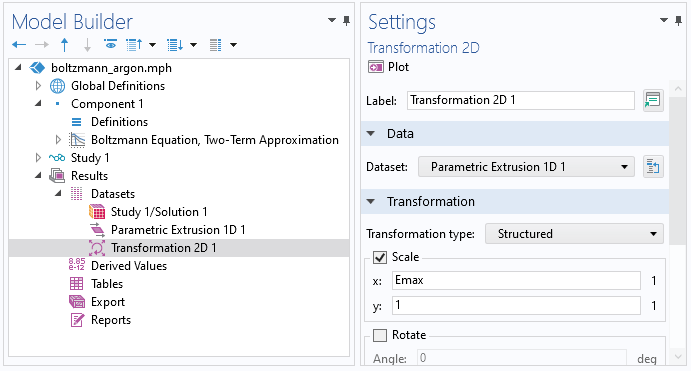
截图显示了 变换二维 数据集的设置。
然后,右键单击 变换二维 数据并选择 添加要导出的数据。在表达式 窗口中输入 be.f。选择文件名并单击导出。
可以从相应的一维绘图直接导出传递属性。右键单击一维绘图中的 全局节点,然后选择 添加要导出的数据。选择文件名并单击导出。
将数据导入等离子体模型
为了将电子能量分布函数导入等离子模型,需创建插值函数。选择文件 作为数据源并在变元数 字段中输入 2。单击 浏览 并导入文件。
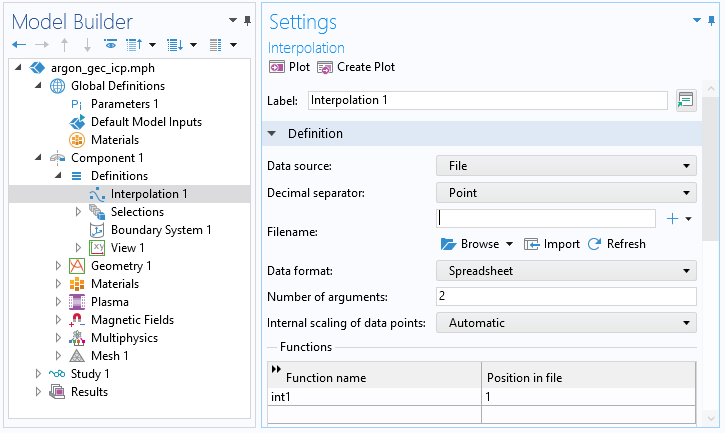
截图显示了 插值 函数的设置。
完成这个操作后,您可以在等离子模型主节点的电子能量分布函数 设置中选择插值函数作为电子能量分布函数。如下面屏幕截图所示。
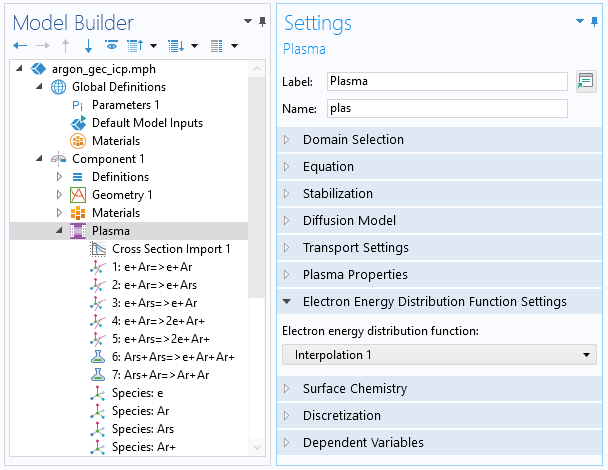
截图显示了 等离子体 接口的设置, 需要考虑事先计算的电子能量分布函数(EEDF)。
传递属性的函数,例如电子迁移率和扩散率,也可以作为插值函数导入。本案例中的参数数量为 1。在等离子体模型节点中,您可以通过输入 int2(plas.ebar) 来使用这个插值函数。在这种情况下,int2 是函数的名称,plas 是接口的标记, ebar 是平均电子能量。
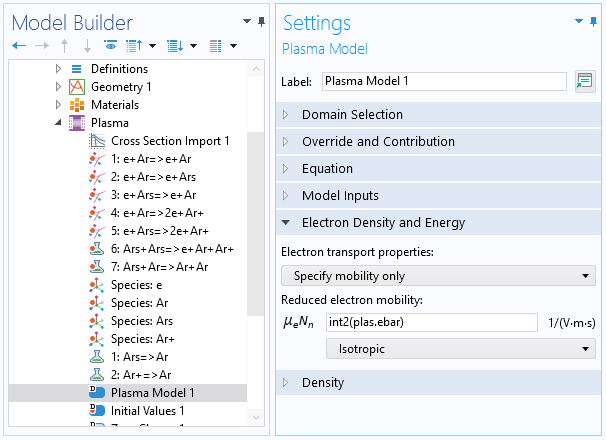
截图显示了等离子体模型 节点的设置, 需要考虑事先计算的约化电子迁移率。
下一步
从 COMSOL 案例库中下载使用不同 EEDF 计算的介质阻挡放电模型,尝试使用本文中推荐的方法模拟。
延伸阅读
浏览相关的资料,了解在 COMSOL Multiphysics® 中使用不同 EEDF 计算和处理的方法:
- 博客: 电子能量分布函数
- 博客: 使用 COMSOL® 对非麦克斯韦放电进行全局建模
- 教程模型: 与两项玻尔兹曼方程耦合的直流辉光放电
您也可以查阅我们的博客,了解 COMSOL® 中用于不同类型等离子体建模的不同方法,或者 COMSOL 学习中心专门开设的非平衡等离子体仿真的在线课程:
- 博客: 等离子体的热力学平衡
- 学习中心课程: 非平衡等离子体仿真简介






评论 (0)