
今天我们继续讨论弱形式,看看如何用弱形式实现点源。点源是一个有用的工具,可以将聚集在建模域内的一个非常小区域的源进行理想化表述。阅读完这篇文章之后,您将会发现,用弱形式建立这种点源非常方便。
点源的数学基础
考虑一个在 x 轴上的一维域,源位于 x=0 附近。我们可以把源的强度绘制成 x 的函数,如下图所示:
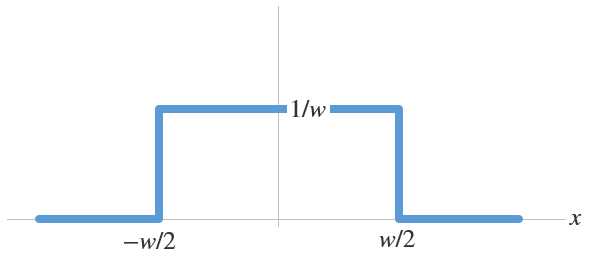
这里,我们假设强度值在区间 [-w/2, w/2] 内,1/w 保持不变,在其他位置都为零。如上图所示,我们可以描绘出一个宽度为 w,高度为 1/w 的矩形形状。该函数通常被称为矩形函数(rectangular)、顶帽函数(top-hat),有时也被称为圆盘函数(disc function)。源的总强度可以由矩形的单位面积计算。
对于线性系统,如果我们只关心离源较远的地方会发生什么,即 \left| x \right| \gg w,那么源强度的实际形状并不重要,只要该形状下的面积是相同的就可以。此外,我们可以自由地使 w 逐渐变小:矩形的宽度减少,高度增加,以使总面积保持不变,如下图所示。
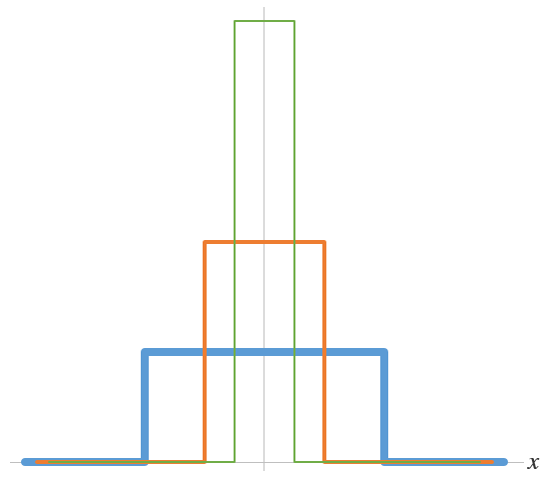
蓝色曲线所代表的局部源被逐渐变细和变高(橙色和绿色曲线),同时保持积分强度为单位面积。
最终,我们得到一个无限薄、无限高的矩形,但仍有一个定义明确的单位面积。由此,我们得到一个 δ 函数 \delta (x),相应地,局部源现在变成了一个理想化的单位强度的点源。
δ 函数有一些方便的特性。除了原点,它的值在任何地方都是零。
\infty \mbox{ for } x=0\\
0 \mbox{ elsewhere}
\end{array} \right.
对 δ 函数和另一个函数的乘积进行积分,其实就只是提取后者在原点的函数值。
对于一般位置上的点源 x=a,可以通过 δ 函数的简单的坐标移动得到 \delta(x-a)。于是有
\infty \mbox{ for } x=a\\
0 \mbox{ elsewhere}
\end{array} \right.
和
将 δ 函数和相应的点源推广到更高的维度也是很容易的。例如,对于二维,我们有
\infty \mbox{ for } x=a, y=b\\
0 \mbox{ elsewhere}
\end{array} \right.
和
(1)
使用弱形式实现点源
点源实现教程求解了点源位于原点的单位圆盘上的泊松方程。该方程为
(2)
其中,u 是要求解的相关场变量。
乍一看,如何将这个方程离散化进行数值求解可能并不明显。将等式右边的源项在原点设置什么值合适?δ 函数的值在那里是无限的,但计算机不喜欢无穷大的值!
这时,弱形式公式就能派上用场了。记得在关于弱形式概述的博客中,我们把要求解的微分方程乘以一个测试函数,并在整个域上进行积分(见该文中的公式(4))。本文,我们可以按照同样的程序来求解方程(2)。在乘以测试函数 ,并在统一圆盘域上积分后,方程(2)等式右边就变成了
(3)
这为我们在 COMSOL Multiphysics 中的实现提供了一个非常容易的形式。
使用弱形式偏微分方程 物理场接口和一个瞬态研究建立一个新的二维模型,开始我们的研究。画一个以(0,0)为中心的单位圆,并在那里也画一个点。将默认的弱形式偏微分方程 1 特征下的弱表达式字段设置为 -test(ux)*ux-test(uy)*uy。这与上一篇博客中讨论的一维情况完全一样,将公式(2)等式左边的项转换为了弱形式。
现在,对于右边的点源 \tilde{u}(0,0),只需添加一个点弱贡献节点,并选择原点。对于弱表达式,输入 test(u)。对于点源来说,就是这么简单!
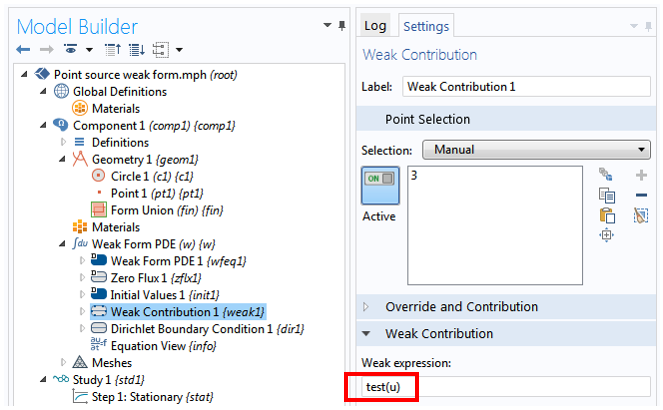
值得注意的是,通过输入 test(u),将点源的强度设置为单位面积。对于任何其他源的大小,只需要乘以一个系数即可。例如,表达式 2*test(u) 表示一个强度为 2 的点源。
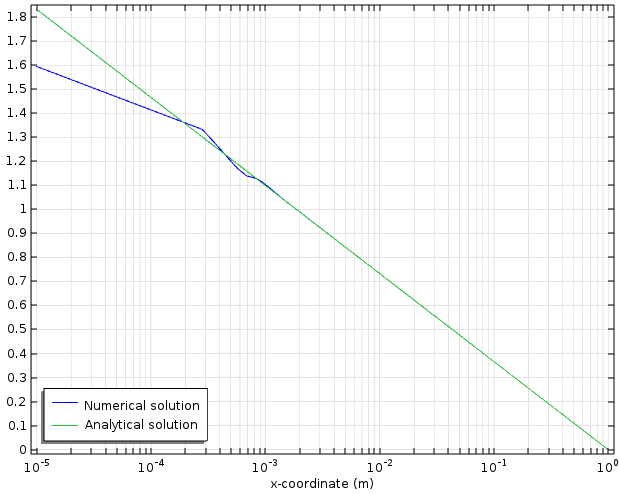
在圆周上用狄利克雷边界条件完成设置后,我们就可以求解这个模型,并得到与上面提到的点源教程模型中相同的解。
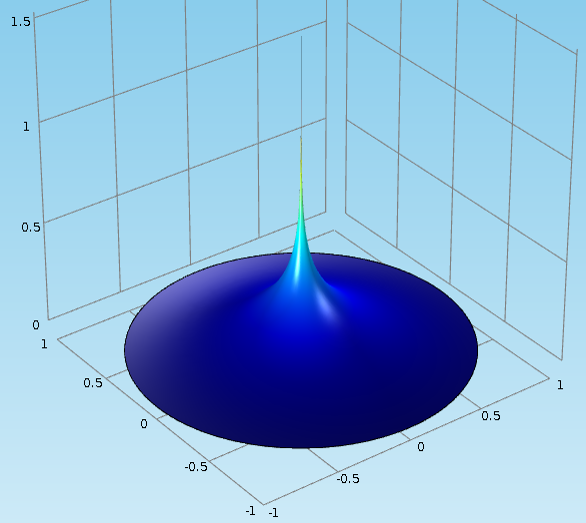
同样,如教程中所看到的,数值解(蓝色曲线)与解析解(绿色曲线)非常吻合,除了在原点附近出现了奇点。
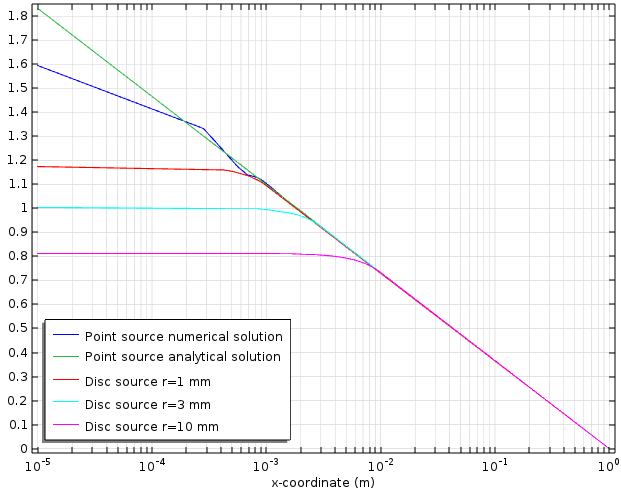
如前所述,在只对离源较远的解感兴趣的情况下,点源对局部源提供了一个方便的理想化表述。我们用下图来说明,在上图中又增加了三条曲线。这三条曲线是同一单位圆盘域中同一泊松方程的数值解,但用不同大小的顶帽或圆盘状的源代替了点源。每个顶帽源的积分强度被校准为单位面积,方法是将其高度设置为1除以其覆盖面积,与上图所示的一维情况相同。如下图所示,所有的解在远离源的位置都是非常接近的。(在这个例子中,x \gg 10 \, mm。)
结语
这篇文章我们证明了使用弱形式创建点源的方便性。通过简单的积分避免了使用 δ 函数表示的数值计算困难。在接下来的文章中,我们将研究非连续和边界条件。请继续关注!



评论 (0)