
在设计电磁线圈时,我们可能想要调整线圈的位置,以便在特定的空间区域内获得所需的磁场强度。这可以使用 COMSOL Multiphysics® 软件附加的“AC/DC 模块”和“优化模块”产品,结合参数和形状优化来实现。接下来,让我们看看如何操作。
初始线圈设计和优化问题
假设我们的任务是设计一个线圈,使沿着部分中心线的磁场尽可能接近目标值。我们在之前的博客文章中介绍过,可以通过调整每匝线圈的电流来实现,但是,文中讨论的方法要在设计方案中为每匝线圈设计单独的电流控制。其实,我们可以对整个线圈使用单一的电流控制,并沿轴向调整线圈的间距来实现。
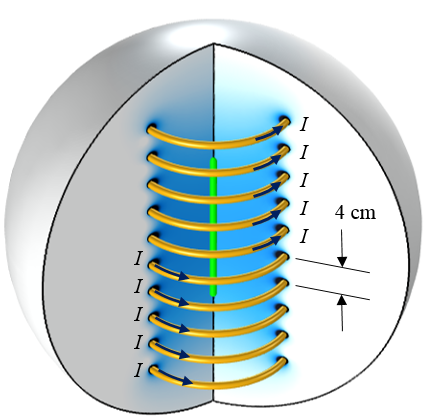
10 匝轴对称线圈。目标是改变中心线(绿色)处的磁场。
上图所示的线圈就是我们将要分析的案例。10 匝轴对称线圈由单个电流源驱动; 也就是说,流经每匝线圈的电流相同。最初的线圈设计将直径为 1cm 的线圈间隔为 S0 = 4cm 的距离。由于线圈是轴对称结构(我们仅对关于 z = 0 平面对称的解感兴趣),我们可以使用下图所示的简化计算域。
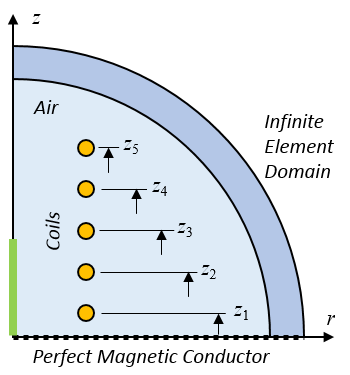
计算模型。我们想要改变五个线圈的位置和线圈电流。
我们的优化目标是通过改变五个线圈的线圈电流和 z 位置,使沿着一部分中心线的 Bz 场尽可能接近期望值 B0。每个线圈可以移动的距离为 ,相邻线圈之间必须存在 G0 的间隙,因此第一个线圈的偏移量具有不同的下限。我们还需要对峰值电流进行约束,将电流限制在大于零的范围内。虽然从物理上讲,没有必要将电流限制在大于零的范围内,但这样做是一个很好的优化建模的技巧,因为这样可以保持受限的设计空间更小。
更正式地讲,这些陈述可以写成:
\int_0^{L_0} \left( \frac{B_z}{B_0}
-1 \right) ^2 d l \\\end{aligned}
& \text{subject to:}& & -(S_0-G_0)/2 \le \Delta Z_1 \leq \Delta Z_{max} \\\end{aligned}
& & & -\Delta Z_{max} \leq \Delta Z_2, \ldots ,\Delta Z_5 \leq \Delta Z_{max} \\\end{aligned}
& & & G_0 \le (Z_5-Z_4) \\\end{aligned}
& & & G_0 \le (Z_4-Z_3) \\\end{aligned}
& & & G_0 \le (Z_3-Z_2) \\\end{aligned}
& & & G_0 \le (Z_2-Z_1) \\\end{aligned}
& & & 0 \leq I \leq I_{max}\\\end{aligned}
我们通过使用 COMSOL Multiphysics 中的优化 和变形几何 接口,结合参数和形状优化来求解这个问题。
在 COMSOL Multiphysics® 中建立和求解优化问题
我们可以先看一下这篇文章中针对特定的物理场值进行优化的模型。使用上一篇文章中介绍的相同的优化 接口和积分目标 特征开始操作。然后使用两个全局控制变量 特征。第一个特征设置五个线圈的位移,使用控制变量尺度 优化变量缩放到接近于 1 的。第二个全局控制变量 特征,用类似的方法定义和约束电流。
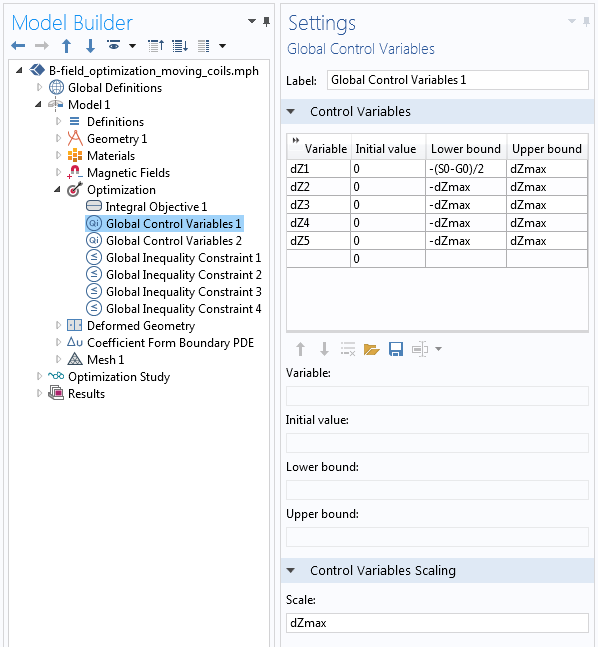
控制五个线圈位置的变量及定义。
上图中显示的五个控制变量 定义了线圈的位移,以及每匝线圈周围的一小块方形空间区域,如下图中绿色域所示。当这些绿色域上下移动时,周围的黄色域必须伸展和收缩来适应这种情况,而周围的蓝色域保持不变。我们知道绿色域的位移,因此可以指定沿着所有红色边的位移的线性变化。这种线性位移变化可以使用系数形式边界偏微分方程 接口进行计算,就像之前关于平移运动建模的文章所介绍的那样。
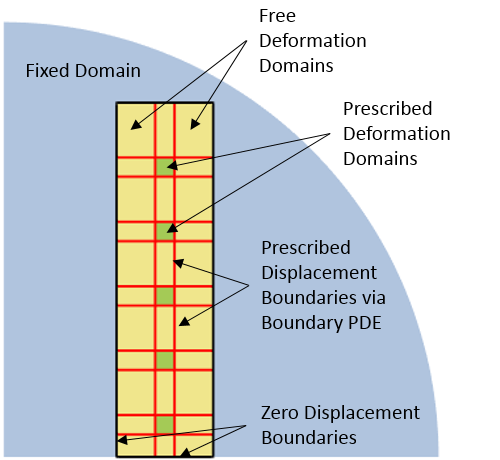
模型中各个域的变形示意图。
如下面的屏幕截图所示,使用变形几何 接口设置有关各个域的指定位移信息,如下面的屏幕截图所示。使用指定变形 域功能移动绿色域,用自由变形 域允许黄色域变形。指定网格位移 边界功能施加在黑色和红色边,并完全定义黄色域的变形。
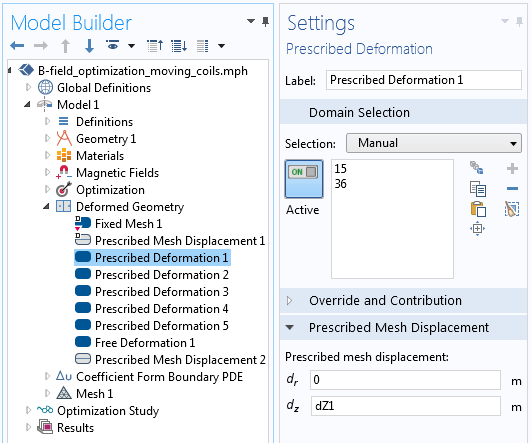
通过 变形几何接口中 的“指定变形”特征控制线圈位移。
以这种方式设置变形几何 接口,最终得到线圈位置的五个控制变量现在用于表示形状优化问题。之前,我们已经使用了一个更通用的结构力学案例讨论了形状优化。形状优化利用了 COMSOL Multiphysics 计算设计方案对几何形状发生变化的敏感性。
我们还需要定义一组全局不等式约束,来阻止线圈周围的绿色域彼此过于靠近并相交。下面的屏幕截图显示了如何在COMSOL中实现这个操作。请注意,根据间隙大小 G0 缩放约束,以使约束方程在大小上也接近1。
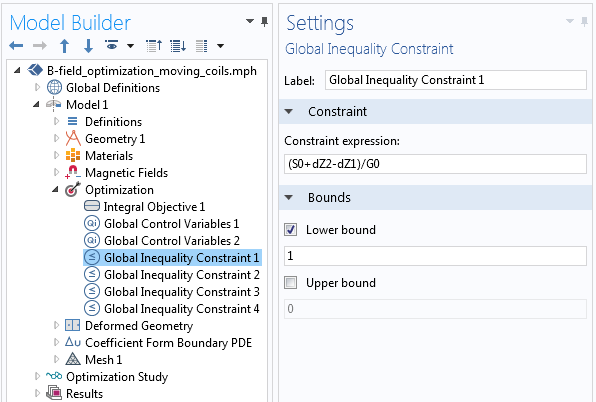
保持线圈相互不要靠得太近的四个约束之一。
由于拉伸和收缩线圈周围的域中可能发生大的变形,因此使用映射网格也很有帮助。
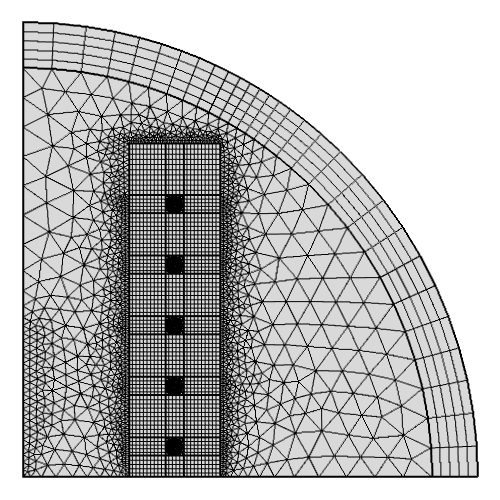
映射网格用于线圈周围的变形域。无限元域也有一个映射网格。
然后,我们可以利用通过解析方法计算的梯度,使用基于梯度的优化求解器(SNOPT)来求解这个问题。调节通过线圈的电流和线圈位置来使上述目标函数最小化。优化结果如下图所示。
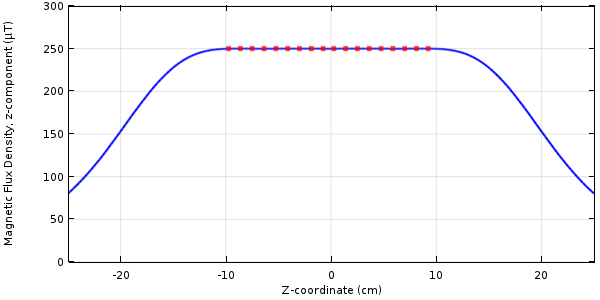
沿优化线圈中心线的磁通密度 z 分量。
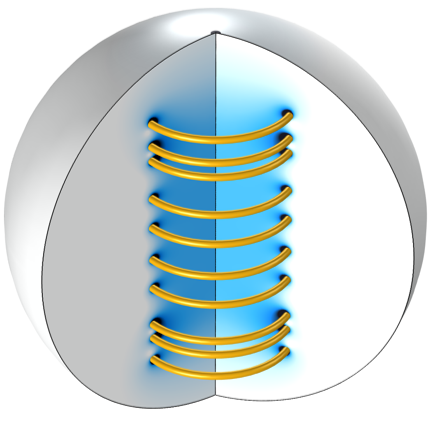
优化的线圈位置。
优化电磁线圈间距的结论性思考
我们介绍了一个使用形状和参数优化组合来调整二维轴对称线圈中的线圈电流和线圈间距的模型。通过利用优化 和变形几何 接口,我们能够用解析方法计算这个问题的导数,并可以非常快地收敛到最优值。






评论 (0)