模拟大功率激光系统中的热致焦移

几乎所有介质都会在一定程度上吸收电磁辐射。在大功率激光聚焦系统中，玻璃透镜等介质可能会从激光中吸收足够的能量而明显升温，从而导致热变形并改变材料的折射率。反过来，这些扰动也可以改变激光传播的方式。使用 COMSOL 附加的射线光学模块，您可以创建一个完全合理的，包括热效应和结构效应的激光传播模型。

热透镜的原理

要了解射线轨迹如何受自感温度变化的影响，可以考虑一束以垂直入射方式撞击玻璃板的准直光束。假设玻璃表面添加了抗反射涂层，不会反射光线。一块玻璃板吸收传输光束的一小部分（不为 0）能量。如果功率足够低，玻璃内的温度变化可以忽略不计，出射光将与入射光平行。

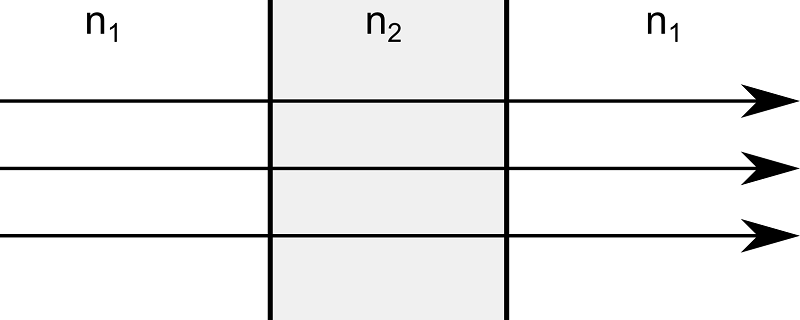
然而，如果是大功率的光传输，玻璃板吸收的能量可能会明显改变玻璃的温度。玻璃略微膨胀，改变了光的入射角，并导致透射光偏离它们最初平行的轨迹。此外，许多材料具有与温度相关的折射率，温度引起的折射率变化也会扰乱光线轨迹。由于结构变形和折射率的变化趋向于使出射光线聚焦，这种现象被称为热透镜。

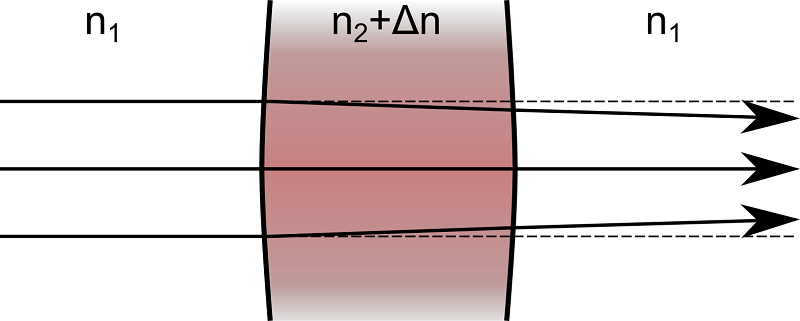
接下来，我们将更深入地研究热效应和结构效应会明显扰乱射线轨迹的应用。

模拟激光聚焦系统

考虑一个由两个平凸透镜组成的基本激光聚焦系统。第一个透镜准直光束的输出，第二个透镜将准直光束聚焦到一个小目标。

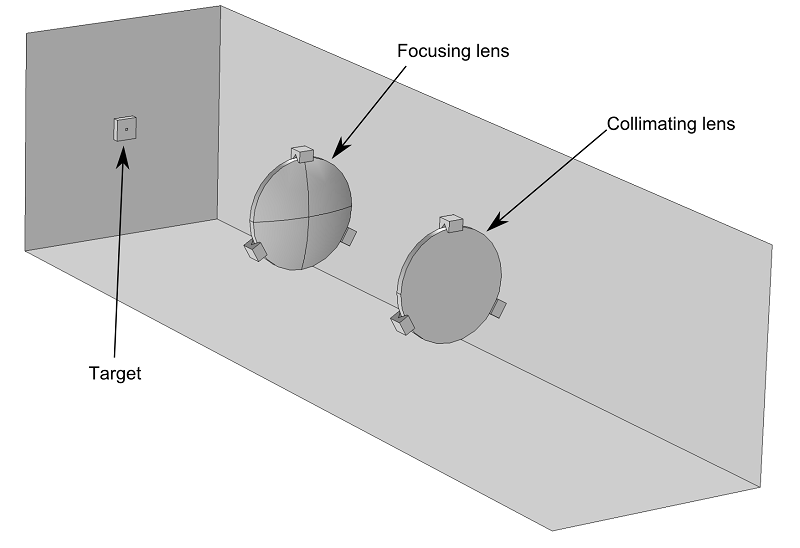
如果激光束提供少量功率，就可以直接使用以下方法对光束向目标的传播进行建模。使用几何光学 接口，并忽略透镜的温度变化。下图显示了光线在透镜系统中的轨迹。

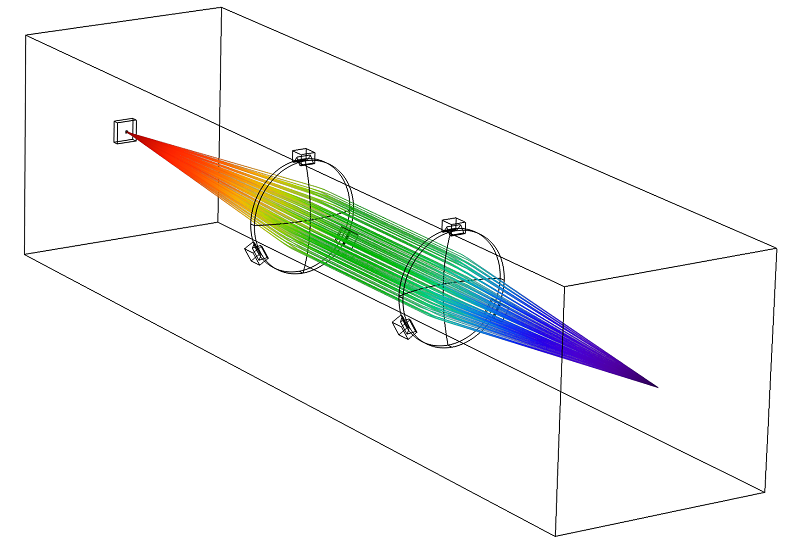
然而，即使是高质量的玻璃透镜也会吸收一小部分穿过它的电磁辐射。如果光束传输非常大的功率，则有可能发生热致焦移；换句话说，折射率和透镜形状的变化可以明显移动光束的焦点。 如果需要精确聚焦激光，那么在设计透镜系统时必须考虑热引起焦距偏移的可能性。

在这个示例中，我们将观察透镜中的温度变化如何导致光束聚焦在距目标几毫米的位置。

吸收介质中的射线传播建模

为了模拟热变形透镜系统中的光线传播，我们使用以下物理场接口:

• 几何光学 — 计算射线轨迹。
• 固体传热 — 计算透镜中的温度。
• 固体力学 — 模拟透镜的热膨胀。
• 动网格 — 使与透镜相邻的域中的有限元网格变形。

这个模型中使用的物理场接口和节点如下面屏幕截图所示。

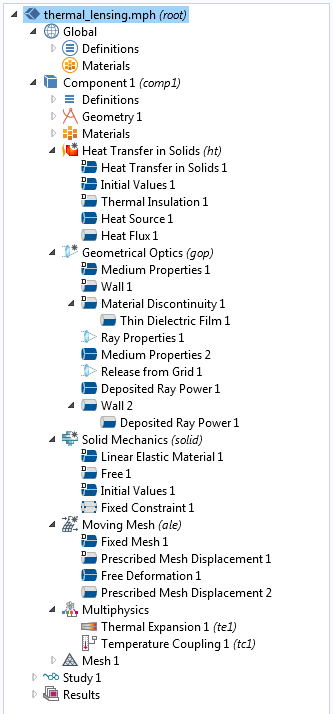
除了射线光学模块之外，还需要结构力学模块或 MEMS 模块模拟透镜的热膨胀。

射线轨迹计算

在软件中，射线光学模块通过求解一组耦合的一阶常微分方程来计算光线轨迹,

(1)

式中，\mathbf{q} 是光线位置，\mathbf{k} 是波矢量，\omega 是角频率。 波矢量和角频率的关系为

(2)

式中，c 是真空中的光速。 在吸收介质中，折射率可以表示为 n-i\kappa，其中 n 和 \kappa 是实数。

当光线进入和离开透镜时，根据斯涅尔定律，它们会发生折射,

(3)

式中，\theta_1 和 \theta_2 分别是入射角和折射角。

使用菲涅尔方程计算折射光线的强度和功率。 在大多数工业激光聚焦系统中，在透镜表面涂有抗反射涂层，用于防止反射大量辐射。

在这个示例中，通过将介电薄膜节点应用于透镜表面来模拟抗反射涂层。

计算每条射线传输的功率

用于计算射线强度的变量由几何光学接口 设置窗口中的“强度计算”组合框控制。要使用射线损失的能量计算热源，请选择“使用主曲率和射线功率”。

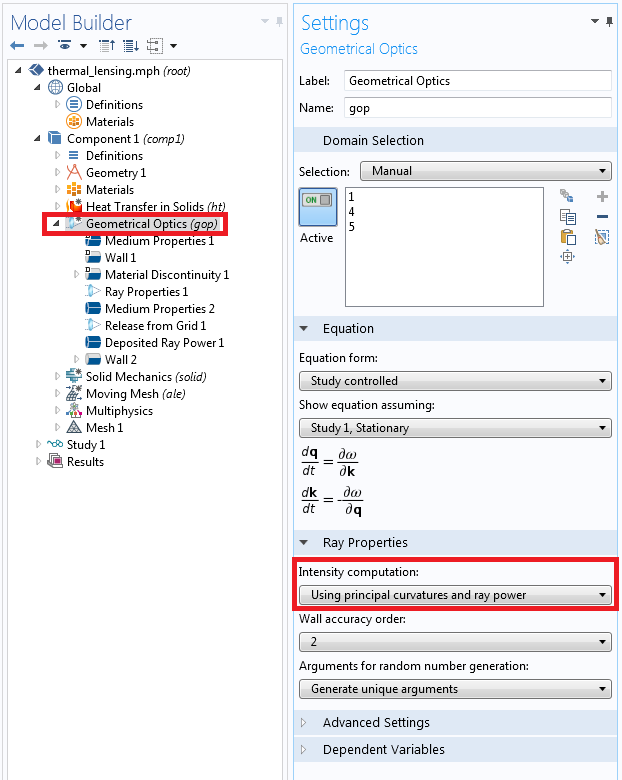
每条光线传输的总功率 Q，在非吸收域中保持不变。在均匀的吸收域中，功率呈指数衰减,

(4)

式中，k_0 是射线的自由空间波数。

为了将由光线的功率损失用作固体传热 接口的源项，有必要在吸收域中添加一个沉积射线功率节点。 对于由于所选域中的射线衰减引起的体积热源，这个节点定义了一个变量 Q_{\textrm{src}}（国际单位：W/m^3)。 当光线通过透镜传播时，它们对 Q_{\textrm{src}} 值有贡献,

(5)

式中，Q_{j}（SI 单位：W）是某条光线的传输的功率，j 是光线的总数，j 是狄拉克函数。实际上，每条射线不能在其精确位置产生热源项，因为射线在空间中占据无限小的点，而底层网格单元具有有限大小，因此每条射线损失的功率均匀分布在射线所在的网格单元上。

下面的简短动画说明了在域网格单元（上）上定义的热源如何随着每条射线（下）传输的功率减少而增加。

计算温度

透镜的温度 T，可以通过求解传热方程来计算,

(6)

式中，k 是介质的热导率。使用热通量节点在暴露于周围空气的所有边界处施加对流冷却,

(7)

结构变形

随着温度的变化，它对透镜中的总非弹性应变贡献了一个热应变项 \epsilon_{\textrm{th}}。 热应变定义为

(8)

式中，\alpha 是热膨胀系数，T 是介质的温度，T_{\textrm{ref}} 是参考温度。产生的位移场 \mathbf{u} 由固体力学接口 计算。

获得合理的解

如果光束传输的功率非常低，则光线损失到周围环境的能量不会明显改变介质的温度。但是如外力和热源等其他现象，仍然有可能改变透镜的形状或温度。

在这个案例中，需要先计算域内的位移场和温度，然后再计算射线轨迹。这被认为是一个单向，或单向耦合，因为温度变化和结构变形会影响射线轨迹，但反过来却不是这样。

如果光束传输的功率足够大，吸收介质中的能量耗散可能会产生足够的热量，从而显著改变区域的形状或介质中的折射率。在这个示例中，光线轨迹会影响在周围域上定义的变量，例如温度，而这些变量又会影响光线轨迹，这是一个双向，或双向耦合。

在这个示例中，我们假设激光器以恒定功率运行，因此最好使用稳态研究步骤来计算温度和位移场。但是，射线轨迹是在时域中计算的。

为了在射线轨迹与温度场和位移场之间建立双向耦合，我们首先创建一个稳态研究步骤来模拟透镜的加热和变形，然后添加一个射线追踪研究步骤来计算射线轨迹。然后，使用 For 和 End For 节点将相应的求解器封闭在一个循环中。下图显示了用于在射线轨迹与温度场和位移场之间建立双向耦合的求解器序列。

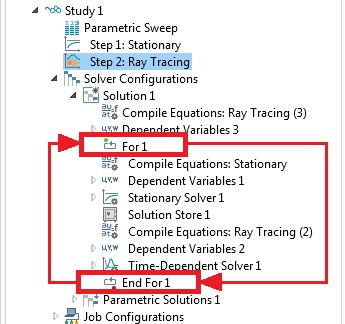
For 和 End For 节点之间的节点将重复 For 节点的设置窗口中指定的次数。 此外，每次运行求解器时，它都会使用前一个求解器的解。 通过这种方式，可以在两个研究之间建立双向耦合，并在它们之间进行迭代，直到获得合理的解。

热透镜模拟结果

现在检查在两种不同的功率：1w 光束和 3000w 光束下，靠近目标的射线轨迹

对于 1w 的光束，我们观察到光束的焦点非常靠近目标表面。由于球面像差，光线不会聚到一个点. 对于 3000w 的光束，我们看到光束到达目标表面时已经开始发散。 下图比较了两种情况下目标处的沉积射线功率。

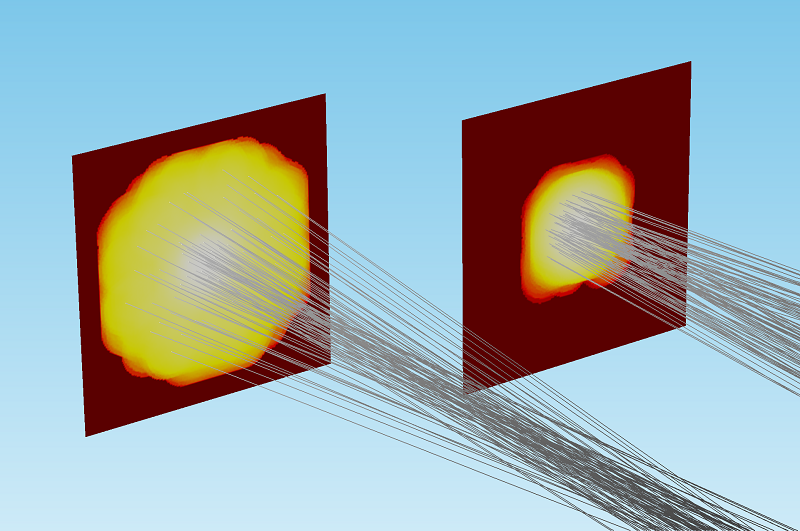
3000w 光束（左）和 1w 光束（右）沉积射线功率的比较。 为了进行比较和可视化，沉积功率的颜色表达式已被归一化并用对数尺度表示。

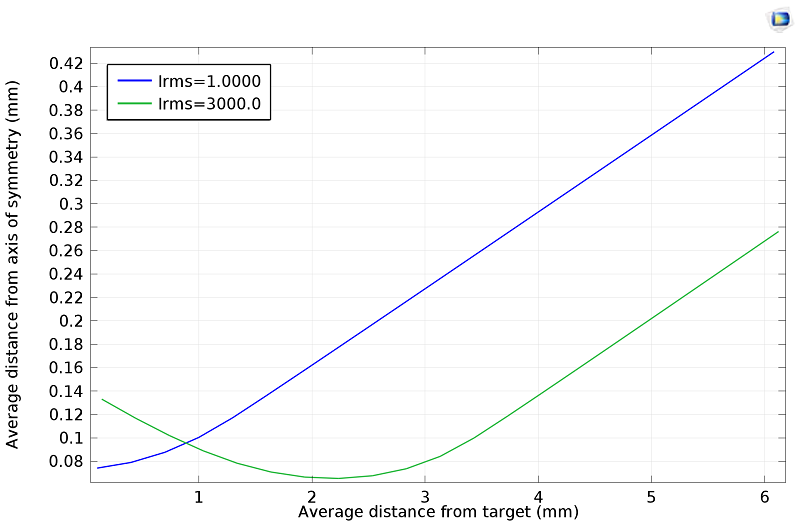
几何光学 接口还包括内置算子，用于计算所有光线的表达式的总和、平均值、最大值或最小值。使用这些算子，可以通过多种方式量化波束宽度。如下图所示，3000w 的光束聚焦在距离目标表面 2mm 以上的地方。

我们已经看到，大功率激光系统中的温度变化和由此产生的热膨胀会明显改变光束的焦点。使用射线光学模块，您在设计此类系统时可以考虑热变形引起的焦移。

模型下载

要了解有关在热变形透镜系统中计算光线轨迹的更多信息，请查看大功率激光聚焦系统中的热致焦移模型。