了解齿轮建模的不同因素

要准确模拟一个齿轮并获得有用的结果，重要的是考虑设备设计背后的一些因素以及它们是如何建模的。COMSOL Multiphysics^® 软件的一些新特性和功能为您提供了处理此类特性的工具，从而提高了仿真研究的可靠性。今天，我们将回顾齿轮建模的各种元素，并解释如何在我们的建模过程中考虑它们。

齿轮的简要概述

作为复习，让我们首先回顾一下 COMSOL Multiphysics 中齿轮建模背后的一些关键概念。齿轮在齿轮 节点中被定义为具有六个自由度的刚体，其运动形式为定义在旋转中心的平移和旋转。它被用于模型树中的 齿轮对 节点，以便与另一个齿轮连接。在这里，您可以为单个齿轮或成对齿轮指定齿轮啮合或齿轮齿的有限刚度。使用数学公式描述两个齿轮之间的连接，不需要任何定义的、真实的齿轮几何形状来检测两个齿轮之间的接触。因此，您可以使用实际的齿轮几何图形或任何类似的圆盘几何图形来表示齿轮。

您可以使用计算出的质量密度从几何形状计算齿轮的惯性特性，或者直接在节点的编辑字段中以质量和惯性矩的形式输入这些特性。您还可以在齿轮上施加外力和力矩，也可以约束齿轮的某些自由度。例如，在模拟扭转振动时，除轴向旋转之外的所有自由度都可以受到约束。

齿轮类型的选择

COMSOL Multiphysics 提供了多种标准齿轮类型，每种类型都有自己的优点和应用。正如上面所提到的，齿轮是一个抽象的对象，但如果您想添加逼真的几何图形以进行可视化，您可以访问零件库，在那里您可以找到各种类型的齿轮和齿条。

在下图中，您可以看到各种可用的齿轮和齿条，以及它们的数学描述所需的几何参数。

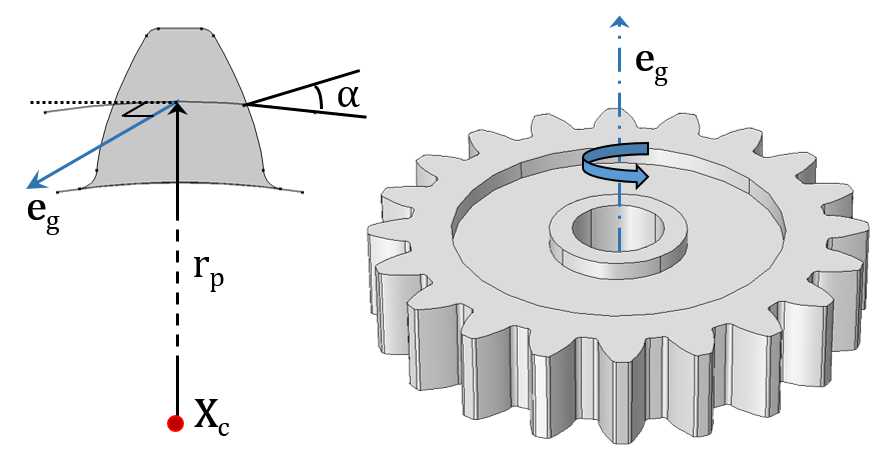
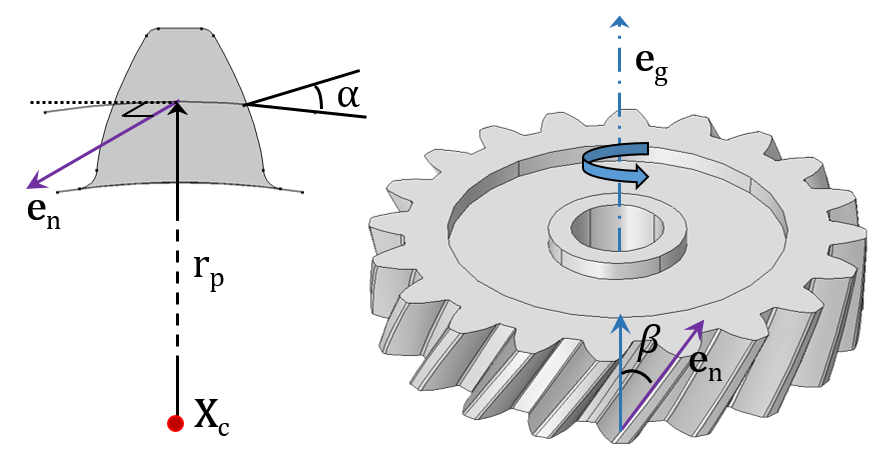
直齿轮(左)和斜齿轮(右)与他们的外接齿轮啮合。

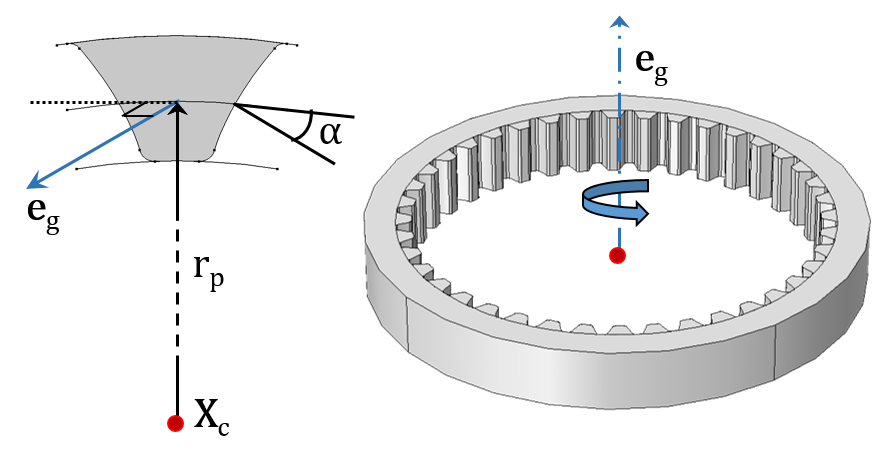
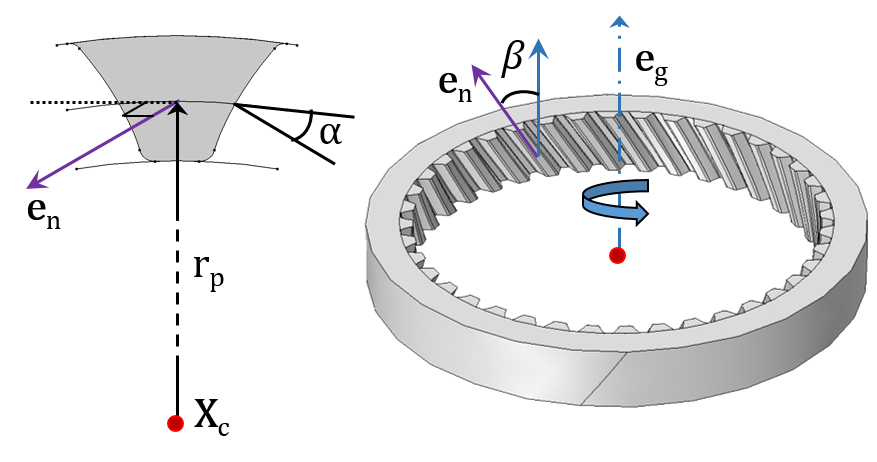
直齿轮(左)和斜齿轮(右)与他们的内部齿轮啮合。

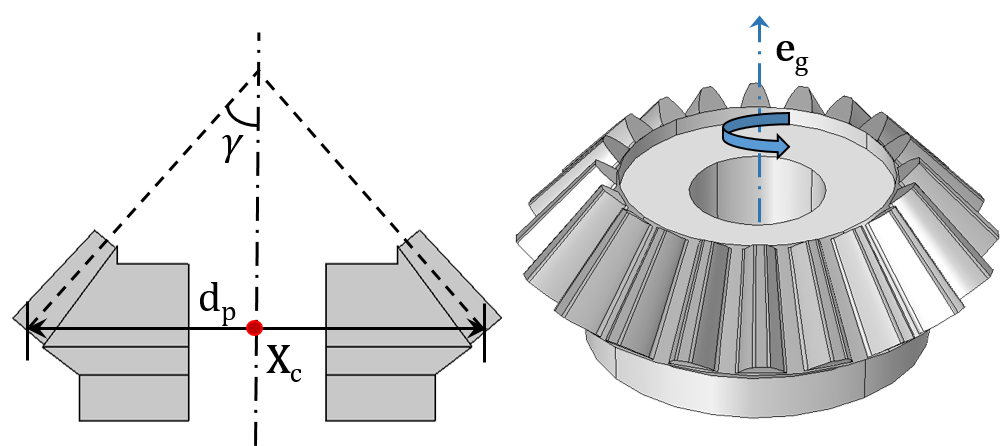
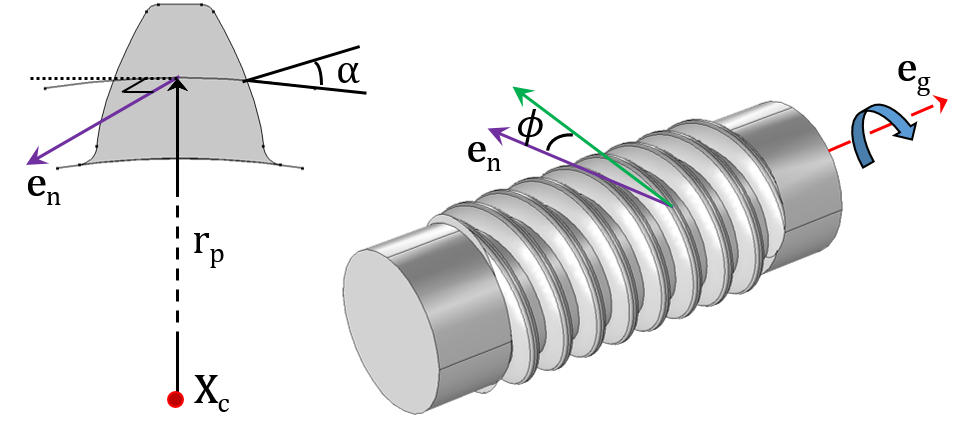
一个锥形齿轮(左)和蜗轮(右)。

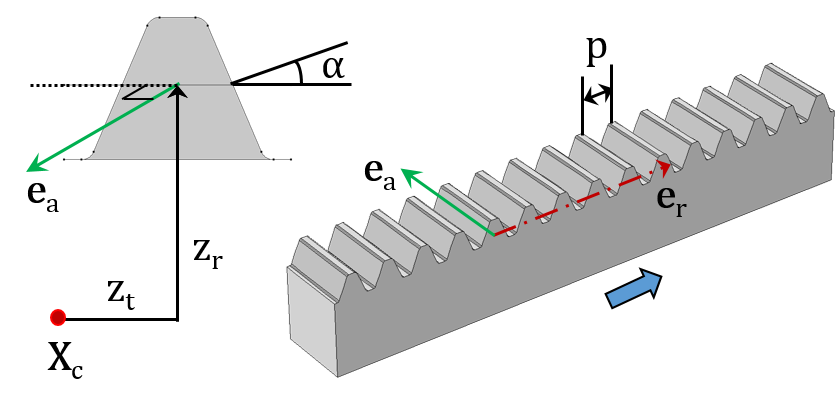
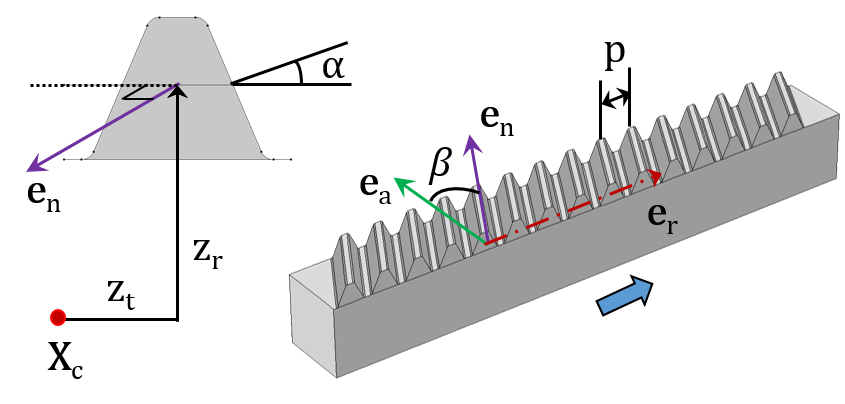
直齿条(左)和斜齿条(右)。

模拟每种齿轮类型所需的输入显示在各自的图表中。如下所示:

• 旋转中心(X_c）
• 齿轮轴(e_g)和齿条轴(e_r）
• 节圆半径(r_p)及节圆直径(d_p）
• 压力角(α)、螺旋角(β)、锥角(γ)，导程角(Φ）
• 端面齿距(p）
• 切向偏移(z_t)和径向偏移(z_r）

定义齿轮齿形参数

在选择适当的齿轮类型后，您可以定义控制齿轮齿的大小和形状的参数。例如，定义斜齿轮需要这些参数：

• 齿数
• 节圆直径
• 压力角
• 螺旋角

显示斜齿轮设置窗口的屏幕截图。显示了模拟斜齿轮所需的各种输入，包括齿轮特性、齿轮轴、旋转中心和密度。

指定齿轮位置和方向

下一步是定义齿轮的位置和方向。齿轮位置是根据旋转中心定义的。在这一点上创建了自由度和并定义旋转。由于与其他齿轮啮合而作用在齿轮上的力和力矩也作用在这一点。默认情况下，旋转中心设置为齿轮的质心，但也可以通过其他方式明确定义它。

齿轮方向是根据齿轮轴指定的，齿轮轴是通过旋转中心的旋转轴。使用齿轮轴创建齿轮局部坐标系。关于这个轴也解释为齿轮旋转，即齿轮对 节点中的一个自由度。

在轴上安装齿轮

你可以安装齿轮在两种方式之一:在一个柔性或刚性轴。这些装置既可以刚性安装，也可以使用固定关节柔性安装。关节是用来连接两个组件的特征，允许它们之间有一定的相对运动。

当几何中的齿轮和轴之间没有间隙时，物体可以处于装配状态或联合状态。对于柔性轴，如果齿轮和轴都处于联合状态，齿轮默认与轴刚性连接。

没有必要为安装齿轮而对轴进行建模，因为这些设备可以刚性地或使用铰链关节以有限刚度直接安装到“接地”上。这也可以使用齿轮的指定位移/旋转子节点完成。

请注意，也可以将轴支撑在:

• 柔性外壳
• 刚性外壳
• 接地

这也可以使用铰链关节完成，它可以是刚性的或具有有限的刚度。

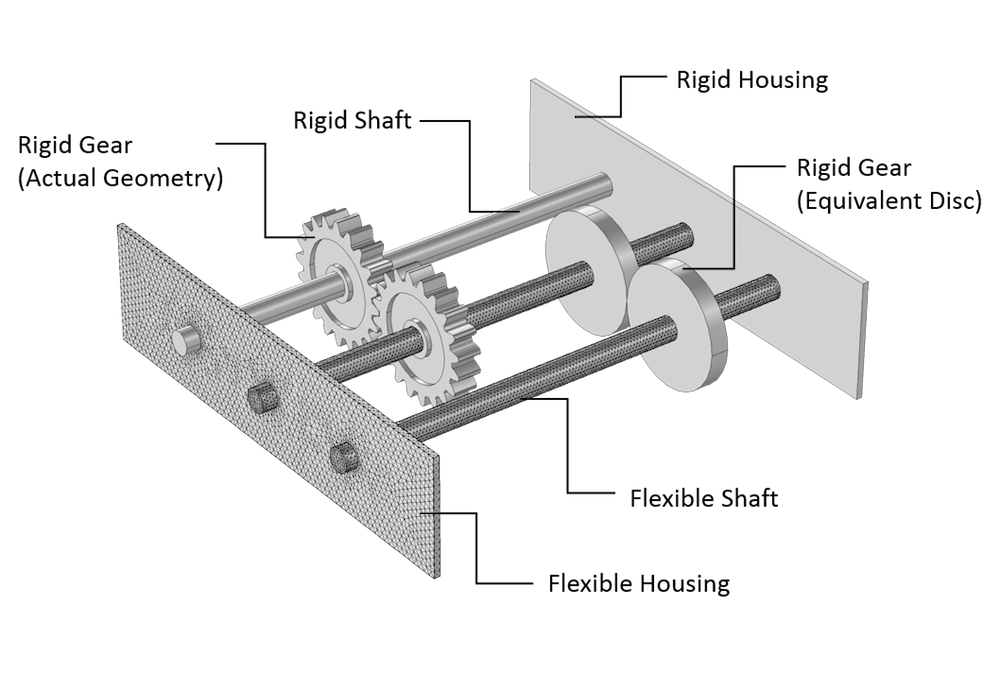
图中显示了具有实际几何形状的齿轮以及通过等效圆盘建模的齿轮。还描述了齿轮和轴的不同安装方法。

连接两个齿轮

你可以使用齿轮副 节点连接你在模型中定义的不同类型的齿轮。该节点可以连接直齿轮、斜齿轮和锥齿轮。你还可以针对特定情况使用蜗杆蜗轮副 和 齿轮齿条副 节点。这些节点以在接触点沿作用线没有相对运动的方式连接两个齿轮。两个齿轮的剩余位移和旋转相互独立。

每个齿轮副 节点增加了两个自由度：

• 轮绕齿轮轴旋转
• 小齿轮绕齿轮轴旋转

为了连接两个齿轮，齿轮副 节点添加了以下约束:

• 旋转约束：使用齿轮比建立轮和小齿轮旋转之间的连接。齿轮比定义为齿轮与小齿轮的角速度之比，也可取小齿轮与齿轮的齿数之比求得。约束还包括齿轮弹性、传动误差和齿隙的影响。
• 接触点约束：这可确保接触点沿动作线没有相对运动。
• 独特三重约束：确保两个齿轮的坐标系仍然唯一且定义明确。它对行星齿轮特别有用。

对于线接触模型，添加了另一个约束以限制关于连接两个齿轮中心的线的相对旋转。如果包含摩擦力，则使用接触力获得摩擦力，该接触力计算为接触点约束的反作用力。然后将这些摩擦力施加在齿轮上，平面内方向垂直于作用线。

正确齿啮合的兼容性标准

在齿轮副节点中，您可以选择模型中定义的任意两个齿轮。但为了实现正确的齿啮合，一组齿轮必须满足以下兼容性标准:

• 两个齿轮的法向模数必须相同
• 两个齿轮的压力角必须相同
• 对于平行轴斜齿轮，螺旋角之和必须为零
• 对于交错轴斜齿轮，螺旋角之和必须为非零

在软件中，所有这些检查将自动执行，如果所选的两个齿轮不兼容，则在方程编译期间发出错误消息。

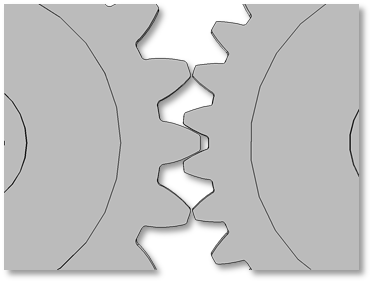
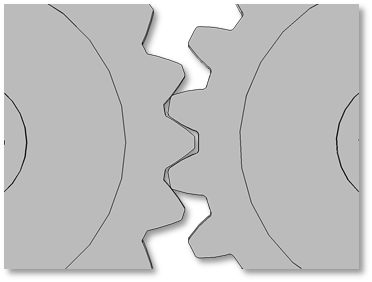
不兼容齿轮啮合的例子。在左边的图中，齿轮有不同的模数。在右边的图中，齿轮有不同的压力角。

定义齿轮坐标系

每个齿轮的坐标系是使用齿轮轴和两个齿轮的旋转中心定义的。坐标系的第一个轴是齿轮轴本身。第二个轴是从旋转中心指向接触点的方向。第三个轴垂直于包含前两个轴的平面。这个坐标系附加到齿轮上，并随着齿轮方向的变化而变化。但是请注意，它不会随着齿轮绕其自身轴的旋转而旋转。

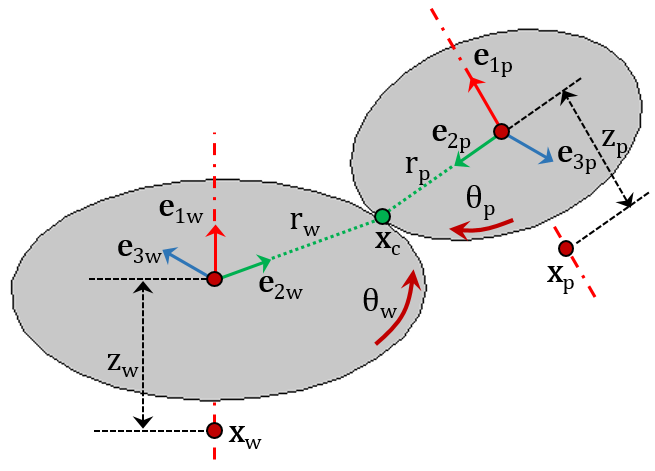
图示显示由一个齿轮副连接的两个齿轮的坐标系和其他参数。

这些量由上图所示的齿轮副表示:

• 齿轮({e_{1 w}e_{2 w}e_{3 w}｝)及小齿轮({e_1便士e_{2 p}e_{3 p}｝）坐标系
• 齿轮(X_w)及小齿轮(X_p）转动中心
• 齿轮(r_w)及小齿轮(r_p）节圆半径
• 齿轮(z_w)及小齿轮(z_p）轴向偏移量
• 齿轮(θ_w)及小齿轮(θ_p)绕各自的轴旋转

齿轮坐标系和作用线

使用齿角矩阵旋转齿轮坐标系，为两个齿轮定义齿轮齿坐标系。该矩阵是使用螺旋角和锥角构建的。

同时，作用线定义为节圆上接触点处齿轮齿面的法线方向。这是力从一个齿轮传递到另一个齿轮的方向。它是通过以使齿坐标系（齿轮切线）第三轴绕齿坐标系第一轴旋转压力角( α )来定义的。根据驱动齿轮的方向，齿轮切线可以顺时针或逆时针旋转。

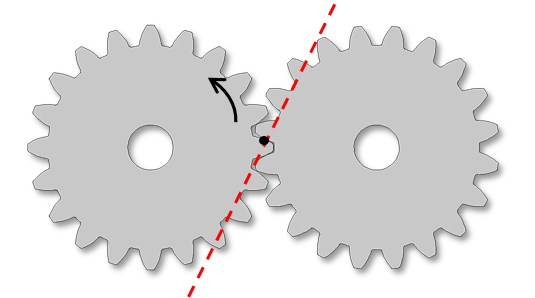
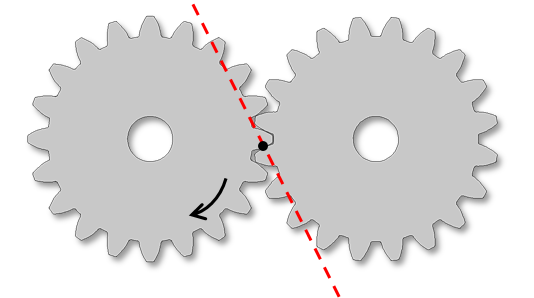
两个图形描绘的作用线和驱动齿轮的旋转方向。根据驱动齿轮和切线在顺时针方向(左)和逆时针方向(右) 旋转的事实定义的作用线。

齿轮接触模型

两个齿轮之间的接触是通过解析建立的方程进行建模的。这些方法独立于有限元网格，因此比基于网格的接触方法更快、更稳健。要计算接触力和力矩，您可以选择以下两种方法:

1. 使用弱形式约束：该方法采用弱形式实现接触点约束，该约束的拉格朗日乘子为接触力。这种方法是准确的，但它使用了一个额外变量的拉格朗日乘子，并需要适当的缩放，才能获得良好的收敛性。
2. 使用罚方法: 这里，使用罚方法实现约束，罚力表示接触力。这种方法不需要任何额外的变量，但是必须为罚因子选择一个合适的值。

每个齿轮上的接触点通过旋转中心、旋转中心的位移矢量、接触点从齿轮中心的偏移、节圆半径和锥角来定义。根据两个齿轮的方向，不同的齿轮副可以归类为以下两种配置之一:

1. 平行的或相交的(即正齿轮、斜齿轮和锥齿轮)
2. 既不平行也不相交(即交叉斜齿轮和蜗轮)

对于一个平行或相交配置，接触点从小齿轮中心的偏移量是输入的，接触点从齿轮中心的偏移量是自动计算的。接触模型可以选择为：

• 点接触，适用于薄齿轮
• 线接触，适用于厚齿轮

对于既不平行也不相交配置，会自动计算与小齿轮以及齿轮中心的接触点偏移量。这样做的原因是始终存在点接触，并且可以唯一确定接触点。

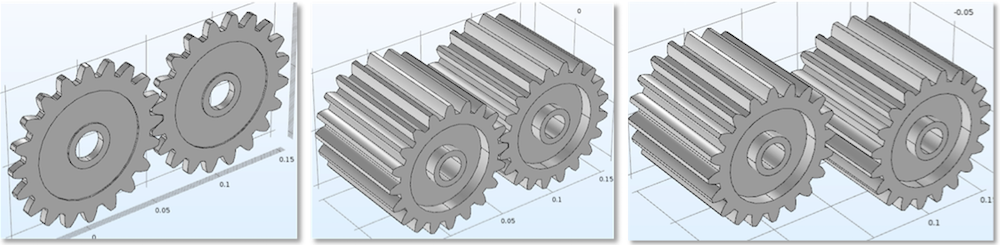
从左到右:薄齿轮(点接触模型)，厚齿轮(线接触模型)和具有轴向偏移的厚齿轮。

不同齿轮副的例子

现在，我们已经进一步详细地探讨了齿轮以及如何连接它们，接下来我们看看根据其配置分类的齿轮副的各种示例。您可以使用多个齿轮副来模拟复杂的平行齿轮系和行星齿轮系。

平行轴配置的一些示例如下:

• 外部直齿轮
• 外斜齿轮(平行)
• 内直齿轮
• 内斜齿轮(平行)

同时，斜齿轮提供了一个交错轴配置的例子。

一组带外齿轮啮合的直齿轮和平行斜齿轮。

一组直齿轮，一个与内齿轮啮合，另一个与外齿轮啮合，以及一组锥齿轮。

一些交叉(既不平行也不相交)轴配置的例子如下:

• 外斜齿轮(交叉)
• 蜗轮和齿轮

一组带有外齿轮啮合和蜗轮的交叉斜齿轮。

带有直齿轮啮合的齿条和小齿轮。

理解和处理齿轮建模的重要元素

在进行齿轮建模时，需要考虑许多重要因素来优化您的仿真结果。正如我们今天在这里展示的，COMSOL Multiphysics 中的齿轮建模的新特征和功能帮助你解决这些元素，为你提供有关如何改进齿轮设计的更有用的见解。

在我们的齿轮建模系列的下一篇博客文章中，我们将讨论如何在你的齿轮对(即，齿轮啮合弹性、齿隙、传动误差和摩擦) 上使用高级功能，来进行真实度要求更高的模拟。我们还将向你展示这些参数如何影响系统的动力学。敬请继续关注!