理论介绍——什么是规范固定

规范固定是计算电磁学中最有趣的主题之一。本篇博文，我们将介绍什么是规范固定及其背景知识，并讨论什么时候以及怎样在 COMSOL Multiphysics® 软件中使用它。

亥姆霍兹定理

COMSOL Multiphysics^® 中的电磁场物理接口都旨在为麦克斯韦方程组提供解，那么它们之间有什么区别？首先，为什么需要多个“麦克斯韦接口”？

为了回答这个问题，并解决一些常见的误区，让我们先退一步并回看一下矢量场的数学概念，因为麦克斯韦方程组处理的矢量场是时间和空间的函数，即 \textbf{E}, \textbf{D}, \textbf{H}, 和 \textbf{B}。

亥姆霍兹定理是分析麦克斯韦方程组的起点，也称为矢量计算的基本定理。它指出，任何矢量场 \textbf{F} 都可以解耦为无旋度部分和无散度部分。通过了解所有 \nabla \times \textbf{F} 和 \nabla \cdot \textbf{F}，以及对于截断的域和适当的边界条件，可以唯一确定矢量场。

当然，对 \textbf{F} 进行解析解可能比较困难，甚至不可能完成，而且数值计算也不容易。

麦克斯韦方程

麦克斯韦方程的微分形式可以表示为：

其中，\textbf{E} 和 \textbf{H}分别是电场强度和磁场强度；\textbf{D} 和 \textbf{B} 分别是电位移场和磁通密度;\rho 和 \textbf{J}分别是电荷密度和传导电流密度。

此外， 材料定律确定了 \textbf{E} 到 \textbf{D} 和 \textbf{H}到 \textbf{B}的唯一关系。根据亥姆霍兹定理，很显然，这些方程（具有足够的边界条件）提供了唯一的矢量场 \textbf{E}, \textbf{D}, \textbf{H}, 和 \textbf{B}。同样地，对于 \nabla \times \textbf{H} 和 \nabla \cdot \textbf{H}，\nabla \times \textbf{E} 和 \nabla \cdot \textbf{E} 也被规定。

势简介

通常，使用标势和矢势来重新表示麦克斯韦方程组很方便，但这些不一定是唯一的，需要使用亥姆霍兹定理来解析，接下来我们将进行讨论。

在静力学及静磁场中，\nabla \times \textbf{E} = \textbf{0} ；在不存在电流的情况下，\nabla \times \textbf{H} = \textbf{0}。

在这种情况下，我们可以使用标势（当\nabla \times (\nabla f)= \textbf{0}，对于任何标量函数f) ）分别表示\textbf{E} 和 \textbf{H}，即：

此外，在没有自由电荷存在的情况下，\nabla \cdot \textbf{B} = 0和\nabla \cdot \textbf{D} = 0始终成立。

然后，我们可以使用矢势 （对于任何矢量场\textbf{F}) ， (\nabla \cdot (\nabla \times \textbf{F}) = 0）分别表示 \textbf{B} 和 \textbf{D}（没有空间电荷密度时）的无散度部分：

与直接使用场分量或矢势表示相比，在数值表达中使用标势很有优势，因为它可以将未知数减少3倍，并且将计算载荷（对于直接求解器而言）降低了一个数量级。从理论的角度来看，它也是有优势的，因为通常使用标势更容易找到解析解。

但是，在电磁学中，一个最大的挑战和最普遍的误解是，大学时学习的矢量计算几乎总是以使用标势表示的无旋度场分析的特殊情况开始的。按照“第一印象”的原则，学生在毕业后面对现实问题时，常常会忘记对需要考虑旋度非零的情况进行更复杂分析。这篇博客文章可能有助于填补这一空白。

势和规范转换的唯一性

许多关于势使用的陷阱和困难都与势的唯一性有关。如前所述，物理场 \textbf{E}, \textbf{D}, \textbf{H}, 和 \textbf{B} 都可通过麦克斯韦方程组获得唯一解。但是，当把标势和矢势代入麦克斯韦方程组时，这些势通常具有无限多个解，除非添加了额外的方程或条件。

在下文中，假设使用电标势 V 和磁矢势 \textbf{A} 来表示麦克斯韦方程组的解，并且 \textbf{E} 、 \textbf{D}、 \textbf{H} 和\textbf{B}之间线性相关（材料定律）。实际上，我们可以自由地使用任何一个势的组合（(V, V_m, \textbf{A}, 和 \textbf{F}）来分别表示 \textbf{E}和\textbf{H}的非零旋度，以及麦克斯韦方程组所要求的非零散度\textbf{D}。

首先，对于电标势 V，在静电场中， \nabla \times \textbf{E} = \textbf{0}，因为法拉第定律中没有感应电场。然后，我们可以假设 \textbf{E} = – \nabla V。但是，V的定义并不唯一，因为

这里，C是常数，将产生相同的静电场。

因此，电标势需要至少一个额外的条件来固定其一般水平，以获得唯一解。通常，这由边界条件（接地或施加的电势）给定。

对于磁矢势 \textbf{A}，情况会更复杂。

可以看到，我们可以将任一度标量函数的梯度 \psi添加 到 \textbf{A}。

由于存在\nabla \times (\nabla \psi)= \textbf{0}，因此将得到同一个（唯一的）\textbf{B}。

通过标量函数的梯度移动矢势称为规范变换。根据亥姆霍兹定理，该规范不确定性是由于仅指定了的旋度 \textbf{A}。我们还需要指定其散度，以得到一个唯一的矢势 \textbf{A} ，这可以通过添加一个常数矢量 \textbf{C}实现。后者通常由边界条件确定。对于 \nabla \cdot \textbf{A}，常见的选择是库仑规范（Coulomb gauge）：

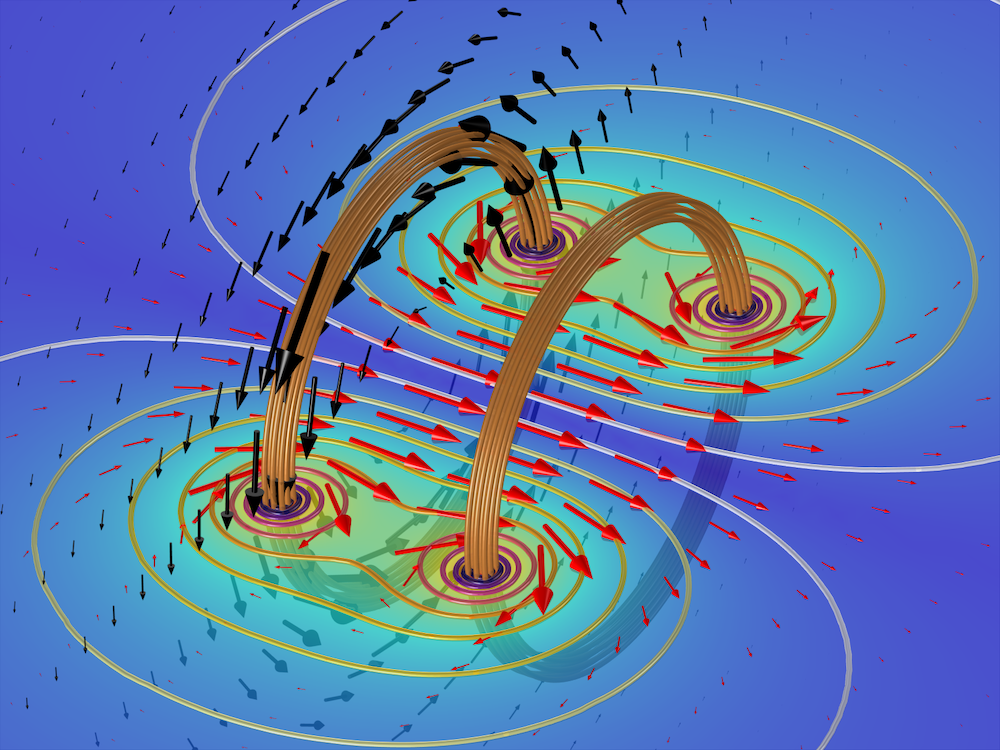
一个静态亥姆霍兹线圈中，计算得到的 \textbf{A}场（黑色箭头和等值线表示幅值）和 \textbf{B}场（红色箭头和切面表示幅值）。每个绕组由 10 匝铜导线组成，这些铜绕组具有相等的电流，且与 \textbf{A}场的流动方向平行。 \textbf{A} 场用于计算库仑规范  \nabla \cdot \textbf{A} = 0.

电磁学中的势转换

到目前为止，我们已经假设了静态条件且材料没有运动，因此没有感应电场，也没有位移电流密度。在这些条件下，电场和磁场是单向耦合的。静电场驱动直流传导电流密度，进而产生磁场。

现在，放宽时间导数为零的条件，法拉第定律（Faraday’s law）表示为

之后，插入\textbf{B} = \nabla \times \textbf{A}：

如果我们定义以下条件，则满足法拉第定律：

但是，重复上一节中的规范转换练习，我们发现，为了不更改的\textbf{E}定义，不仅必须转换\textbf{A} 而且还必须转换 V;即

使

那么，\textbf{A} 和V都取决于规范的选择，并有助于电场 \textbf{E} 独立于 \psi 。

另外值得注意的是，在麦克斯韦-安培定律中，电场通过传导和位移电流密度项 – \sigma\textbf{E} + \frac{\partial\textbf{D}}{\partial t}影响磁场。就像在法拉第定律中， – \frac{\partial\textbf{B}}{\partial t} 如何作为\nabla \times \textbf{E} 的源项。因此，动态电场和磁场是双向耦合的（也称为全耦合电磁或“全麦克斯韦”公式）。

另一个非常重要的结果是，电势仅对电场 \textbf{E} 产生部分且依赖规范的贡献。这意味着对于电压U，只能根据电场的线积分项来定义：

因此，对于经常使用“势差”概念的无旋电场分析和电路分析，“势差”概念的使用通常不适用。此外，在电动力学中，测得的电压取决于积分路径 L 的选择；例如，耦合线圈的定位。

选择规范的方法有很多种。库伦规范会产生一个电势，该电势立即对电荷密度的变化做出反应（甚至很远），而磁矢势则表现出有限的传播速度。这可能看起来很奇怪，并且可能与相对论相悖，但是请记住，势不能直接测量。只有电场\textbf{E}可通过它对电荷的影响来测量，而且根据定义，它且不受规范选择的影响。

亥姆霍兹矢量方程

一种让人特别感兴趣的规范是当我们选择使得电势消失，即：

该规范仅对动态公式有效，因为在静态极限下，它的值会退化,使 \textbf{E} 未定义。它被用于矢量亥姆霍兹方程，该方程用于 RF 模块 的 频域和电磁波接口，以及AC/DC 模块中的频域和磁场 接口。在第一种情况下，因变量是\textbf{E}；在第二种情况下，因变量是 \textbf{A}。从数学的角度来看，在频域中它不产生任何显著的差异，因为在频域中应用了时谐的规定\textbf{E}(t,\textbf{r}) = Re(\textbf{E}(\textbf{r})e^{j\omega t})：

因此，\textbf{E} 和\textbf{A}的差异仅在于一个全局因子 – j\omega。

查看磁场接口，频域方程可表示为：

在频率足够低的情况下，包含omega的项在数值上消失，该方程变得与静磁公式相同：

然后，当电磁部分（与感应电场 \textbf{E} = – j\omega\textbf{A}有关） 在数值上变得无关紧要时，规范V 也会随着的消失而消失。因此，对\nabla \cdot \textbf{A} 的固定， \textbf{A}在数值上也变得微不足道，并且也不再唯一确定。

所有这些可以看作是电磁耦合在静态极限内丢失的结果。因此，需要一个单独的电场方程（基于不再消失的V）。

这意味着亥姆霍兹矢量方程仅限于应用在感应传导或位移电流密度在数值上很重要的情况。

A-V公式

在低频下，对于 \textbf{A} 和 V，推荐使用求解和的公式，因为这允许势在静态极限下优美地解耦（分离但耦合的方程求解 \textbf{A} 和 V）。代价是您必须采取外在措施来处理规范不确定性。也就是说，对 \nabla \cdot \textbf{A} 指定一个条件，AC / DC 模块中的磁场和电场接口可同时求解 \textbf{A} 和 V。

结语

至此，我们已经研究了将亥姆霍兹定理应用于麦克斯韦方程组，以及用标势和矢势表示物理场\textbf{E}, \textbf{D}, \textbf{H}, 和 \textbf{B}的结果。结论如下：

• 只有矢量场的旋度和散度都已知，矢量场才能唯一确定；
• \textbf{E}, \textbf{D}, \textbf{H}, 和 \textbf{B} 通过麦克斯韦方程组和材料定律唯一确定；
• 在麦克斯韦方程组中引入标势 V 和矢势 \textbf{A}是有用的，但除非指定了 \nabla \cdot \textbf{A} ，并提供了V的参考水平，否则势不唯一确定；
• 施加在 \nabla \cdot \textbf{A} 上的条件和 V 的一致定义之间存在动态关系（规范），这决定了电场 \textbf{E} 独立于所选规范；
• 势 \textbf{A} 和 V 都对 \textbf{E} 有贡献，因此电压U 只能用依赖路径的线积分 U=\int_L{\textbf{E}\cdot}d\textbf{l} 测量。
• 特定的规范 V=0 可导出 \textbf{A} 或 \textbf{E} 的亥姆霍兹矢量方程，这对于电磁波传播、感应涡流以及具有足够强电磁耦合的其他效应的模拟非常有用。
  • 然而，低频下它在数值上失效，需要一个同时使用\textbf{A} 和 V的公式。

在本系列的下一个博客中，我们将讨论如何在静磁学中实施一个外在的特定规范以及何时在频域内求解 \textbf{A} 和 V 。另外，我们还将讨论电荷守恒，即连续性方程内置在麦克斯韦方程组中，以及源电流为螺旋状时，它如何限制了解的存在。事实证明，后者是在静磁学和低频电磁学中成功进行数值模拟的关键因素。敬请关注！