磁场电磁学简介
什么是电磁学?
电磁学属于工程领域,传统上来说,人们是通过分属于众多子领域(例如静电学或光学)的专业术语和设备来逐渐了解电磁学的。静电设置中使用的设备(如电容器)和光学器件(如光纤)几乎没有共同之处,尽管它们的特性有很大的差异,但所有这些应用基本上都用麦克斯韦方程组进行描述。在工程应用中,这些方程几乎总是需要使用其他定律作为补充,通过这些定律来描述电磁场与介质相互作用的方式。下表列出了麦克斯韦方程组的微分形式:
| 方程名称 | 微分形式 |
|---|---|
| 麦克斯韦-安培定律 | |
| 法拉第定律 | |
| 高斯定律 | |
| 高斯磁定律 |
我们将在以下各个章节中介绍这些方程的含义。
在实际应用中,我们很少需要考虑可能发生的所有电磁现象。相反,我们往往是通过分析各种特殊情况来获取对电磁学更实际的理解,其中包括静电、恒定电流、静磁、准静态交流电、电感现象、微波工程和光学。
静电学
静电学是电磁学的一个子领域,研究静(非运动)电荷引起的电场。静电学是麦克斯韦方程组的近似表述,只能用于描述完全以介电常数(有时称为电容率)表征的绝缘材料或电介质材料。在执行静电分析时,我们首先从分析中去除所有导电材料(通常是金属),然后从电介质材料的角度将金属表面视为外部边界。静电分析的典型输入和输出汇总如下:
| 输入 | 符号 | 几何位置 |
|---|---|---|
| 相对介电常数 | 体 | |
| 电位 | 导电边界 | |
| 表面电荷密度 | 边界 | |
| 体电荷密度 | 体 | |
| 极化 | 体 | |
| 输出 | 符号 | 几何位置 |
| 电位 | 体 | |
| 悬浮电位 | 导电边界 | |
| 表面电荷密度 | 导电边界 | |
| 电场 | 体 | |
| 电位移场 | 体 | |
| 电容矩阵 | 全局 | |
| 静电力 | 全局 |
请注意,在静电分析中,我们将所有电荷都视为静止,因此没有电流输入或输出。在某些情况下,体电荷密度也可以作为分析的输出。

平行板电容器周围整个体的电位和电场横截面视图。图中用填充等值线表示电位,并通过标签表明电位水平。电场显示为具有对数比例的箭头。电位还受到远处周围介质的影响(图中未显示)。
平行板电容器周围整个体的电位和电场横截面视图。图中用填充等值线表示电位,并通过标签表明电位水平。电场显示为具有对数比例的箭头。电位还受到远处周围介质的影响(图中未显示)。
静电分析的典型应用是电容器件和传感器(如触摸屏)的电容计算,以及绝缘体、MEMS 加速度计和 MEMS 陀螺仪的介电强度计算。
恒定电流
恒定电流分析用于计算金属等高导电材料中的恒定电流流动。电子流在电位差的驱动下流过导体,尽管实际上电子的运动方向与电流方向相反,但按照惯例以及由于历史原因,我们通常认为电流是从高电位流向低电位。这一惯例起源于人们发现电子之前。
恒定电流分析中的材料完全用电导率来表征。在执行恒定电流分析时,我们首先从分析中去除所有绝缘材料,然后从导电材料的角度将绝缘表面视为外部边界。
恒定电流分析的典型输入和输出汇总如下:
| 输入 | 符号 | 几何位置 |
|---|---|---|
| 电导率或电阻率 | 体 | |
| 电位 | 边界 | |
| 法向电流密度 | 边界 | |
| 输出 | 符号 | 几何位置 |
| 电位 | 体 | |
| 悬浮电位 | 导电边界 | |
| 法向电流密度 | 边界 | |
| 电场 | 体 | |
| 电流密度 | 体 | |
| 电阻矩阵 | 全局 |

螺旋电感中的电流密度,其中左右边界之间施加了电位差。图中显示电感器内部的电流密度大小值。蓝色和红色分别表示大小的谷值和峰值。箭头显示电流密度的方向。电流趋向于流经最短路径,如该结构内角处的红色区域所示。
螺旋电感中的电流密度,其中左右边界之间施加了电位差。图中显示电感器内部的电流密度大小值。蓝色和红色分别表示大小的谷值和峰值。箭头显示电流密度的方向。电流趋向于流经最短路径,如该结构内角处的红色区域所示。
恒定电流分析的典型应用包括电子元件、电缆、高压系统组件、医疗设备、传感器、岩土分析和腐蚀。
电准静态
电准静态分析是在磁效应可以忽略的情况下,对静电和恒定电流的泛化分析。如果存在时变场,我们就只能将静电的电容效应与恒定电流分析的导电效应结合起来分析。对于静态情况,我们可以将麦克斯韦方程组分为静电和恒定电流两种情况,由于二者表示相互排斥的现象,因此必须选择其一。然而,如果某个物理量随时间变化,如边界上的电压,则总电流为传导电流与位移电流之和。传导电流密度与电导率相关,位移电流密度与介电常数相关。电准静态可以看作是恒定电流方程(包含位移电流产生的额外贡献)的动态形式。对于驱动电流或电压呈正弦变化的时谐分析,场变为复值,其中相角表示传导电流与位移电流之比。
电准静态分析的典型输入和输出汇总如下:
| 输入 | 符号 | 几何位置 |
|---|---|---|
| 电导率或电阻率 | 体 | |
| 相对介电常数 | 体 | |
| 电位 | 边界 | |
| 法向电流密度 | 边界 | |
| 输出 | 符号 | 几何位置 |
| 电位 | 体 | |
| 悬浮电位 | 导电边界 | |
| 法向电流密度 | 边界 | |
| 电场 | 体 | |
| 电流密度 | 体 | |
| 电阻矩阵 | 全局 |

四极质谱仪中的离子轨迹。这种类型的质谱仪利用静电位和时谐电位的巧妙组合对粒子进行分类。通过调节谐波频率(本例为 4 MHz)以及静电场和谐波场的强度,只有一定质量的粒子能通过该设备进行传输。
四极质谱仪中的离子轨迹。这种类型的质谱仪利用静电位和时谐电位的巧妙组合对粒子进行分类。通过调节谐波频率(本例为 4 MHz)以及静电场和谐波场的强度,只有一定质量的粒子能通过该设备进行传输。
电准静态分析的典型应用包括医疗设备、传感器,岩土分析和质谱仪。
要了解有关电准静态理论的更多信息,请参阅电准静态理论。
静磁学
静磁学可以看作是恒定电流在磁场中的泛化表示,当我们想要了解导体周围的磁场信息时,就需要研究这一领域。这种情况下,恒定电流分析有时用作预处理步骤,产生的电流用作后续静磁分析的输入。例如,电磁体的分析就是这种情况。用于执行静磁分析的基本材料属性是相对磁导率。非线性静磁分析可能需要更广泛的材料关系,比如磁场与磁通密度之间的函数关系:B-H 曲线。在许多情况下,静磁分析的最终目的是计算线圈系统的互感和自感,或磁性元件系统中的力和力矩。
永磁体分析是静磁分析中的一种重要的特殊情况。在这种情况下,磁场的源是永磁化,而非电流。对于这类情况,磁通强度和方向以及力是非常重要的分析结果。
静磁分析的典型输入和输出汇总如下:
| 输入 | 符号 | 几何位置 |
|---|---|---|
| 电导率或电阻率 | 体 | |
| 相对磁导率 | 体 | |
| B-H 曲线 | 体 | |
| 线圈中的电流密度 | 体 | |
| 磁场 | 边界 | |
| 表面和边上的电流密度 | 边界 | |
| 输出 | 符号 | 几何位置 |
| 磁场 | 体 | |
| 磁通量 | 体 | |
| 电感矩阵 | 全局 | |
| 磁力 | 全局 |
静磁分析的典型应用包括电磁体、永磁体、线圈、电感器和螺线管。
要了解有关静磁学理论的更多信息,请参阅静磁学理论。
磁准静态
我们可以根据麦克斯韦方程组得到一个推论,即电流和电荷随时间的变化与电磁场的变化不同步。场的变化总是滞后于源的变化,反映了电磁波的传播速度有限。我们假设这一效应可以忽略不计,通过分析“每个瞬间的稳定电流”,就可以得到电磁场。只要时间变化足够小,并且研究的几何结构远小于波长,就可以使用这种低频近似。根据经验,当设备的特征尺寸(电尺寸)小于波长的 10%% 时,我们就可以使用准静态近似。
磁准静态近似对于理解 50 Hz 或 60 Hz 电网中的电磁部件非常重要。这类分析对于更高频的情况同样起着非常重要的作用,有时还可与全波电磁分析相结合,用于评估电磁干扰现象。
在分析线性材料属性以及正弦电流和正弦场时,我们采用时谐研究。这类研究每次可以分析部件在一个频率下的情况,并能够一次性捕获部件在所有时间的完整特性,因此非常高效。对于具有非线性材料或波形扭曲的部件,需要进行全瞬态分析,耗费的计算时间较长。
磁准静态元件的激励通过在所研究域的边界上施加时变电压或电流来实现,也可以通过施加体积线圈电流实现。此类激励方法仅在低频工况下有效。在频率较高时,有限光速引起的辐射损耗和影响变得非常重要,此时可能需要进行高频分析。
磁准静态分析的典型输入和输出汇总如下:
| 输入 | 符号 | 几何位置 |
|---|---|---|
| 电导率或电阻率 | 体 | |
| 相对介电常数 | 体 | |
| 相对磁导率 | 体 | |
| B-H 曲线 | 体 | |
| 线圈中的电流密度 | 体 | |
| 磁场 | 边界 | |
| 表面和边上的电流密度 | 边界 | |
| 输出 | 符号 | 几何位置 |
| 磁场 | 体 | |
| 磁通量 | 体 | |
| 阻抗矩阵 | 全局 |
磁准静态的典型应用包括电缆、电力线、变压器、发电机、电机、电抗镇流器、电感器和电容器。
电磁波
詹姆斯·克拉克·麦克斯韦通过在安培定律中添加一个位移电流项以扩大其适用性,发现了现在称为麦克斯韦-安培定律的方程。通过将该定律与法拉第定律相结合,他发现了可以用电磁波方程表示的电磁现象的波动性。电磁波方程有多种公式,以下是一个电场相关的公式例子:
类似地,磁场公式为:
麦克斯韦据此得出了多项结论,其中一个重要结论是:光速是所有电磁现象的普遍速度。根据下式,光速与介电常数和磁导率有关:
用于分析电磁现象的连续介质方法已经证实在许多应用中获得了成功,但仍存在一定的局限性。在微观结构中,物质的离散性质起着重要的作用,在分析这种结构时,我们需要采用量子力学方法。对于甚高频,可以更有效地将电磁波作为射线进行分析;对于高于甚高频的情况,在模拟单个光子时,还必须为它们与物质之间的电离作用进行建模。
为了确定合适的电磁分析方法,我们必须考虑物体特征尺寸与波长之间的相对关系。下图对这一关系进行了概述。
在分析用于引导或辐射电磁波的装置时,电磁场的波动性是非常重要的因素。这类装置包括同轴电缆、微波电路、波导和天线等。
在高频下,有限光速的影响变得至关重要,电压等物理量在边界段上不再恒定,因此不能直接用于激励装置。此时,我们改为在端口或端口边界上使用场模式,这是与麦克斯韦方程组相容的特征模态。只要使用正确,这些类型的边界条件就能够在很少的损耗下激励结构,从而在理想条件下捕捉结构的固有性能。
有时,使用工程方法会非常方便,这种方法用电压和电流激励表示来自相邻电路的馈电。这些激励可以同一些周密的方案结合使用,从而转换为兼容的端口激励。在这种情况下,能量损耗不可避免,这些损耗可能表示实际的设备馈电损耗或人工建模损耗,或两者兼有。类似地,监听端口用来以一种与麦克斯韦方程组一致的方式传输出射能量。传输和反射的能量作为散射参数或 S 参数进行计算,这些参数表示通过各个端口的能量输入和输出。
电磁波分析的典型输入和输出汇总如下:
| 输入 | 符号 | 几何位置 |
|---|---|---|
| 电导率或电阻率 | 体 | |
| 相对介电常数 | 体 | |
| 相对磁导率 | 体 | |
| 端口 |
边界 | |
| 端口 |
边界 | |
| 馈电线路电压或电流 | 边界 | |
| 输出 | 符号 | 几何位置 |
| 电场 | 体 | |
| 磁场 | 体 | |
| 阻抗矩阵 | 全局 | |
| 导纳矩阵 | 全局 | |
| S 参数矩阵 | 全局 | |
| 天线参数 | 无约定 | 全局 |
要了解有关电磁波理论的更多信息,请参阅电磁波理论。
电磁热
焦耳热
电流在流经电阻时,电能转化为热能的过程称为焦耳热(也称电阻加热或欧姆加热)。
具体来说,当电流通过有限电导率的固体或液体时,材料中的电阻损耗会使电能转化为热能,其中的传导电子通过碰撞的方式将能量传递给导体的原子,在微小尺度上产生热量。
在某些情况下,电气设备的设计需要使用焦耳热效应;但在另一些情况下,我们又希望避免这种效应。一些依赖于焦耳热的应用包括电热板(直接作用),以及用于流体控制的微型阀(间接作用,通过热膨胀实现)。
在设计过程中,我们可以根据需要采取相应的措施,减小焦耳热效应。电气系统元件(如电子产品中的导体、电暖气、电线和保险丝等)的设计尤其如此,这些结构在受热时会老化甚至熔化。为了防止这些元件和设备过热,工程师们常常在设计中采用对流冷却。
下面是以焦耳热方式在加热回路中引发机械应力的一个例子。在电路上施加电压后,玻璃板上的导电层会产生焦耳热;这反过来又会影响电路的结构完整性,并使玻璃板发生弯曲。
焦耳热分析的典型输入和输出汇总如下:
| 输入 | 符号 | 几何位置 |
|---|---|---|
| 电导率或电阻率 | 体 | |
| 电位 | 边界 | |
| 法向电流密度 | 边界 | |
| 导热系数 | 体 | |
| 热容 | 体 | |
| 质量密度 | 体 | |
| 温度 | 边界 | |
| 热通量 | 边界 | |
| 输出 | 符号 | 几何位置 |
| 电位 | 体 | |
| 电流密度 | 体 | |
| 功率损耗 | 体 | |
| 温度 | 体 | |
| 热通量 | 体 |
感应加热
感应加热与焦耳热效应非常相似,但有一个重要的不同之处:对材料进行加热的电流是电磁感应产生的,这是一种非接触式(或非局部)的加热过程。
通过在感应线圈上施加高频交流电,可以产生一个时变磁场。将被加热的材料(称为工件)放置在磁场内,但不接触线圈。请注意,并非所有材料都可以实现感应加热;这种方法只适用于电导率较高的材料(如铜、金、铝等)。在交变电磁场的感应作用下,工件中会产生涡流,导致电阻损耗,从而达到对材料进行加热的目的。
更进一步来说,高频电流会引起集肤效应,迫使交流电以薄层的形式流向工件表面,从而使导体的电阻增加,最终使加热效果得到大幅提升。
与其他材料相比,黑色金属更容易实现感应加热。原因在于,这类金属的高磁导率会增强感应涡流和集肤效应;不仅如此,还有另外一种加热机制在发挥作用。这种材料的铁晶体被交变磁场反复磁化和消磁,导致磁畴快速来回翻转,引起磁滞损耗,进而产生更多热量。
由此可见,在感应加热过程中,工件和感应线圈之间不发生物理接触。因为这个原因,这种方法可被用于对清洁度要求极高的工艺,比如半导体制造。
不仅如此,由于热量是在工件内部 产生,而不是先在其他位置产生再作用于工件,因此这种加热方法非常高效。换句话说,通过感应加热,我们可以避免用于电连接的表面产生热损耗,从而提高整体加热效率。
感应加热过程涉及两种不同类型的物理现象:电磁和传热。由于某些材料属性与温度相关,这意味着它们在受热时会发生改变。对于这种情况,您可以考虑将这两种物理现象进行耦合分析。
电磁炉便是利用感应加热的一种创新设计。在这一设计中,线圈放置在炉面下方,其电磁场作用在金属锅上。由于这种方式只能对高导电材料进行加热,因此金属锅会受热升温;然而,如果您将手放在炉面上,却并不会感到热。
在半导体工业中,人们也利用这一过程来加热硅材料,其他应用还包括密封、热处理和焊接。
尽管众多的产品和工艺都离不开感应加热技术带来的优势,然而在其中一种应用中,加热会造成电能的浪费。对于变压器而言,设计上很重要的一点是不 让涡流通过磁芯内部。如果变压器的磁芯被涡流加热,那么不仅会浪费电能,还有可能导致更多问题,比如结构损伤。
感应加热分析的典型输入和输出汇总如下:
| 输入 | 符号 | 几何位置 |
|---|---|---|
| 电导率或电阻率 | 体 | |
| 相对磁导率 | 体 | |
| 线圈电流 | 体 | |
| 导热系数 | 体 | |
| 热容 | 体 | |
| 质量密度 | 体 | |
| 温度 | 边界 | |
| 热通量 | 边界 | |
| 输出 | 符号 | 几何位置 |
| 电场 | 体 | |
| 磁通量 | 体 | |
| 感应电流密度 | 体 | |
| 功率损耗 | 体 | |
| 温度 | 体 | |
| 热通量 | 体 |
微波加热
微波加热是一种同时涉及电磁波和传热的多物理场现象。任何暴露在电磁辐射中的材料都会被加热,迅速变化的电场和磁场可以产生四种热源:任何作用于导电材料的电场都会引起电流流动;此外,时变电场会促使偶极分子(比如水)发生振荡;作用于导电材料的时变磁场也会引起电流流动;不仅如此,某些类型的磁性材料还可能发生磁滞损耗。
微波炉是微波加热的一个典型应用示例。当我们将食物放进微波炉并按下“启动”按钮后,电磁波就会以 2.45 GHz 的频率在微波炉内振荡。这些电磁场与食物相互作用,导致热量的产生和温度的升高。
微波加热的效率取决于材料的性能。举例来说,如果在微波炉中放置多种水分含量不同的食物,那么它们会以不同的速率加热。餐具中的食物可能出现这样的情况:一部分食物已经很烫了,而其余部分却还是冷的。除此之外,食物之间的相对位置也会影响微波炉中的电磁场。这就是为什么大多数微波炉中都带有转盘,通过旋转食物来促进均匀加热。
另一个利用微波加热效应的应用是癌症治疗,具体地说是肿瘤热疗。这种癌症治疗方式是对肿瘤组织进行局部加热,而不损伤周围的健康组织。在微波凝固治疗中,医生将一根很细的微波天线直接插入肿瘤,通过微波将其加热,形成一个凝固区,杀死其中的癌细胞。这种治疗方法需要精确地控制空间分布和加热功率。温度传感器不仅要求做到设计精良,而且摆放位置也必须经过周密细致的考虑,才能避免损伤健康组织。
微波加热分析的典型输入和输出汇总如下:
| 输入 | 符号 | 几何位置 |
|---|---|---|
| 电导率或电阻率 | 体 | |
| 相对磁导率 | 体 | |
| 相对介电常数 | 体 | |
| 端口 |
边界 | |
| 馈电线路电压或电流 | 边界 | |
| 导热系数 | 体 | |
| 热容 | 体 | |
| 质量密度 | 体 | |
| 温度 | 边界 | |
| 热通量 | 边界 | |
| 输出 | 符号 | 几何位置 |
| 电场 | 体 | |
| 磁场 | 体 | |
| 感应电流密度 | 体 | |
| 功率损耗 | 体 | |
| 温度 | 体 | |
| 热通量 | 体 |
电磁力
电磁力可以根据其所属的电磁学子领域进行分类。虽然所有电磁学领域的基本电磁力相同,但它们的特征和计算方法却完全不同。下表汇总了最重要的几种电磁力类型:
| 力 | 子领域 | 主要作用于 | 净力计算方式 |
|---|---|---|---|
| 静电力 | 静电学 | 边界 | 在边界上积分 |
| 介电泳力 | 静电学和电准静态 | 粒子 | 解析式 |
| 静磁力 | 静磁学 | 边界 | 在边界上积分 |
| 洛伦兹力 | 磁准静态 | 体 | 在体积上积分 |
| 辐射压力 | 电磁波 | 边界 | 在边界上积分 |
电磁力广泛用于各种工业设备,包括电磁电机和发电机、电磁铁、继电器、电磁阀、断路器、柱塞和接触器。
电磁力的重要性不仅仅体现在固体材料中。举例来说,在使用感应炉加工金属时,由于熔融金属通常具有较高的导电性,因此了解电磁力非常有必要。磁学和流体流动相结合的领域称为磁流体动力学。

许多工业应用都离不开线性运动,线性电磁执行器在其中起到了不可或缺的作用,其用途包括打开或关闭,推动或拉动载荷等。
许多工业应用都离不开线性运动,线性电磁执行器在其中起到了不可或缺的作用,其用途包括打开或关闭,推动或拉动载荷等。
静磁力
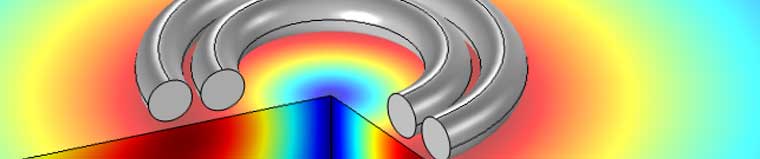
静磁力可以说是人们日常生活中最常见的电磁力,我们身边的永磁体无处不在,冰箱磁贴、各式包袋和钱包的锁扣、电源适配器和笔记本电脑键盘的磁性连接器等,到处都是永磁体的身影。马蹄形磁铁是永磁体的一个经典例子,如下图所示。其中,磁力表现为表面力密度,这是从永磁体内部到周围非磁性空气的磁导率不连续跳跃产生的。
静电力
静电力与静磁力类似,通常表现为表面力。在 MEMS 器件中,静电力无论是作为需要的力还是应避免的力,都需要引起人们的重视。
洛伦兹力
根据下面这个我们熟知的公式,只要有电流,就存在洛伦兹力:
其中, 是电流密度,
是磁通量,
是力密度。
磁通量 可以由电流
直接或间接产生,也可以从外部产生。
两根载流导线内部的洛伦兹力密度,其中的恒定电流向相反的方向流动。力密度在导线和周围空气横截面上用黑色箭头进行可视化,磁通量用不同的颜色(大小)和等值线来显示。其中一根导线中的洛伦兹力密度源于自感应磁场和相邻导线的磁场。这里的净力为斥力。
集总电路参数
在电路领域,基本的物理量不是电场或磁场,而是集总电路参数,比如电阻和阻抗。这些电路参数通常描述电压与电流之间的关系,并对电磁装置相关的系统级信息进行编码。
发布日期:2019 年 4 月 3 日上次修改日期:2019 年 4 月 3 日
