
本文是地热能系列博客的第二篇,将重点探讨传热与地下水流耦合的过程,并据此确定地下储藏的热量是否足够多,是否值得开采以获得地热能。文中,我们将通过一个地下水换热回灌系统示例模型演示这一耦合过程。
深层地热能:潜能巨大,风险也巨大
地热能开采的最大挑战之一就是如何将勘查风险降到最低。例如,如何确定所选开采点的热能足够开采 30 年?通常情况下,几乎没有关于当地地下结构及水质等特性的信息,是否值得开采,不确定性相当大。
最近几十年中,数值模型成为评估这一风险的重要工具,通过这种方法可以将不确定性限制在一个合理的范围,然后再进行参数化研究。今天,我将简单地介绍地下水流与传热耦合问题的数学描述,这个问题在许多地热应用中都会遇到。我还将向您展示如何利用 COMSOL 软件研究和预测(水利)地热系统的性能。
地下水换热系统中的方程
可以用下方程描述地下传热:
(1)
热量经传导和对流过程实现平衡,并且可以通过在源项 Q 中定义热量来表示热量的生成或流失。多孔介质传热 接口中有一个特殊的地热采暖 功能,表示为域条件:Q_{geo}。
COMSOL 中还有一个功能可以使地热能仿真工程师的工作稍微更轻松些。目前可以做到的是将热力参数的平均表示实现为一个权重因子,这些热力参数包括岩石基质和地下水,用矩阵体积分数 \theta 表示。对于几种固定的固体和流体,可以选择使用体积平均方法,也可以采用幂律平均方法。
要使用体积平均方法,热传导方程中的体积比热变为:
(2)
热导率变为:
(3)
要正确求解传热,还要考虑与流场相结合。一般而言,地下情况复杂多变,要求我们使用不同的方法对地下水流进行数学描述。如果侧重于微尺度,解决孔隙空间内水的流动,则需要求解蠕动流方程或 Stokes 流方程。对于非饱和区,需要求解 Richard 方程,它常用于有关环境污染的研究中(例如,可以参阅我们之前发表的博客文章:模拟农药径流,涕灭威的影响 )。
而深层地热层中的饱和流及主要由压力驱动的流动则完全可以通过 Darcy 定律求解:
(4)
其中,速度场 \mathbf{u} 取决于渗透率 \kappa,流体的动态粘度 \mu 由压力梯度 p 驱动。然后,将 Darcy 定律并入以下连续性方程:
(5)
如果地质年代较为久远,则由于水流具有储能效应,有关时间的项可以忽略不计。由此,上述方程左边第一项为 0,因为密度 \rho 和孔隙率 \epsilon_p 都可以看作常数。通常,水力属性随温度的变化可以忽略不计。因此,(稳态)流动方程与(时间相关的)传热方程互不相关。在有些情况下,特别是当自由度数量相当大时,利用这种无关性将此问题拆分为一个稳态研究步骤和一个时间相关的研究步骤是很有意义的。
裂隙流和多孔弹性
裂隙流是局部地热系统中主要的水流动态,例如在卡斯特含水层系统中。地下水流模块中包含的裂隙流接口可用于表示二维裂隙和裂缝中的 Darcy 流场。
地下水换热提取系统通常包含一个或多个回灌井和生产井。很多情况下这些井都是单独钻取的,但目前更多的做法是钻取一个(或多个)分支井。还有人提出仅钻取单个井,再分出单独的回灌区和生产区。
需要注意的是,由于水的回灌和抽取而产生的人为压力变化会对多孔介质的结构产生影响,并产生水力压裂。如果考虑这些因素,则还需要进行多孔弹性分析,但在这里我们暂不考虑。
地下水换热应用的 COMSOL 模型:地热回灌
在 COMSOL Multiphysics 中可以非常简单地建立一个对地下水-地热应用作长期预测的模型。
模型区包含三层具有不同热性能和水力属性的地质层,位于一个体积约为 500 立方米的箱体中。该箱体表示处于一个大断裂带上的地热开采点的一部分,层高为源自外部数据集的插值函数。相关含水层已完全饱和,顶部和底部均为弱透水层(隔水层)。温度分布通常是一个不确定性因素,但我们可以假设地温梯度为 0.03 [°C/m],故初始温度分布:T0(z)=10 [°C] – z·0.03 [°C/m]。
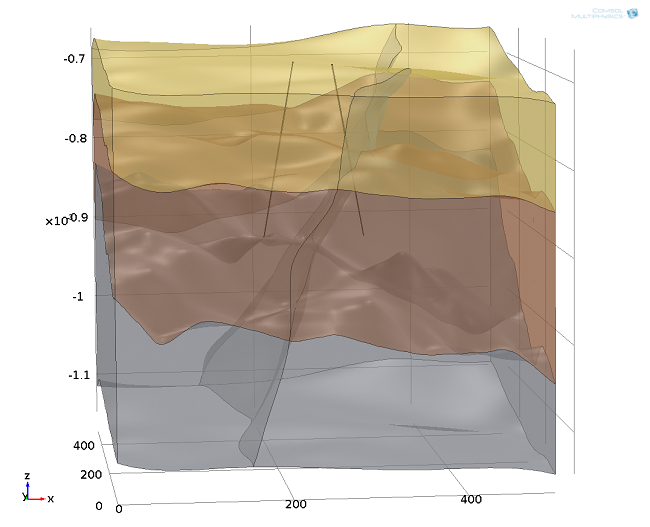
分层地下区域中的地下水换热回灌系统,处于一个断裂带上。边缘长度约为 500m。左侧为回灌井,右侧为生产井。两井之间的横向距离约 120 m。
在 COMSOL Multiphysics 中先对该模型创建网格,然后再对井上的网格进一步细化,从而在此区域获得预期的高温度梯度。
现在,一切准备就绪,可以开始提取热量了!右侧的生产井以 50[l/s] 的速率抽取(开采)地下热水。生产井为圆柱形,之所以采用这一形状是因为它可以满足流体流入流出的边界条件。抽取的热水用于发热或发电后,以同样的速率重新回灌入左侧的回灌井,但水温较低(本案例中为 5[°C])。
经过 30 年热量开采后的流场和温度分布如下图所示:
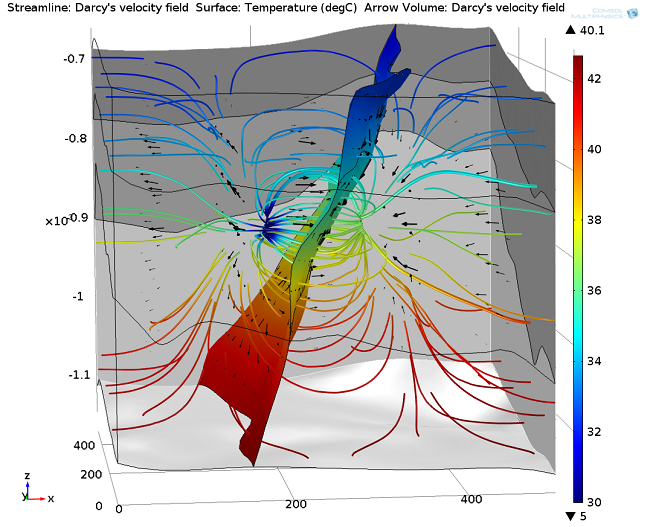
经过 30 年热量开采后的模拟结果:回灌区与生产区的水力联系以及沿流动轨迹的温度分布。请注意,这里只考虑了回灌井区域和生产井区域。其余的钻井未作模拟,以减少网格划分所需的大量计算。
该模型非常适合评估不同条件下某一地热点是否值得开采。例如,回灌井与生产井之间的横向距离是如何影响开采温度的?是否需要扩大横向距离,还是中等距离就已足够?
为此,我们可以改变井距,进行参数化研究:
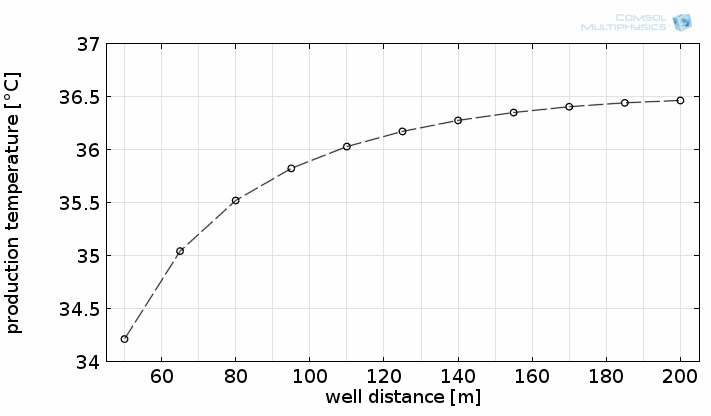
横向距离不同时两井之间的流动轨迹和温度分布。图片显示开采温度稳定后与横向距离的函数关系。
利用该模型,只需改变回灌井/生产井的位置即可轻松获得不同的钻井系统。例如,以下为单井系统的模拟结果:
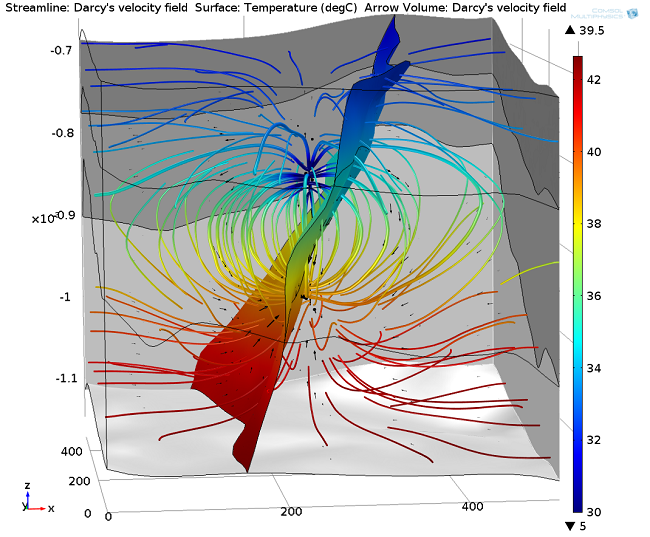
经过 30 年热量开采后的单井方法结果。回灌区(上方)和生产区(下方)之间的垂直距离为 130 m。
至此,我们在讨论含水层时均未涉及周边地下水流的情况。如果考虑地下的水力梯度所引起的地下水流,那会怎么样呢?
下图显示的情况与上图相同,只不过图中的水头梯度为 \nablaH=0.01 [m/m],从而产生了一个叠加流场:
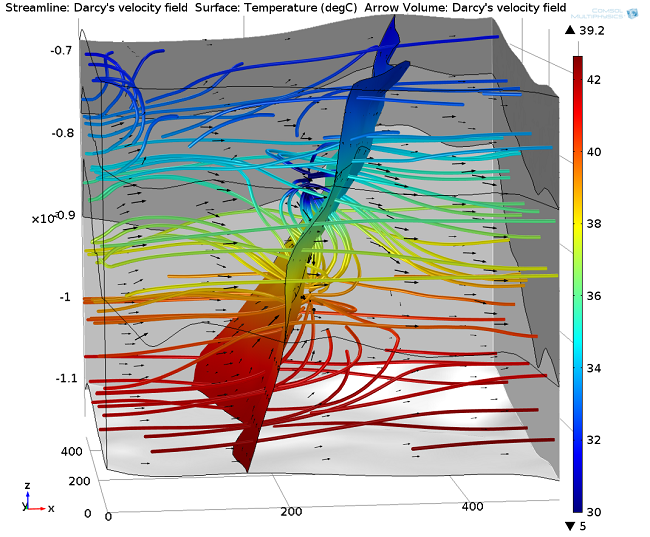
经过 30 年热量开采后的单井及水平气压梯度产生的叠加地下水流。
延伸阅读
- 地热回灌教学模型
- 探索地下水流模块
- 阅读“地热能”系列的第一篇博客:使用 COMSOL 软件模拟地热过程
- COMSOL 用户年会上展示的相关论文和学术海报:
- Full Coupling of Flow, Thermal and Mechanical Effects in COMSOL Multiphysics® for Simulation of Enhanced Geothermal Reservoirs
- Multiphysics Between Deep Geothermal Water Cycle, Surface Heat Exchanger Cycle and Geothermal Power Plant Cycle
- Modelling Reservoir Stimulation in Enhanced Geothermal Systems





评论 (5)
chunhu zhao
2017-12-28该案例是否可以分享?
Phillip
2017-12-28 COMSOL 员工感谢您的关注。 该模型可以在这里找到:
http://cn.comsol.com/model/geothermal-doublet-29751
祝你好运!
春伟 周
2019-06-17您好,这个案例是不是有错误的地方,我算了好几次都是可以显示流线但是整个模型的温度场没有发生变化,裂隙面的温度场始终都是一样的。
鹏超 席
2021-02-23您好,请问,gocad的地质模型导入comsol,并修改原始曲面的过程,可以分享下吗?
宏达 高
2022-04-06如何做出井距和采出温度的动画和曲线