求解线性稳态有限元模型

本篇博客是求解器系列的首篇博客，将介绍用于求解所有线性稳态有限元问题的算法。虽然我们在博客中基于一维有限元问题进行介绍，但所讲解的内容具有普适性，能帮助您理解博客系列中接下来将介绍的更加复杂的非线性多物理场的求解技巧。

什么是线性稳态有限元模型？

考虑下图所示的系统：弹簧的一端固定在刚性壁上，对另一端施加力。

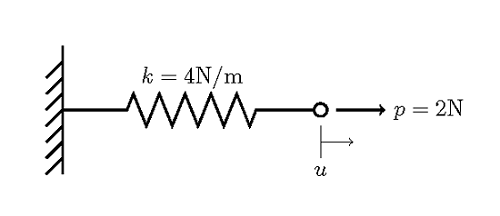
我们希望求出弹簧受力端的位移。使用有限元方法得到一个单个单元的有限元模型。弹簧即为单元，并且两端各受限于一个节点。一个节点固定在壁上，另一个节点由于施加载荷而变形。现需求出施加载荷造成的末端位移。这是一个 线性问题，因为材料属性（弹簧常数）和载荷都与解无关。这同时又是一个 稳态问题，因为我们在求解时假设时间不变。

对模型求解

这个问题只用纸和笔就可以求解，不过我们这里将介绍对此类问题的一个更加严谨的求解方式。对需求解位移的节点进行分析，并画出受力平衡时的图像：

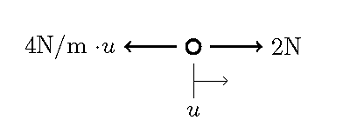
以上受力情况可写成：f(u)=p-ku，即系统方程，受力平衡（稳态条件）时方程值为 0。我们需求出 f(u)=0 时的 u 值。可以将该方程绘制为：

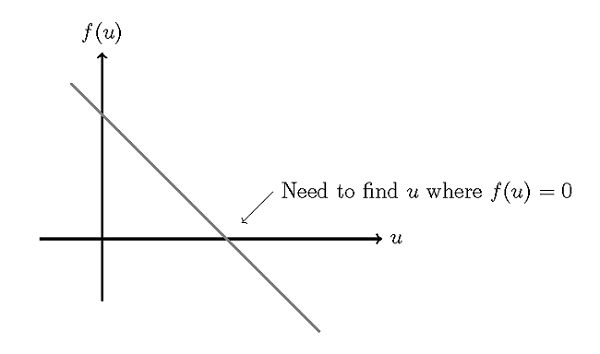
在本案例中我们自然可以通过解析方法求解，但总体来说， u 可能是一个包含几百万未知量的矢量，所以需要更为严谨地处理。以下为精确的算法：

1. 选择一个初始猜测值，例如：u_{init}=0
2. 根据初始猜测值计算方程的值：f(u_{init})=2-4(0)=2
3. 对方程求导：f'(u_{init})=-4
4. 计算解：
   u_{solution}=u_{init}-[f'(u_{init})]^{-1}f(u_{init})=0-(2/(-4))=0.5

以上的算法也被称为 Newton-Raphson 迭代法。此外还可将其绘制为：

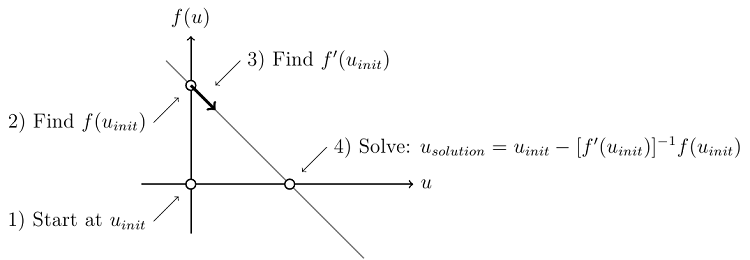
需注意的是，不论从哪开始，都可以在一步之内完成求解。所以每当您使用 COMSOL Multiphysics 求解线性稳态有限元问题时，软件都会根据以上算法求解。以上示例中仅包含一个未知量，所以我们只需求解一个线性方程。通常您的模型中会包含几千甚至几百万未知量，意味着您需要对线性方程组求解，但思路一致。

最后我们来解决数值缩放的问题。当使用电脑求解问题时，由于 浮点数表示法，我们都需要考虑到 有限精确度的问题。电脑无法完美表示实数的空间。为了最小化其影响， COMSOL 会在求解前对等式应用一个比例因子。 COMSOL 会自动为模型中所设定的每一个场变量选择适合的缩放比例，几乎不需要用户操作，但我们还是应该了解一下比例因子的作用。只要其数量级在解中包含值的平均大小的几个数量级之内，就不需要进行交互。除非缩放比例和期望解的数量级差别很大，那就应更改比例因子。

求解线性稳态有限元模型的要点归纳：

1. 不论采用哪个初始猜测值，都可以通过一步迭代求解。
2. 使用变量的缩放比例来解决浮点算法的有限精度问题。

如何读取 COMSOL 日志文件

日志文件

现在我们来了解如何使用上述信息来读取一个典型的线性稳态有限元模型的 COMSOL 日志文件。以下是一个热应力问题的日志文件（已添加行号）：

1) 求解器 1 中的稳态求解器 1 开始于 2013.04.30 17:41:45
2) 线性求解器
3) 求解的自由度数量： 3651 （加上 124 个内部自由度）
4) 找到对称矩阵
5) 相关变量的缩放：
6) 位移场（材料）（mod1.u）：0.0090
7) 温度（mod1.T）：2.9e+002
8) 迭代数      阻尼       步长    #Res #Jac #Sol
9) 1         1.0000000   4.7e-017    1    1   1
10) 求解器 1 中的稳态求解器 1 ：求解时间： 0 秒
11)                                  物理内存： 878 MB
12)                                  虚拟内存： 879 MB
 

注释

• 第 1 行报告了求解器的种类和开始时间；
• 第 2 行报告了软件将指令下达给线性系统求解器。（ COMSOL 可以自动判断线性和非线性问题，并会下指令给相应的求解器。）
• 第 3 行以自由度数量（ DOF ）的形式报告了问题的大小。内部自由度（当其被全部使用时）通常被用于计算边界通量，且不会对问题的大小产生显著影响。
• 第 4 行报告了待求有限元矩阵的种类。
• 第 5-7 行报告了缩放比例。在本案例中求解了一个热应力问题，所以 COMSOL 缩放了位移和温度场。位移场缩放为 0.0090 ，并且使用模型（米）的单位系统，所以只要结构位移不小于 9 纳米（或者大于 9 千米！），那么该位移缩放是可以接受的。温度常的比例因子为 293K 。除非我们在求解一个低温问题（温度大约在 4K+/-0.001K ）或者温度高达几百万开尔文的问题，这个缩放都是可以接受的。
• 第 8-9 行报告了求解中使用了一次 Newton-Raphson 迭代法。
• 第 10-12 行报告了求解时间和内存要求。

现在您应该已经了解 COMSOL 如何求解线性稳态有限元问题，以及怎样读取日志文件。