扬声器阵列的主要设计目的是实现比单个扬声器更广的声音覆盖范围。同时,阵列的辐射方向图必须与单个扬声器的辐射方向图毫无区别。使多个扬声器产生呈放射状分布的声音的一种方法是使用贝塞尔面板。工程技术人员通过分析贝塞尔面板系统的基准模型,可以优化扬声器阵列和其他声学系统的设计。
贝塞尔函数与贝塞尔面板
在 19 世纪,德国数学家和天文学家 Friedrich Bessel 在研究行星运动时使用了 Bernoulli、Euler 及其他科学家之前用过的函数,这些函数后来被称为贝塞尔函数,在声学领域有着广泛的应用。贝塞尔函数可以用来分析圆膜的振动,比如鼓的振型.的沿径向部分。这些函数还可以表明具有独立输入信号的无限阵列扬声器如何实现与单个扬声器相同的声音分布模式。
1983 年,飞利浦公司基于贝塞尔函数的理念,获得了一种扬声器系统的专利,它被称为贝塞尔面板,这种面板可以提供一种方法来布置低成本的标准扬声器来产生呈放射状分布的声音。这种扬声器不仅价格低廉,还可以在不使用有源器件或无源器件的情况下进行组装。

典型贝塞尔面板组合中每个扬声器的装配和输入。
虽然贝塞尔面板如今并不常用,但它们是分析扬声器声音分布的一个很好的着手点。贝塞尔面板基准模型表明,使用 COMSOL Multiphysics® 软件和附加的声学模块对于这种类型的近场和远场声学分析是一种行之有效的方法。
利用 BEM-FEM 混合方法为贝塞尔面板建模
贝塞尔面板的模型几何结构由多个扬声器组成,每两个相邻扬声器之间相距 0.5 米,一个长方体围绕点阵列周围延伸 0.2 米。
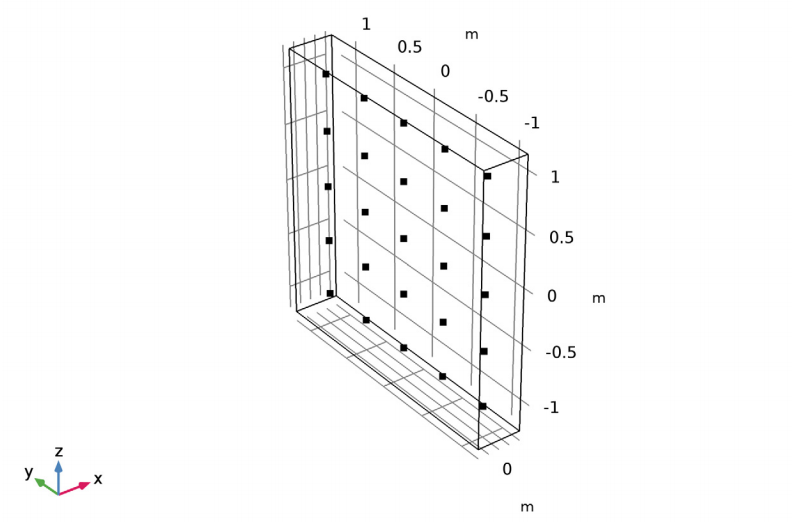
贝塞尔面板模型几何结构示意图。
以相同模式排列的五个贝塞尔面板近似一个纯辐射声场。每个面板由五个扬声器组成,它们排成一行,间距相等。对于这个系统,输入(电压和电流)由因子 1、2、2、-2 和 1 加权,因此我们得到极坐标下均匀的远场分布。
为了求解理想化扬声器面板的声辐射,我们可以采用混合方法来充分利用边界元法(BEM)和有限元法(FEM),混合方法从 COMSOL Multiphysics 软件的 5.3a 版开始提供。有限元法用于模拟点源周围的声学现象,边界元法用于模拟其余辐射问题。我们可以使用以下接口之间的内置 BEM-FEM 多物理场耦合来确定计算域外的声压:
- 压力声学,频域
- 压力声学,边界元
这些接口求解亥姆霍兹方程,并将仿真结果与设为变量的解析解进行比较。
将边界元法和有限元法耦合使用,并对模型的外部域使用边界元法,这种做法具有一定的优势。比如,我们无需使用辐射条件或完美匹配层(PML)来模拟开放域,但如果只使用有限元法,则必须这样做。实际上,在这种情况下,边界元法就像结合了远场计算的理想化辐射条件,从而避免使用远场计算特征。
验证仿真结果
首先,我们来看看近场分布的结果,特别是 200 Hz 时的声压分布和声压级分布。观察靠近扬声器面板的切面中的声压分布,我们可以看到,声源附近的声场不是很均匀,这与方向性有关。如果你正对着一个扬声器,你听到的声音会具有平坦的频率响应,而不是正对着扬声器的人听到的声音则更均衡。
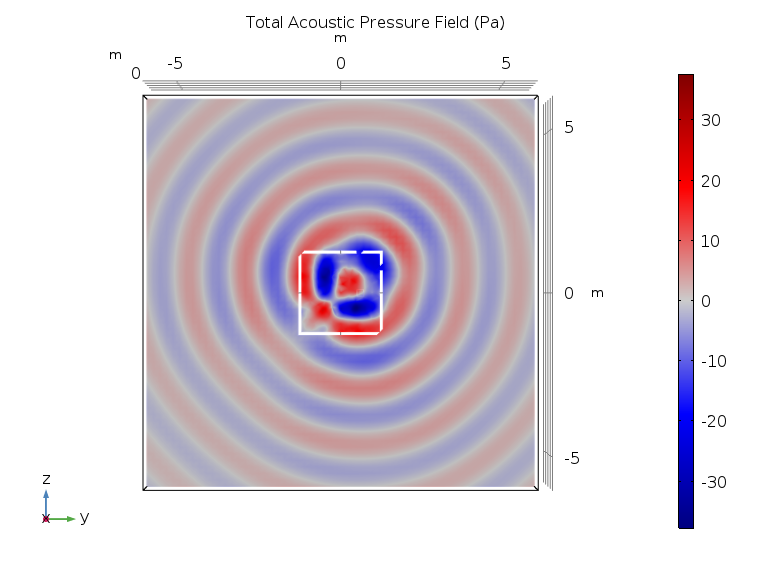
200 Hz 时的声压分布。切面平行于 yz 平面,位于 x = 0.2 米处。
接下来,我们看看同一切面区域周围(x = 0 米)的声压级分布。由于声压叠加(取决于距离以及扬声器之间的间距),因此像贝塞尔面板这样的阵列可以提供更高量级的声压级分布。我们可以改变贝塞尔面板的组合和排列来调整声音的集中情况和分布方向。
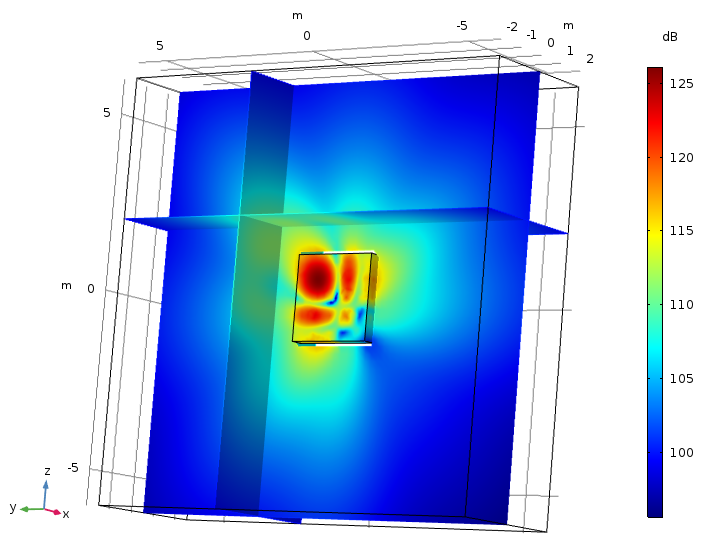
200 Hz 时的声压级分布。切面平行于 yz 平面,位于 x = 0 米处。
接下来,我们看看离扬声器 100 米处的远场分布。由于比例限制等于声压级的全局极值,我们可以在下面看到,任意两个给定方向上的声压级相差不超过 3 dB,这意味着无论受试者的位置如何,声音质量和分布都是相似的。

距离扬声器 100 米处的声压级(dB),用三维远场极坐标图表示。
我们可以通过比较下图中的求解结果(蓝色)与解析解(绿色),来分析距离扬声器 100 米处的不同角度的声分布。绘图显示在此径向距离计算的远场声压与正 xz 平面中极角的关系。计算的求解结果与解析解非常接近,我们还可以通过细化网格来略微提高精度。
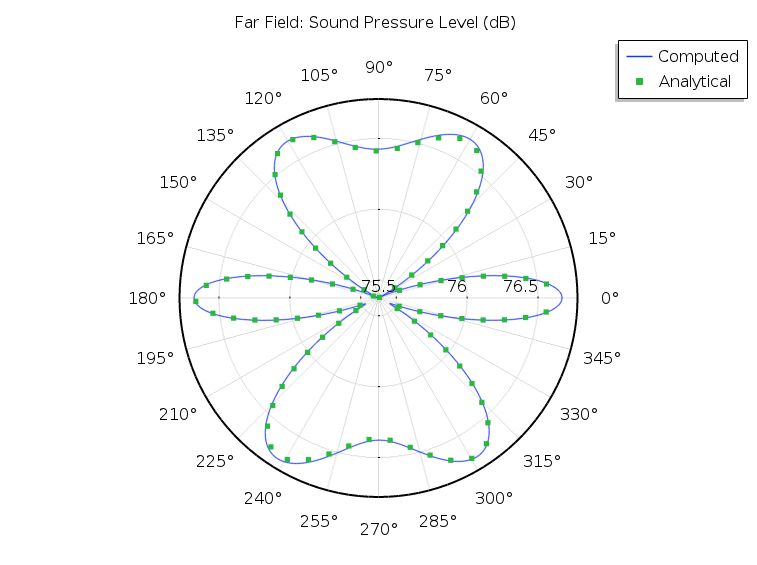
xz 平面中径向距离为 100 米处的声压级(dB)随着从 xy 平面开始的极角的变化情况。
COMSOL® 软件可以生成与声学基准模型相符的可靠结果。通过将边界元法和有限元法结合使用,你可以对声分布声学设计执行稳健的分析。
后续操作
尝试操作贝塞尔面板模型:单击下面的按钮进入“案例下载”页面,你可以从中下载分步教程及附带的 MPH 文件(需要 COMSOL Access 帐户和有效的软件许可证)。
- 浏览以下关于扬声器设计的博客文章:
- 了解有关在声学建模中使用边界元法和有限元法的更多信息:






评论 (0)