通过二维轴对称建模分析扭转问题

你知道 COMSOL Multiphysics^® 软件中的二维轴对称固体力学 接口可以分析扭转和弯曲吗？从6.0 版本开始，你可以在 COMSOL Multiphysics^® 中使用这项扩展功能轻松设置二维轴对称模型，而在这之前分析扭转和弯曲通常需要建立完整的三维模型。使用扩展公式，你可以研究由于轴向力而扭转的各向异性材料、扭转加载的周向裂纹或弯曲的应力集中系数，所有这些研究都是在二维几何结构中进行的。今天的博客文章，让我们来看看如何使用这项功能。

什么是二维轴对称？

在之前的博客文章：平面应力和平面应变的区别是什么？中，我们通过对面外方向上的应力或应变场进行假设，讨论了使用平面二维近似分析三维实体对象的方法。二维轴对称是将三维零件简化为二维几何的另一种方法。二维建模的优势在于，它比构建完整的三维模型计算更精简，同时还允许更简单的应用边界条件和更简单的划分网格。

在二维轴对称中工作需要几何（通常但并不总是）、载荷和约束在对象的圆周上保持不变。如果满足这些要求，就可以仅使用一个二维截面来求解运动方程。通过在整个旋转过程中积分控制方程，二维截面足以恢复完整的三维应力状态和应变状态。二维轴对称分析的典型对象是压力容器、扬声器模块、流体混合器、O 形圈或轴。

典型的二维轴对称分析：一个三维轴（左），在其顶部（中心）施加轴向载荷的二维轴对称几何表示，以及重新获得的三维剖面图显示了 von Mises 应力分布（右）。

默认情况下，只有在二维轴对称中求解的径向 和轴向 位移 u 和 w。圆周分量 v 假定为零。但是，可以包括圆周位移，它允许在二维轴对称中扭转变形。为了更好地理解扩展功能的应用，我们先复习一下通常如何使用位移梯度来描述变形。如果你熟悉这个概念，可以跳过下一节内容直接阅读后面部分。

位移梯度

固体力学 接口求解运动方程或牛顿第二定律。默认的 线弹性材料 节点中的 方程 部分显示了以体积载荷表示的我们所熟知的定律“质量乘以加速度等于所有力的总和”，以及应力和应变之间的线性关系，这是此特殊材料模型明显特征。

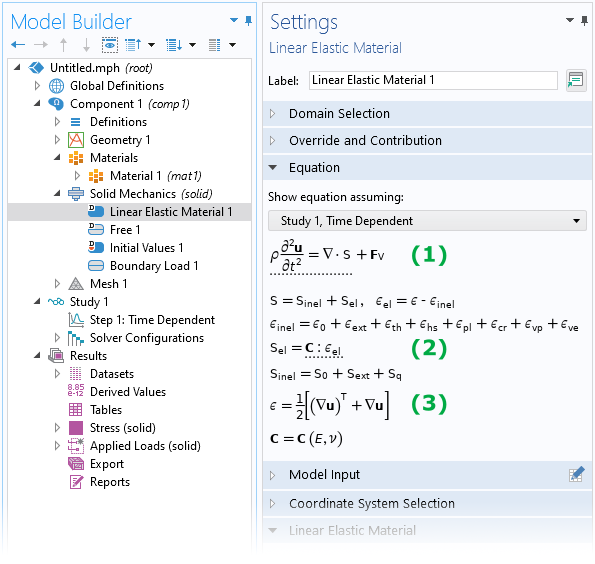
线弹性材料节点 的 方程 部分显示了运动方程 (1) 和线弹性本构方程 (2)，以及工程应变 (3) 的定义。

为了在连续介质力学分析中建立本构关系，有必要使用某种合适的度量来描述材料在任何给定点的变形。实际上，在表征变形时有许多测量方法可供选择，例如 工程应变（参见上图中的 (3)）、格林拉格朗日应变 或 对数应变等。到底哪种方法有用取决于背景，例如使用特定材料模型或模型是否涉及大变形（几何非线性）。然而，所有这些方法都可以表示为位移梯度的函数 \nabla \mathbf{u}，(有时表示 \textrm{grad} \, \mathbf{u})。

那么，什么是位移梯度，它来自哪里？考虑一个（无限小的）小的“块”材料，它可以是任何更大结构的一部分。在初始时间 t_0，该块有一个参考配置（见下面的灰色表面）。在稍后的某个时间 t，该块可能已经经历了刚体运动（平移和旋转）以及变形（拉伸或剪切），如下面的动画所示。

平面二维对象的平移、旋转和弹性变形（纯剪切），视图显示了单独的变形步骤。在 块变形之后，位移梯度用于描述两个初始相邻点之间的位移变化，例如 \textrm{P}_1 和 \textrm{P}_2

在动画中，\textrm{P}_1 和 \textrm{P}_2 两个点已经被标记出来。假设它们彼此无限接近。最初，\textrm{P}_1 点位于 \mathbf{X} 处，而它在当前时间 t 的位置表示为 \mathbf{X}。点 \textrm{P}_1 的新位置也可以用原始位置加上位移矢量来描述，即 \mathbf{x} = \mathbf{X} + \mathbf{u}(\mathbf{X}, t)。

现在，我们把注意力放在邻近点 \textrm{P}_2 上。与第一个点类似，一段时间后 \textrm{P}_2 也会移动到一个新的位置 t。唯一的区别就是点 \textrm{P}_2 距离 \textrm{P}_1 很近，也就是说，它的初始位置是 \mathbf{X} + \textrm{d}\mathbf{X}。因此，当块变形后，\textrm{P}_2 新的位置是

将这个关系稍微重新排列后得到一个表达式 \textrm{d}
\mathbf{x}，是点 \textrm{P}_1 和 \textrm{P}_2 在变形配置中的一小步。

式中，位移梯度 \nabla \mathbf{u} 被定义为张量，当物体变形时，它将 \textrm{d}\mathbf{X} （在初始配置中）映射到点 \textrm{P}_1 和 \textrm{P}_2 之间的位移变化。与这些量密切相关的术语 I + \nabla \mathbf{u} = \textrm{d}\mathbf{x}/\textrm{d}\mathbf{X} 被称为变形梯度（通常表示为 F)，这个量也出现在许多连续介质力学的书籍中。

在更多实际情况中，相对于初始配置（也是材料坐标系的坐标），\nabla \mathbf{u} 是包含位移场 \mathbf{u} = (u, v, w)^\textrm{T} 导数的张量。对于三维笛卡尔坐标系，位移梯度很简单

在二维轴对称中，使用柱坐标系，这时位移梯度被定义为

式中，R, \Phi, 和 Z分别是径向、周向和轴向坐标。

添加扭转…

那么，如何重新定义位移梯度以将简单的二维分析扩展到有时称为 2.5 维的分析呢？

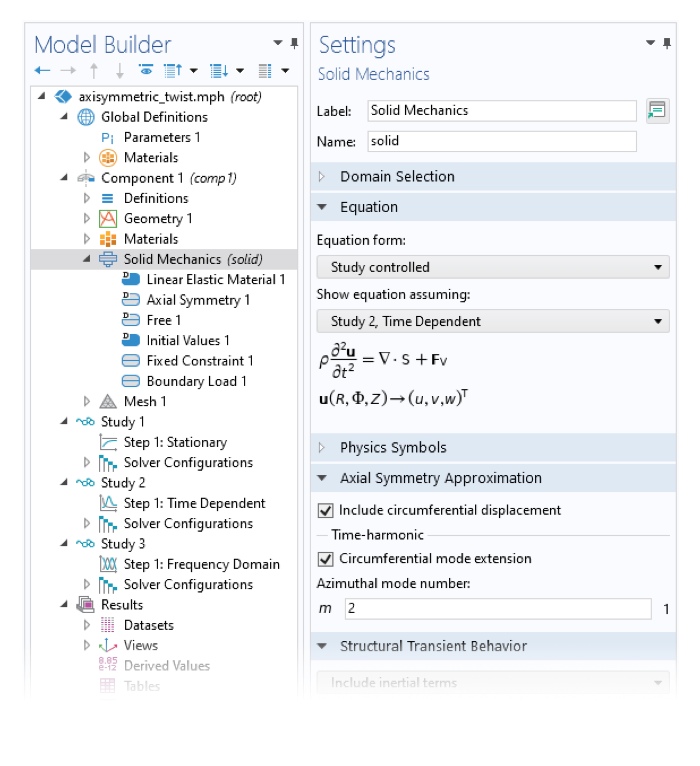
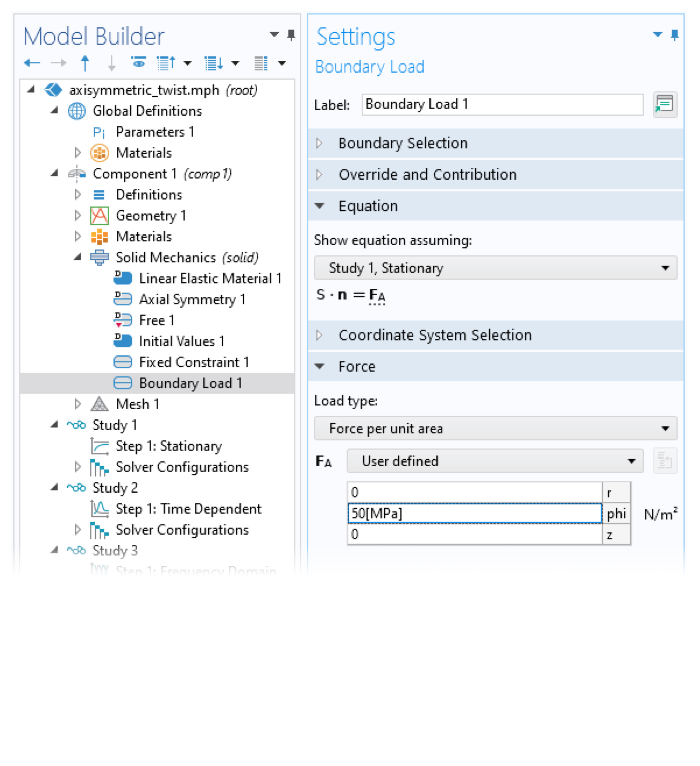
默认情况下，二维轴对称实体的圆周方向位移被假定为零。这是因为有很多应用案例只涉及径向和轴向位移，而将位移分量添加到因变量列表会增加一定的计算成本。因此，为了研究二维轴对称中的扭转，必须明确添加圆周位移。我们可以使用 COMSOL 软件 固体力学 接口 设置 窗口中的 包含周向位移 复选框轻松完成。

轴对称近似 中的复选框启用了二维轴对称模型中的周向位移（左）。选择 包含周向位移 复选框时，模型开发器中的许多节点都显示了附加的用户输入，例如在方位角方向（右）中施加负载的场。

选中 包含周向位移 复选框后，软件会完成三件重要的事情：

1. 添加周向位移分量作为一个新的因变量
2. 显示新的用户输入，例如在圆周方向上施加载荷、弹簧或阻尼
3. 修改位移梯度的定义

最后一步使我们求解面外方向的剪切应变（即\varepsilon_{R\Phi} 和 \varepsilon_{\Phi{Z}})，在典型的二维轴对称分析中，它们被假定为零。唯一的限制是位移场必须围绕物体的圆周保持恒定。换句话说，假定 \Phi 的倒数为零（\partial (…)/\partial \Phi=0）。因此，重新定义的位移梯度为

其中，对于标准的二维轴对称模型，所有涉及 v 的项通常会被忽略。此处描述的扩展功能适用于所有研究类型。

包含周向位移使得通常需要完整三维分析的研究成为可能。下面动画中显示的2个示例就是这种情况。第一个示例显示了由各向异性材料制成的管，例如层不均匀纤维复合材料。在这种情况下，弹性矩阵包含耦合项，这会导致管在轴向拉动时会发生扭转。第二个例子显示了一个带有周向裂缝的容器。它承受的内部压力和周向力，导致裂缝同时受到张开和面外剪切模式的影响。

通常需要完整三维模型分析的示例：由于各向异性材料特性（左）而具有张力–扭转耦合的管的归一化周向位移，以及在开口处加载裂纹的厚壁容器的 von Mises 应力分布和面外剪切模式（右）。

圆周模式扩展

对于特征频率和频域分析，上述限制只允许 \Phi 方向上的一个恒定位移可以轻微提升。对于某些问题，例如扭转振动，假设解在圆周上具有一定的周期性是合理的。这个想法可以方便地用一个复值假设来表示：

这是一个假设线性响应的有效解决方案，这是频域分析最常见的基本假设。是定义位移场中周期数的方位角模式数。有了这个假设，位移梯度变为

这种类型的二维轴对称扩展也称为 圆周模式扩展，可以使用 轴对称近似中的第二个复选框激活（参见上面的屏幕截图）。模式编号必须指定为用户输入。

有两个需要注意的特殊情况：

1. m=0，对应于一个常数移位
2. m=1，可以描述二维轴对称中的弯曲变形

请注意，COMSOL Multiphysics 会自动在对称线上修改轴对称条件 (u=v=0)，以便允许弯曲变形。

下图显示了特征模式的示例，可以使用圆周模式扩展进行研究。通过改变模式数，可以在相应的全三维分析中找到的所有特征模式——前提是基本轴对称假设成立。

m=0
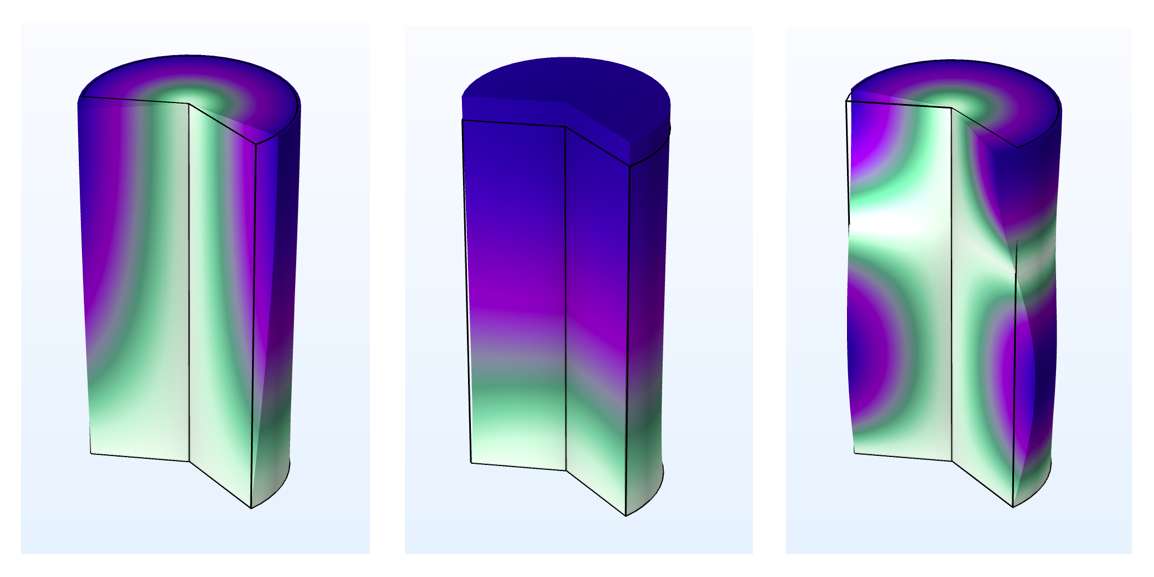
m=1
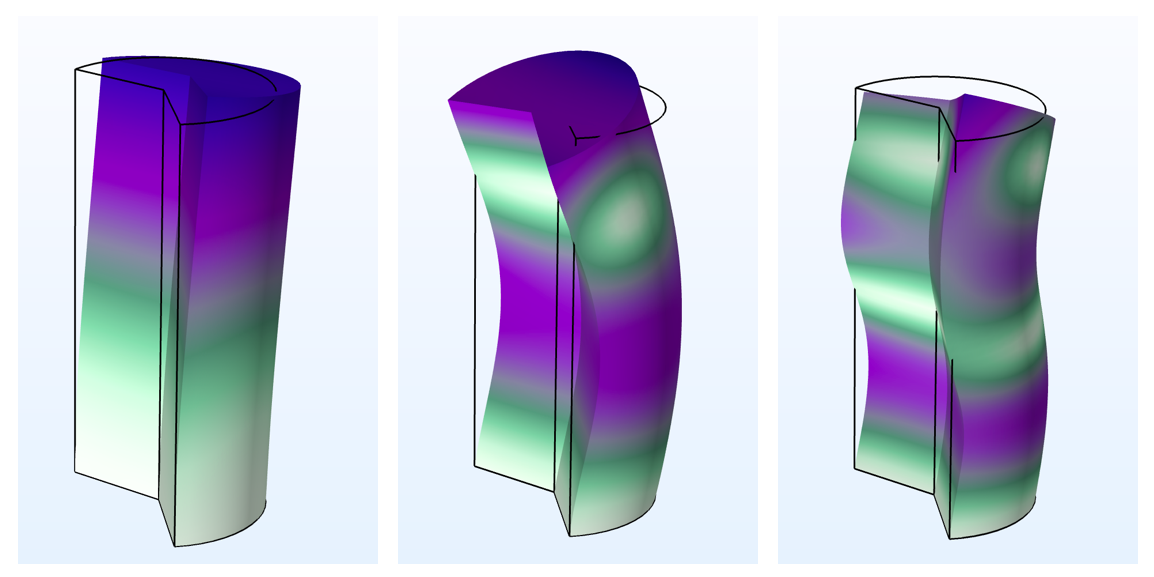
m=2

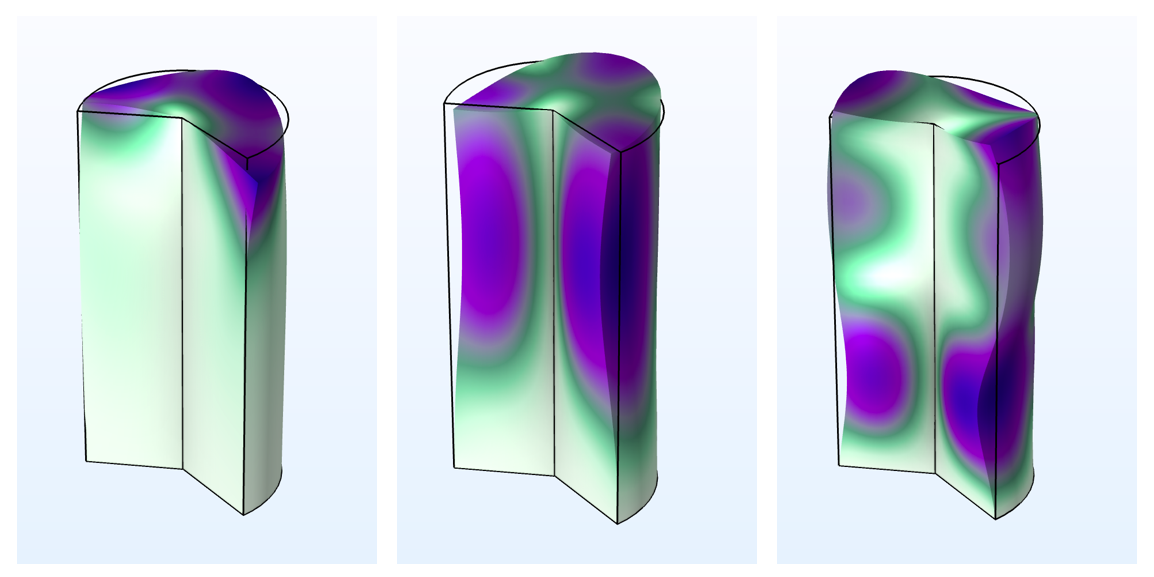
圆柱的前三个特征模态，一端固定用于不同的模态数 m。在这个例子中，m=0 产生扭转和轴向模式，m=1 仅显示弯曲模式，m=2 显示高阶扭转模态。

一般来说，圆周模式扩展只能用于特征频率和频域研究。在稳态和瞬态研究中，圆周位移 v 保持不变，对应于模式编号 m=0。但是，如果在频率为 0\,\textrm
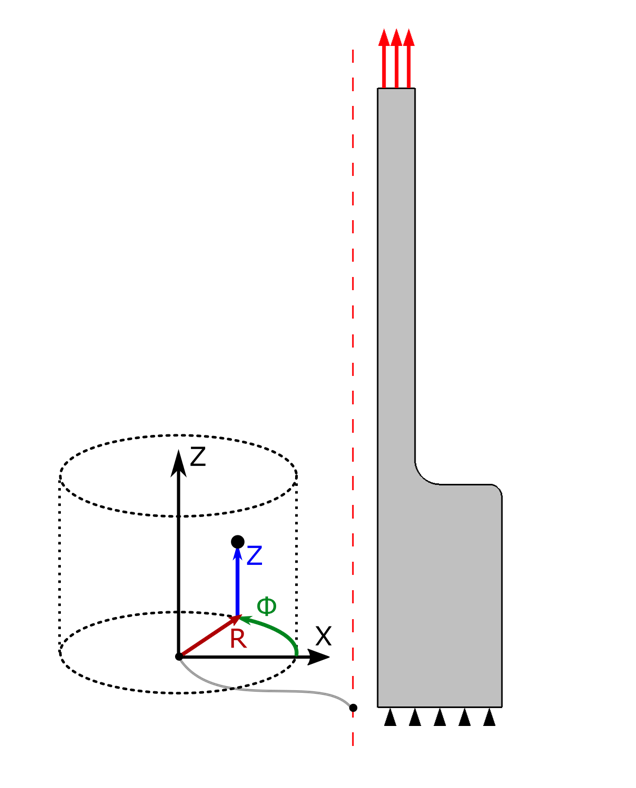
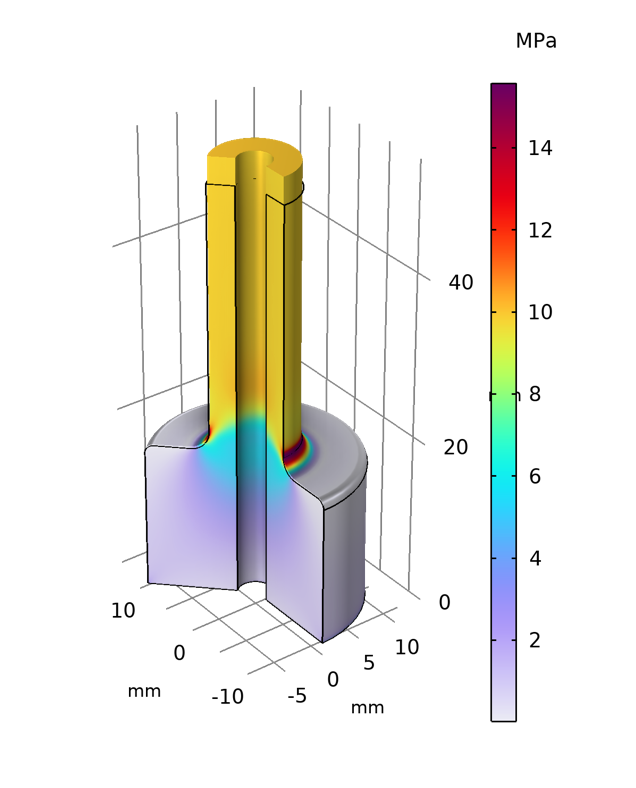
{Hz} 下运行一个频域分析，将得到一个稳定的解，因为所有惯性项都变为零并且所有负载都变得与频率无关。使用这个技巧，可以计算二维轴对称中的静态弯曲变形。下图显示了轴承受弯曲力的示例（模式编号 m=1) 和轴向应力 \sigma_z，与在较薄和较厚轴部分之间的过渡区域中的分析预期应力进行比较。

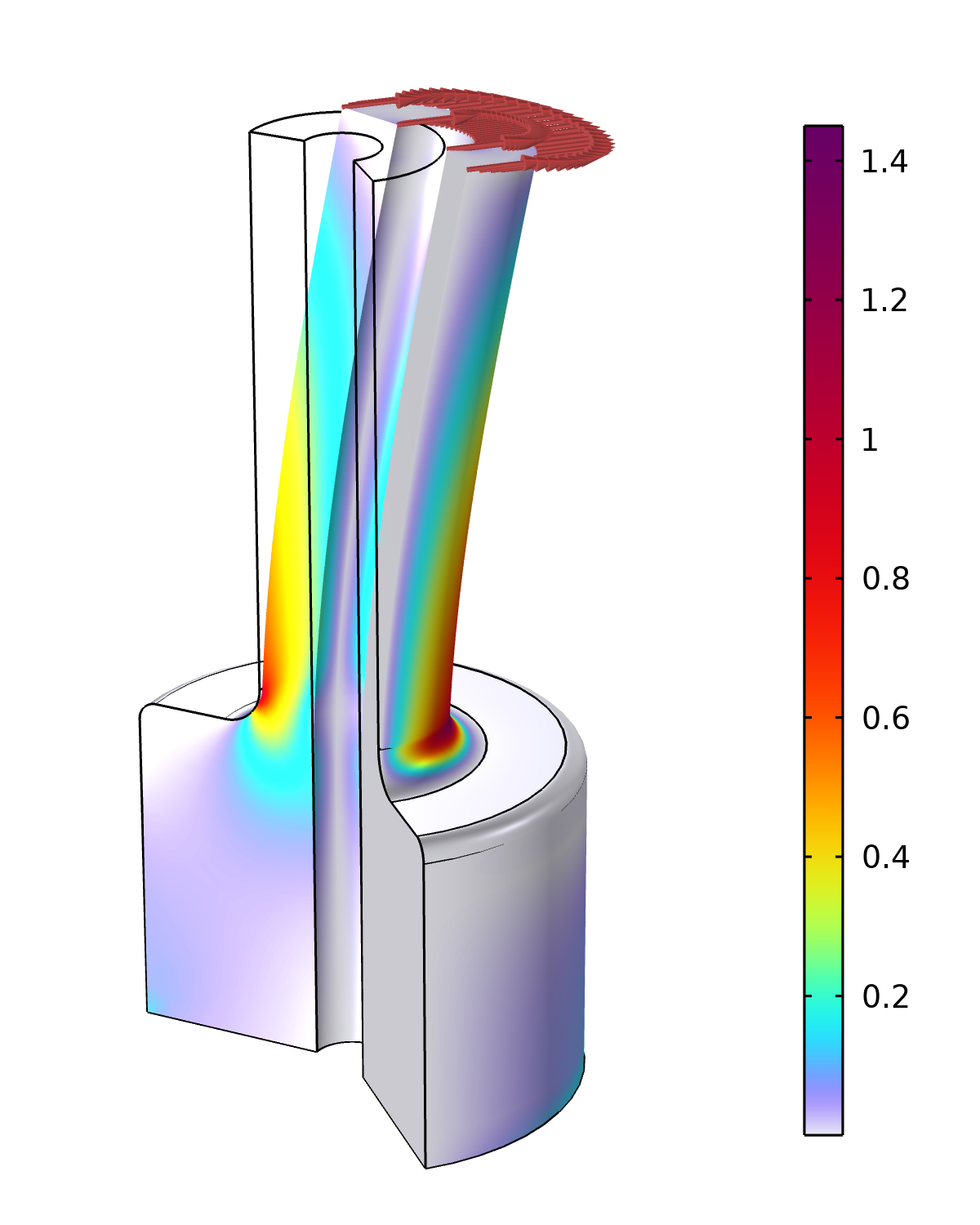
在二维轴对称中模拟的承受弯曲力的轴。该图显示了应力集中系数，或者更准确地说，显示了实际应力之间的比率 \sigma_z，以及从基本弯曲理论中获得的圆角区域中的预期法向应力。

该案例模型，包括在这种情况下如何应用载荷的详细信息可以在文后链接中下载。

其他结构力学接口呢？

为了求解更复杂的位移场，通常用面外自由度扩展具有的二维公式的想法并不是唯一的。例如，壳 接口也支持圆周模式扩展。固体力学 接口中的平面二维等效项被称为面外模式扩展，可以在二维固体力学 设置 窗口中启用。它允许用户模拟面外方向的波状位移。

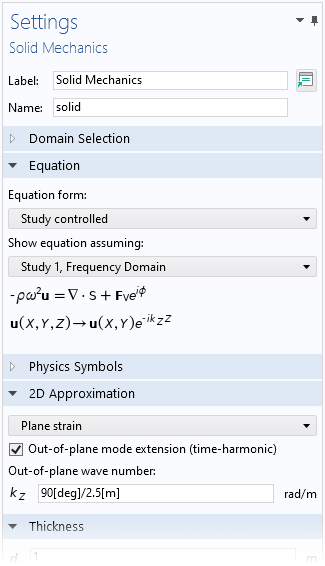
含二维平面应变公式的 固体力学 接口中的 面向模态扩展 复选框。

此外，其他一些物理场接口支持使用类似类型的扩展求解更高级的三维场。例如，在流体接口中，该选项称为 涡流。

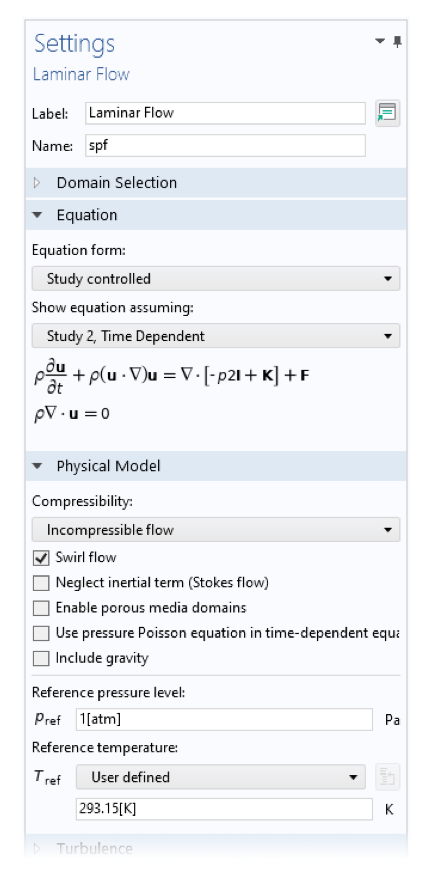
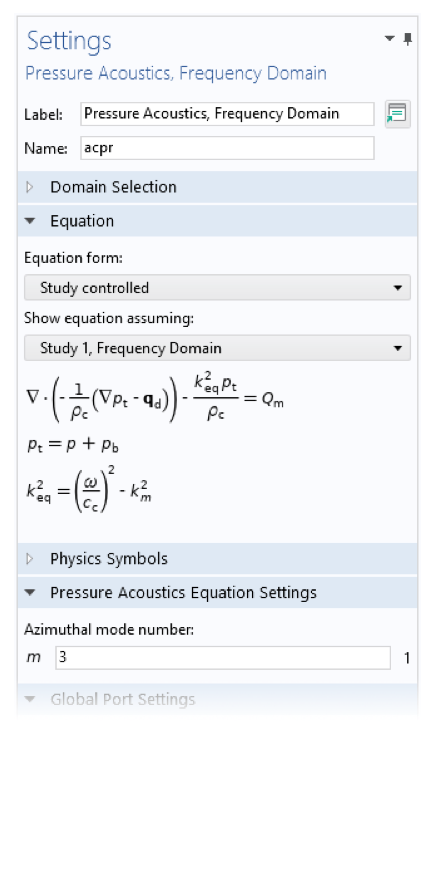
二维轴对称 层流 和 压力声学，频域 接口的设置。漩涡流和 方位角模数设置允许求解圆周方向上形状更复杂的场。

自己动手尝试

想自己动手尝试模拟文中讨论的二维轴对称扭转和弯曲吗？单击下面的按钮访问 MPH 文件。