
在这篇博客文章中,我们将介绍形状优化的概念,即利用分析敏感性的方法来调整零件尺寸。如果您计划改进单个目标函数,或者修改一组几何参数和约束,可以使用 COMSOL Multiphysics 中的“优化模块”和变形几何 接口来发现最优结构,而无需重新剖分网格。我们来了解一下吧!
平行板电容器的仿真优化
我们先来回顾一篇关于计算设计敏感性的博客文章,它演示了如何使用变形几何 接口和“敏感性”研究来分析计算平行板电容器的设计敏感性。针对这一问题,我们计算了电容如何随几何特性和材料属性的变化而变化。此外,我们在未改变几何或重新剖分网格的情况下,计算了几何变化的设计敏感性。接下来,我们计划使用同一个框架来修改电容器的几何结构,目的是借助“优化模块”的功能来最小化某个物理量。
首先,我们对之前的示例进行简单扩展:平行板电容器的边长为 L=1\ m,两块电介质的相对介电常数分别为 \epsilon_{r1}=2, \epsilon_{r2}=4,二者的初始厚度均为 T_0=0.1\ m。此外,我们将忽略所有弥散场,因此只需要模拟两个平行板之间的区域,由此得到下图中的计算模型。
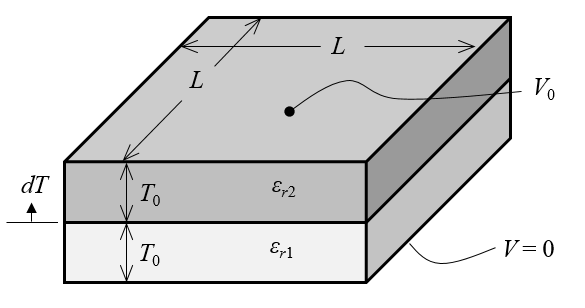
平行板电容器的示意图,其中金属板之间存在两块电介质。模型忽略了弥散场。
我们按照上文描述的尺寸绘制了两个几何长方体,由此构建出模型。静电 物理场接口允许我们向顶面和底面施加电压和接地 条件,并应用材料的介电属性。接着可参考之前发布的博客,对电能密度进行积分,借此计算出电容值:C_{computed}=118\ pF。
现在,假设我们计划通过修改两层电介质的厚度,设计出一个 100 pF 的电容器,同时不改变器件的整体尺寸。这可以算是一个优化问题:
也就是说,我们希望在一定限度内改变电介质厚度,使电介质厚度不为零,且电容尽可能接近 100 pF。在上方函数中,设计参数 dT 表示两层厚度的变化。目标函数本身的形式保证了绝对值大小是统一的。从数值角度看,这一形式优于 (C_{computed}-100\ pF)^2 或绝对值函数 |C_{computed}-100\ pF|。
第一步,我们可以使用变形几何 接口来定义介电层厚度的变化。因为我们希望在计算分析敏感性时不必对改变了尺寸的几何重新剖分网格,所以变形几何 接口是不可缺少的条件。由于我们将修改两个电介质的尺寸,所以希望尽可能完整地定义这些变形。如下方截图所示,我们将借助指定变形 域特征来完成这一任务。
电容器模型最初以原点为中心,因此原始的、未变形的部分拥有自己的坐标系:(Xg,Yg,Zg)。因为介电层的厚度将发生变化,所以对于这个简单的笛卡尔几何,我们可以使用上述坐标系直接定义变形。底层和顶层的变形分别为 dT*(1+Zg/T0) 和 dT*(1-Zg/T0),其中 dT 和 T0 是全局参数。
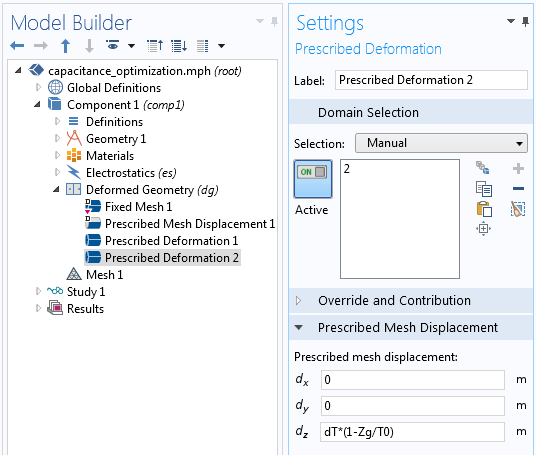
使用 指定变形特征来控制介电层的厚度变化。
接下来,我们看一看优化用户界面。为了解决这个简单的问题,我们可以在研究序列中添加一个优化 特征,如下方截图所示。
如图所示,最小化问题语句和缩放操作完全可以在优化 研究节点中实现。相关设置是目标函数,其表达式为 (C_computed/100[pF]-1)^2,控制参数 是 dT,其初始值为 0[m] 。我们规定了上限和下限,防止出现零或负厚度。最后,我们根据原始厚度 D 对设计参数 dT 进行缩放,使优化值的数量级接近统一。
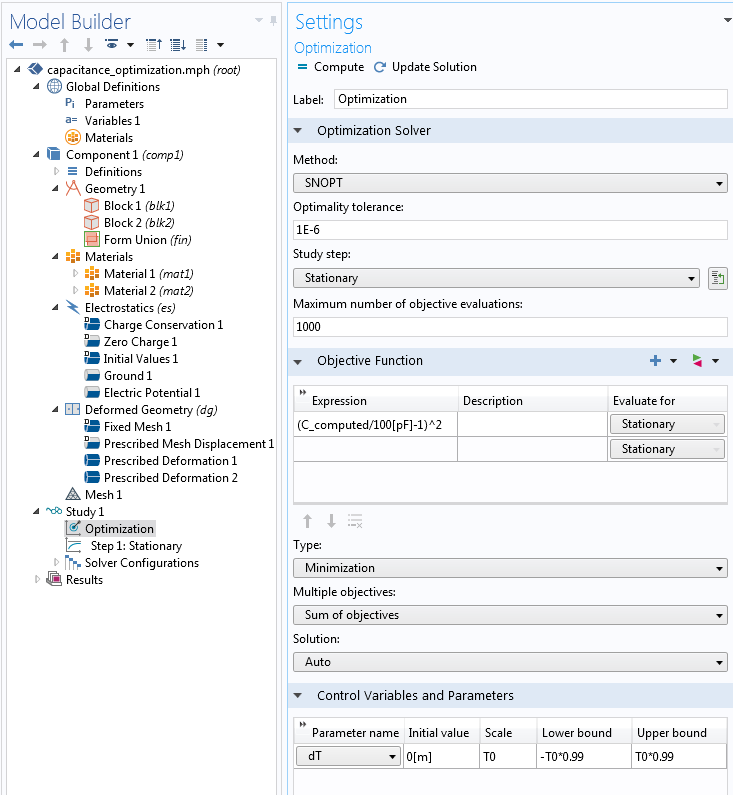
优化求解器的设置。
使用 SNOPT 方法来解决这个优化问题。SNOPT 和 MMA 方法都使用由分析计算得出的敏感性,但是 SNOPT 能最快收敛到 1E-6 的默认容差范围内。最终,器件电容为 100pF,电介质的厚度为 D1 = 0.1542 m,D2 = 0.0458 m。原始模型和优化结构的电压场和有限元网格如下图所示。我们可以观察到,有限元网格被拉伸和压缩,但是没有发生重新剖分。
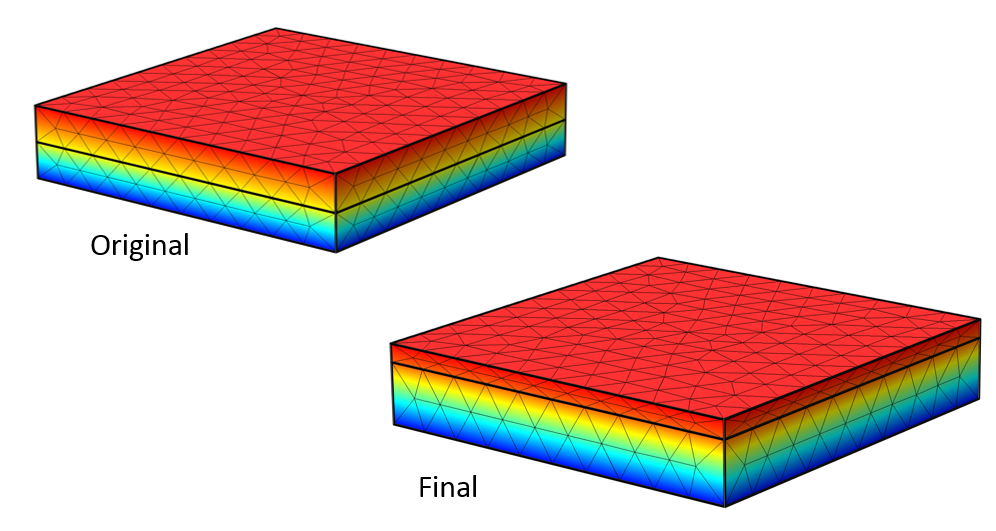
初始和最终结构。图片显示了电压场和网格。
关于形状优化和变形几何的结语
在上文中,我们展示了一个非常简单的形状优化示例,虽然只要稍加努力,我们也能手动或通过执行参数化扫描计算出问题的解。上文演示的几何变形同样十分简单。但是,在考虑更复杂的几何结构和更复杂的几何变化时,您不可能总是使用未变形的空间坐标来直接定义变形。在这类情况下,为了定义变形,您需要向模型中添加方程。当然,除了简单的尺寸变化之外,您也可以考虑更复杂的变形。我们将在下一篇关于优化的博客文章中详细阐释这一主题。






评论 (0)