流体流动计算仿真中存在的一个问题是实验相关问题。尽管我们在 COMSOL 中可以很容易地生成漂亮的三维可视化数值结果,但将这些结果与实验结果进行比较通常比较困难。纹影成像是一种实验技术,它可以生成一组含三维流场的二维图片。事实上,在 COMSOL Multiphysics® 软件中也可以很容易地创建这种成像图。下面,我们来了解更多详细内容。
纹影成像的背景
纹影成像技术的历史可以追溯到很远,甚至可能早于书籍记载。古代穿越沙漠和海洋的旅行者们都非常熟悉海市蜃楼的原理,例如海市蜃楼和 颠倒的帆船等物体的遥远幻影(这可能是导致Flying Dutchman这类寓言产生的原因)。发生这些现象是因为光线在穿过不同密度的空气时会轻微弯曲。这种原理可能在1000 年前就以某种形式被人们所理解,但直到最近 500 年左右,人类才开发出这种实验技术。
虽然纹影成像方法有很多变化,但基本操作原理非常简单。流体(或固体)内的任何温度或压力变化都会导致密度局部变化,而密度会影响折射率。对于大气,折射率 n 与密度 \rho 满足 Gladstone-Dale 关系:
对于可见光,G 约为 0.23 cm3/g。
需要注意的是,上面的表达式只是一个简单的起点,我们可以使用更完整的表达式,对于气体混合物和反应流,还有更复杂的表达式。开发纹影成像实验方法的目的是捕捉到流体中这些密度变化的气流中光学图像。
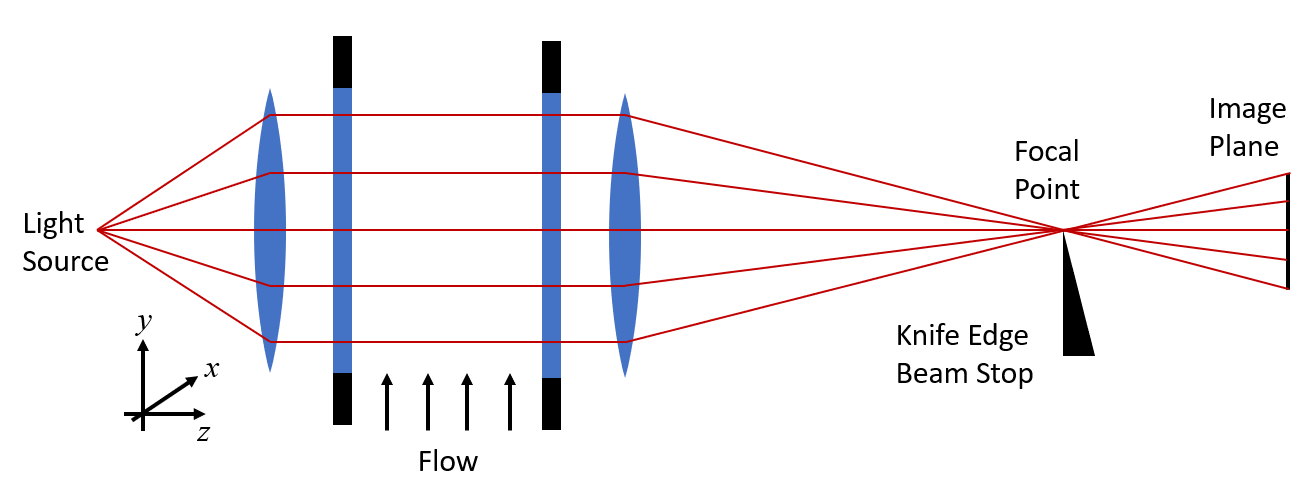
纹影成像设置。
典型的纹影成像实验装置如上图所示。此装置有两个透明的窗口,例如围绕风洞的两侧有一个流场。我们首先假设流场没有变化。在一侧有一个光源,以及一些提供均匀照明的光学元件(透镜或镜子)。通过几何光学方法,我们将这种光视为一组穿过流场的平行光,然后让它们通过另一组将光线聚焦到图像平面上的光学元件。
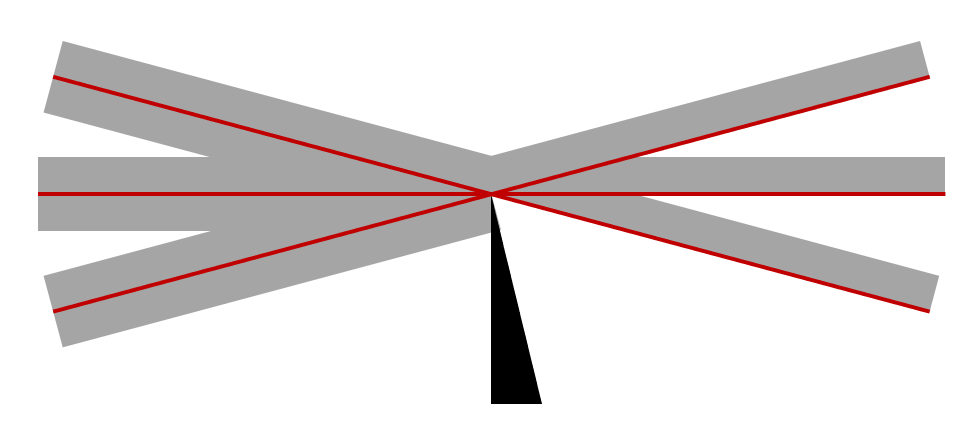
焦点处未受干扰的光线。用刀刃挡住一半的光,并忽略边缘处的衍射。
但是我们要知道,所谓的焦点不是一个单一的点。光不能被聚焦到一个点上;聚焦光束总会有一些有限的半径。你可以通过了解电磁波相关知识来理解这个内容。
但是,对于本文而言,我们只需要了解一个关键点,就是放置在焦点处的障碍物会遮挡一部分光。这已经足够保持这个几何光学方法了。如果我们在焦点处放置一个刀刃(实验上通常是剃须刀片),就可以阻挡全部光线的一半,但仍然可以获得完整的图像,尽管光强只有一半。为了便于理解,我们可以考虑将每条光线看作具有一定的有限厚度,如上图所示。
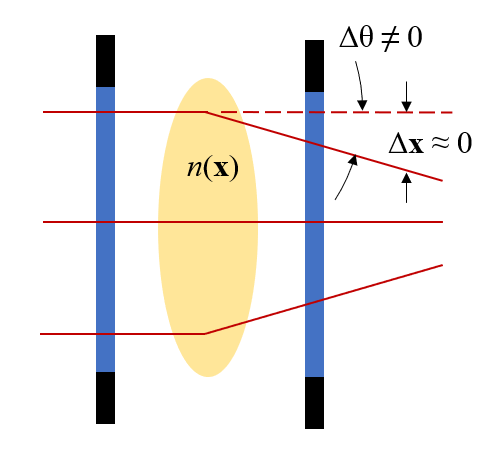
折射率略有变化的区域会稍微改变光线的方向,但不会改变它们在出射平面上的位置。
现在,我们来考虑当流动中存在密度变化时会发生什么。我们已经知道折射率是密度的函数,所以在示意图中引入一个小的折射率变化,看看会发生什么。上图显示了光线的关键行为。跳过整个推导,我们仅强调以下几点:
- xy 平面中折射率的变化将导致光束在沿 z 方向传播时非常轻微地改变方向(角度)
- 假设当光线通过实验域时,光线在 xy 平面中的位置变化可以忽略不计
也就是说,在位置 (x,y) 进入域的任何光线都将离开其在xy平面中的原本位置,但会朝着稍微不同的方向前进。接下来,我们看这对焦点有什么影响。正如我们在下图中看到的那样,折射率的变化会稍微扰乱光线,因此稍微多一点(或稍微少一点)的光线会被刀刃遮挡。这在图像平面上显示为亮区和暗区,并形成基本操作原理。
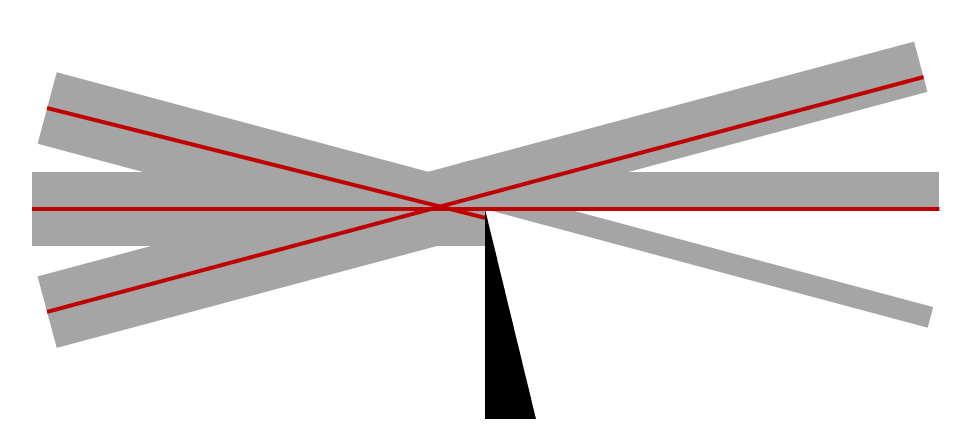
焦点处的扰动光线。对于以略微不同的角度入射的光线,刀刃阻挡的光量不同。
刀刃可以旋转到平行于 x 轴或 y 轴,或者可以被针孔光束挡板代替,每个挡板都会产生不同的明暗图案。纹影图像中的这些亮带和暗带对应于流动域中的以下积分:
| 障碍物类型 | 方程 |
|---|---|
| 平行于 x 轴的刀刃 | \int \frac{\partial n}{\partial y} \partial z |
| 平行于 y 轴的刀刃 | \int \frac{\partial n} {\partial x} \partial z |
| 针孔遮挡板 | \int \sqrt{\frac{\partial n}{\partial x}^2 +\frac{\partial n} {\partial y}^2} \partial z |
事实证明,这些积分在 COMSOL Multiphysics 中实现起来非常简单。
在 COMSOL® 软件中创建纹影图像
在创建图像之前,我们需要先介绍计算流体动力学的一个相关知识:如何处理可压缩流体 。简单来说,出于数值建模的原因,我们经常假设流体具有恒定的密度。从流动模型的角度来看,这是完全合理的。小于约 1% 的密度变化可能不会对速度场或压力场的解产生太大影响,但会显著改变折射率。因此,如果在假设密度不变的情况下对流动进行建模,例如使用布辛涅斯克近似时,请确保使用压力场(如果计算了温度场)对空间密度的变化进行后评估。对于大气空气,宜采用理想气体定律,但请确保这里使用的是绝对压力而不是表压。
一旦我们在建模空间中建立了密度变化的表达式,就可以用它来计算折射率分布以及折射率在一个或两个方向上的导数。为此,我们使用了内置的微分算子。例如,如果密度表达式是变量 rho,我们可以将 x 导数作为 d(rho,x)。我们现在只需要沿流动的方向对该表达式进行积分,并将它们绘制到平行于流动的平面上。为此,我们使用了广义投影算子,我们甚至可以投影到流动域之外的边界上,如果我们希望使用比存在于流动域边界上的网格更精细的网格来评估该算子,这将是非常有利的。
我们还需要考虑当流动中有不透明障碍物时会发生什么。在这种情况下,我们不想用上面的任何一个积分进行求解。我们可以使用从 COMSOL Multiphysics 6.0 版开始提供的CAD 导入模块、设计模块,或 LiveLink™ 产品中提供的工作平面 投影 功能,将任何障碍物的轮廓投影到光学出射平面边界上,并且只评估非阴影表面上的积分。
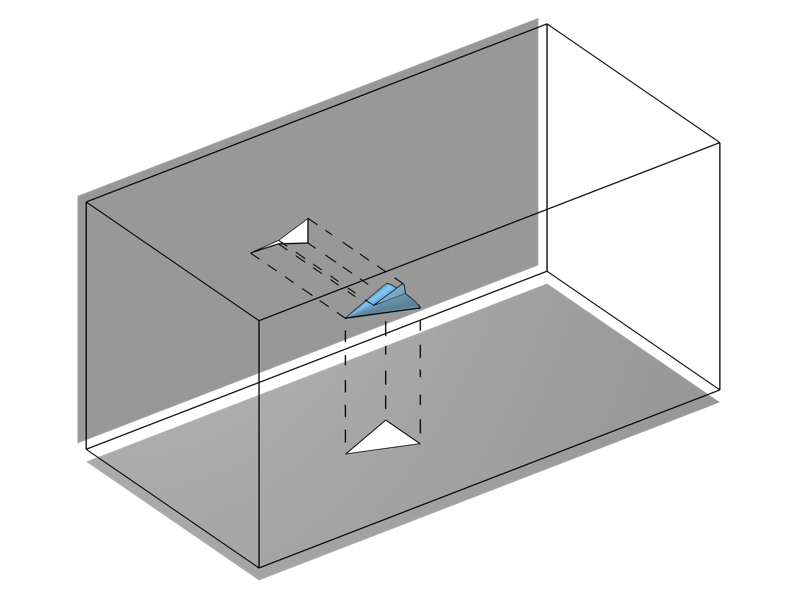
使用 工作平面投影 功能,将几何图形的轮廓投影到平面上。
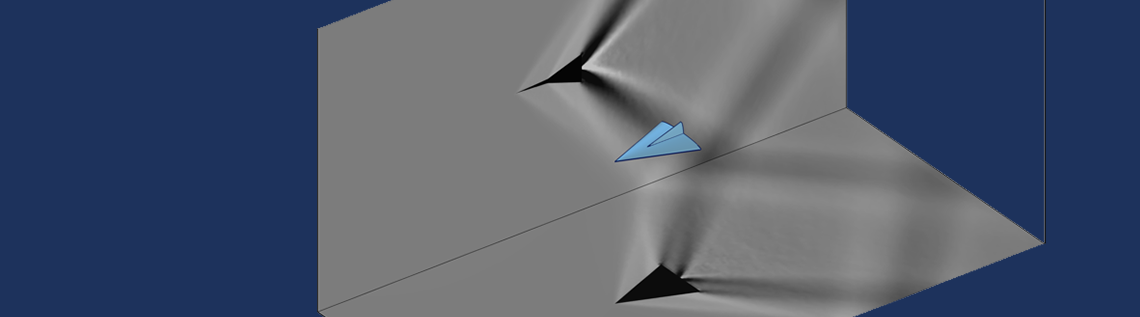
在我们的建模中使用这些技术,可以制作与纹影成像设置的实验结果相关的图。下图是围绕一个物体的高马赫数流模拟,这与 含凸起流道中的超音速三维教程模型中演示的类似。同样的技术也可以用于声学模型的结果可视化研究中。
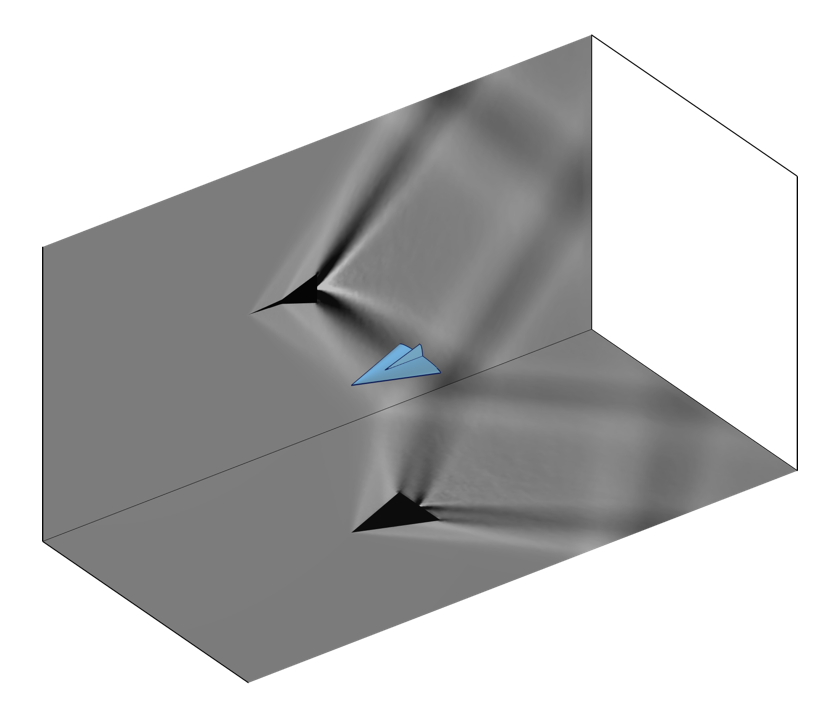
通过 广义投影 算子创建的与超音速风洞流道模型的纹影成像相关的图像。
下一步
想了解有关 COMSOL 软件中 CFD 建模功能的更多信息吗?请联系我们!






评论 (0)