“如果你想知道宇宙的秘密，就用能量、频率与振动来思考。”— 尼古拉·特斯拉
我们能“看见”声音吗？就算不能直接看到，但我们离这个目标已经不远了。通过改变看问题的角度，我们可以了解声学现象的本质。观察声学现象的一种方法是研究称为克拉尼板 的固体介质中的驻波。这是一种特殊技术，可以在板上产生图形，从而揭示声音的物理性质。
将乐器的共振可视化
想象一下你正在一场古典音乐会上，管弦乐队已经完成暖场演奏，灯光也暗了下来。小提琴独奏者来到舞台中央，聚光灯打在她的身上。当她拿起琴弓，全场观众安静下来，你期待着第一个优美的音符响起。演奏者将琴弓拉过琴弦，发出美妙的音符，在整个大厅回荡，带给你愉悦的听觉享受。
表演正式开始之前，乐手们在舞台上暖场。图片由 Jiaqian AirplaneFan 提供，在 CC-BY 3.0 许可下使用，通过 Wikimedia Commons 分享。
除了小提琴演奏者的天赋和日常训练，小提琴的品质对发出的声音也起着很大的作用。音乐家们对自己的乐器非常挑剔，这是理所当然的，因为乐器的设计会影响它的共振。举例来说，当拉动琴弦时，琴弦会以一定的频率振动，该频率通过每秒来回振动的次数进行测量。至关重要的一点是，小提琴的琴桥和琴身需要经过优化才能传递振动的能量，否则只能产生最小的共振。
在设计和制造小提琴和其他弦乐器时，需要测试各个孔的最佳位置、木材的厚度以及内部钢筋的位置等因素。我们还可以通过克拉尼板将小提琴中各种振动的几何形态进行可视化，称为克拉尼图形。
小提琴形状的铝质克拉尼板照片，显示了克拉尼图形。图片由 Stephen Morris 提供，在 CC BY 2.0 许可下使用，通过 Flickr 分享。
克拉尼板是如何工作的？它们又是如何产生的？
恩斯特·克拉德尼：探索流星和音乐
现在我们都知道声音在固体、气体或液体介质中以波的形式传播，但过去人们并不知道这一点。18 世纪末，德国科学家恩斯特·克拉德尼发明了一种方法，将声波的振动可视化，首次证明了声音是通过波来传播的。
恩斯特·克拉德尼在获得法学学位后不久，突然改变了职业生涯，最终成为了著名的“流星之父”和“声学之父”。克拉德尼的父亲是一名法学教授，不赞成儿子对科学感兴趣，迫使他像自己一样，成为一名律师。克拉德尼遵从了父亲的意愿，但在 1782 年从法学院毕业后不久，他就收到了父亲去世的消息。虽然这对克拉德尼来说的确是一段艰难的时光，但从此以后他可以自由地追求自己真正想要的职业，并将研究方向转向物理学。
然而意想不到的是，克拉德尼的法律背景却为他对这门科学的研究带来了优势：他在审查法庭案件的目击者证词方面积累了经验，并使用类似的方法来支持他的理论，即流星来自地球之外，并非源自火山，而后者是当时人们的共识。
克拉德尼极尽所能对从天而降的物体进行了各种研究，并找到目击这些事件以及听到和看到过类似现象（比如大量的岩石落到地面、火球、爆炸和音爆）的人们。在汇编了最可靠的目击者报告后，克拉德尼能够估算出岩石进入大气层的速度，从而得出结论：岩石烧焦的外观和它们极高的速度，只有它们来自外太空才可能解释这一点。
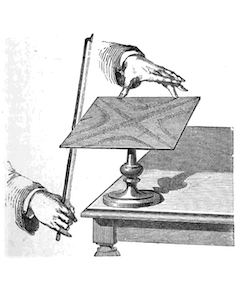
左：恩斯特·克拉德尼。图片来自美国公共领域，通过 Wikimedia Commons 分享。右：克拉尼板技术图解，图片来自美国公共领域，通过 Wikimedia Commons 分享。
不仅如此，克拉德尼还为实验声学铺平了道路。也许正是这位物理学家对音乐的兴趣和能力激发了他对这个领域的追求，他在本杰明·富兰克林和罗伯特·胡克的发明基础上发明了新的乐器，包括 euphone 和 clavicylinder。他带着他的乐器在欧洲各地巡回演出，并向人们演示和解释这些乐器设计背后的科学原理。
他的成就之一是利用风琴管测定气体中的声速，并且还发现了克拉尼定律。这个公式关系到圆平板振动模式的频率。在其他应用中，克拉尼定律可以帮助预测平面上的振动模式，并描述钹和铃铛的振动。
克拉德尼对音乐和声学的兴趣促使他思考乐器的形状和对称性，孕育了让他举世闻名的理念……
用克拉尼板探索声学艺术
恩斯特·克拉德尼不仅受到罗伯特·胡克所发明乐器的启发，他也从自己的波节模式可视化实验中得到启发，发明了自己的技术来显示金属板的振动模式。
克拉尼板的工作原理
克拉尼板的形状可以是正方形、矩形和圆形，甚至还可以是小提琴或吉他的形状，只需在中心具有固定约束即可。（在克拉德尼的实验案例中，他用了一块扁平的矩形金属板，并将板的中心固定在一个坚固的底座上。）在板上撒上一种材料，比如面粉、沙子或盐，以便观察图形。（我们用沙子做实验！）接下来，在板的侧面拉小提琴的琴弓来激励板，直到它达到共振。
当板受到激励时，部分区域会振动，而另一些区域则不动。更具体地说，你可以看到沿着板的波节线的驻波。沙子从驻波振幅最大的.波腹,向驻波振幅最小的波节线 移动，形成克拉尼图形。
注意：播放此视频前请调低音量。克拉尼板发出的音符非常刺耳，算不上真正的音乐……
根据你自身的灵活程度，你可以通过采用不同的波节，在不同的波腹处用弓来激励克拉尼板，从而“播放”这块板。不同的图形会根据音调的不同而变化。
其中许多图形都非常有趣：
不同模式下同一块板上的两个克拉尼图形。
我们已经看到了克拉尼板上的图形是如何形成的，但它们又是什么意思呢？
包括克拉尼板在内的所有物体都有一套振动的固有频率。一个系统，如乐器中的驻波，往往以固有频率 或特征频率 等离散频率振动。结构以某一频率振动后，就会变形为相应的形状：特征模态。
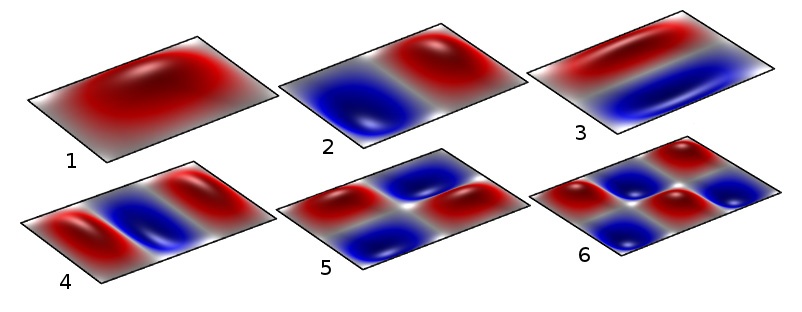
简支矩形板的前六阶特征模态。
板是一个连续系统，其特征频率取决于几何结构、材料属性和约束条件。它能表现的特征频率数量是无限的。所激励出的足以产生影响的模式尤其令人感兴趣。板的固有频率很大程度上取决于几何结构边的形状和支撑条件以及它的抗弯刚度。比如，在乐器生产中，以赫兹为单位测量的特征模态频率与木材的刚度有关。
吉他板上的克拉尼图形表示。将低频（109 Hz）下的左图与高频（426 Hz）下的右图进行比较。
通过结构力学仿真“看见”声音
声音可视化的应用领域非常广泛，例如室内家具摆放和充液管道分析。声音可视化甚至可以帮助建筑工程师设计音乐厅，使音乐厅的音响效果不会干扰小提琴演奏者对帕格尼尼第 24 随想曲的精湛演绎。通过研究声音的变化、波形、波长、速度和其他特性，我们可以更好地理解如何操纵和再现声音，以及在设计中考虑声音的物理效应。
克拉尼板模型示例。
借助结构分析软件，你可以模拟板、壳和膜中的结构振动特性——以克拉尼板为基本示例。“结构力学模块”是 COMSOL Multiphysics® 软件的附加模块，其强大的功能可供你轻松建立各种形状的板几何结构，并分析中心的固定约束。你可以从“材料库”中的内置选项中选择板材，通常是钢或铝。
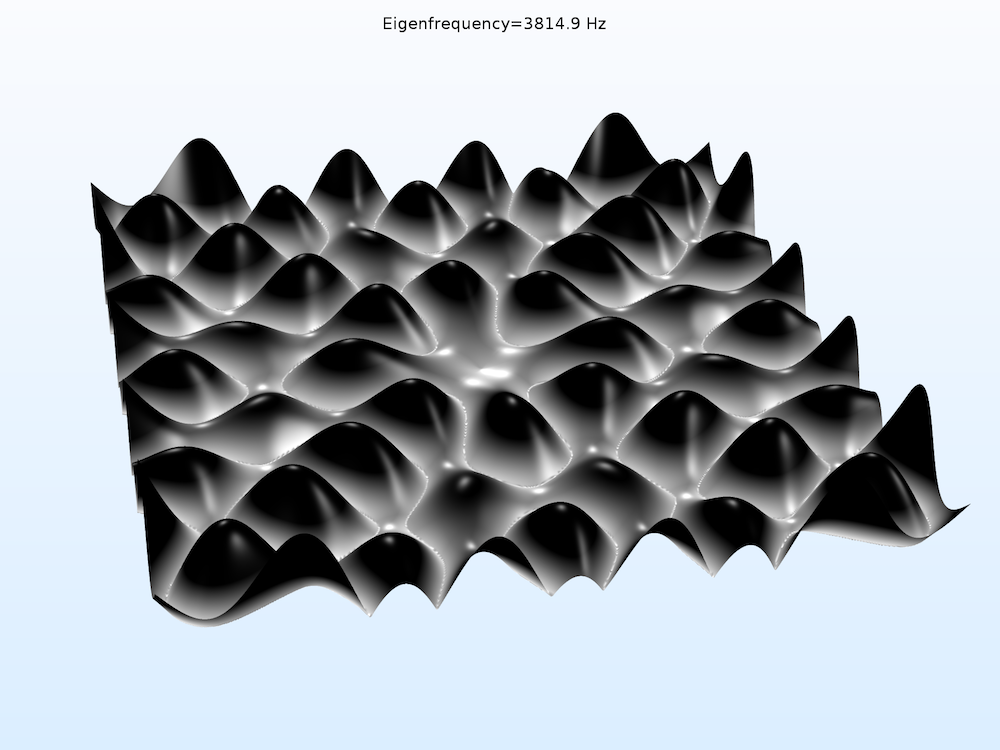
COMSOL® 软件还包含用于运行特征频率研究的预定义物理场设置。研究结果可以显示在不同频率下形成的克拉尼图形。如下所示，610 Hz 下形成的图形与 3815 Hz 下形成的图形差别非常大。你可以在涉及声音物理效应的其他设计项目中采用对克拉尼板在不同频率下的声波进行分析。
610 Hz（左）下与 3815 Hz（右）下的克拉尼仿真结果。
为了进一步扩展功能，我们可以将克拉尼板的 COMSOL Multiphysics 模型转换为一个专门的用户界面——仿真 App。为便于使用，仿真专业人员可以构建一个在仿真时对输入和输出进行限制的 App。这样，不具备仿真专业知识的人也可以将克拉尼图形可视化，并改变参数进行实验，而无需了解底层模型。
克拉尼板 App 的屏幕录像。
克拉尼板的应用不止于声音
尽管如今许多声音可视化方法已经取代了克拉尼的技术，但科研人员仍然看到了它在物理现象研究方面的潜力。例如，物理学者倾向于认为波节线的粒子运动是随机的，因而无法控制，但研究人员已经证实，可以在克拉尼板上控制多个物体的运动。一个研究小组用激光代替小提琴弓来激励刚性薄膜，观察到小的振动物体也能产生类似的效果。然后，他们通过量子点阵 将图形可视化。这一发现可能会催生出一种新型装置，该装置可帮助在设计核材料屏蔽时探测到微小的重力异常。
无论你感兴趣的是研究声波的多物理场应用，还是设计一种值得人们称赞的小提琴，都可以使用克拉尼板观察不同频率下的物理效应和不同的振动模式——从而使我们能够“看见”声音。
后续操作
自己动手做一做克拉尼图形实验。我们专门为本篇博客文章创建了一个仿真 App，你可以在“案例下载”页面获取该 App。请注意，你需要 COMSOL Access 帐户和有效的软件许可证，才能下载 App 文件。
延伸阅读
- 阅读以下博客文章，进一步了解音乐应用仿真信息：
- 阅读近来有关克拉尼板的研究：
- P.H. Tuan 等人编写的“Exploring the resonan vibration of thin plates: Reconstruction of Chladni patterns and determination of resonant wave numbers”，《美国声学学报》，2015 年，第 137 卷第 4 期第 2113–2123 页。
评论 (0)