
当结构中的应力超过可以接受的极限时,我们首先想到的是添加更多的材料来提高承载能力,这是常用的方法。但在大多数情况下,还可以考虑另一种方法,即通过去除材料来改善结构稳固性。在这篇博客中,我们介绍了一些如何通过去除材料使结构更加稳固的示例。
增加孔数
大约在 1990 年,我在为客户分析一种离心机的压力时,他们向我提出了一个问题:如何降低离心机上圆孔(这些孔的作用是喷射出分离的物质)周围的应力?我向客户建议,可以通过增加孔数来解决这个问题时(实际上也会提高生产率),他们不太能完全信服。然而,经过多次有限元分析验证后,他们对这种做法表示认可。下图所示为该离心机中孔的结构和布局:
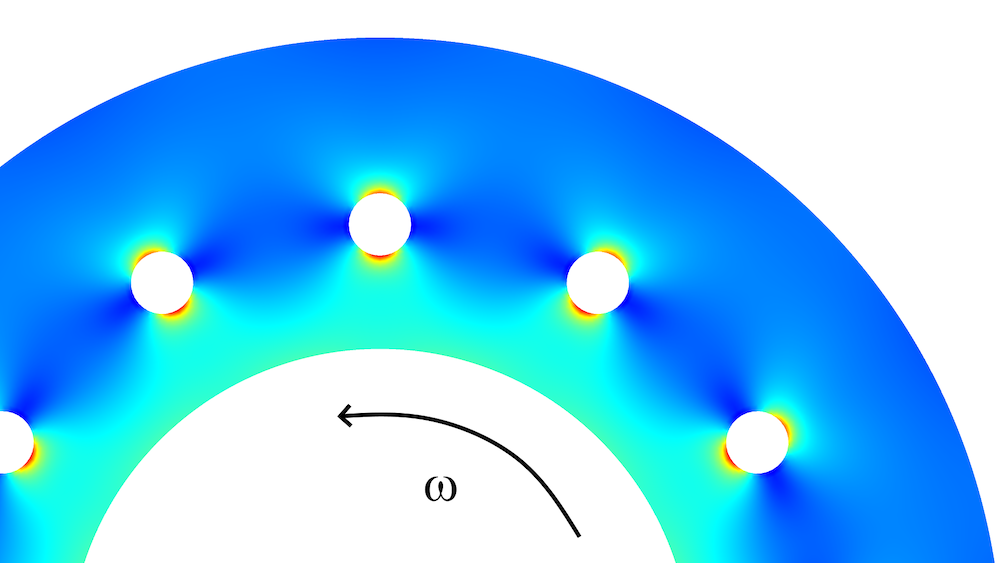
离心机的局部模拟图以及 von Mises 应力分布,其中载荷是由离心力引起的。
下图为离心机原始几何结构的局部图。图中的主应力箭头,可以帮助我们更好地了解圆孔周围实际的应力分布情况:

离心机原始几何结构中的最大主应力,圆周上有 12 个孔。
如上图所示,主应力分量沿圆周方向作用,应力流方向的改变引起应力集中。实际上,如果我们可以用圆形的狭缝代替孔,那么就不会出现应力集中。然而,这个方案行不通,因为狭缝形成的环的内部和外部几何必须连接。如果缩小孔间距,应力通量的方向改变将更少。通过手动更改参数,我们可以轻松地优化设计,找到最佳的孔分布数。实践证明,34 个孔是最佳的选择。
当离心机圆周上有 34 个孔时,von Mises 等效应力降低了 33%,同时也具有更轻的结构和更高的生产率。

带有 12 个孔和 34 个孔的离心机 von Mises 应力比较。
为什么不能让孔靠的更近呢?观察下图中的主应力分布,我们可以发现,孔与孔之间的连接部位会受到离心力引起的径向应力,因此孔间距不能太小。

带 34 个孔的离心机上的最大主应力。
圆角设计
在几何形状突然发生变化的地方,通常会产生应力集中。经验丰富的设计师会采用比较缓和的设计进行平缓过渡,并使用较大的圆角半径。但是,增加圆角半径可能不可行,因为添加的材料会干扰其他零件。
此时,我们可以采用 底切 或 释放槽 设计,通过去除材料来增加半径。(请注意,在焊接中,底切 通常是指某种类型的焊缝缺陷。)
下文,我们列举了三种不同的设计方案。在原设计(顶部)中,应力集中系数为 1.91。通过将圆角半径增加 50%,可以将应力集中系数降低 13% 至 1.67。红色虚线右侧较薄的部分厚度保持不变,因此,增加圆角半径会损失一些空间。
第三种设计采用了较大的底切半径。这也可以使应力集中降低 13%,但不会使空间变小。采用底切设计的缺点是零件的制造可能更加复杂,因此价格昂贵。
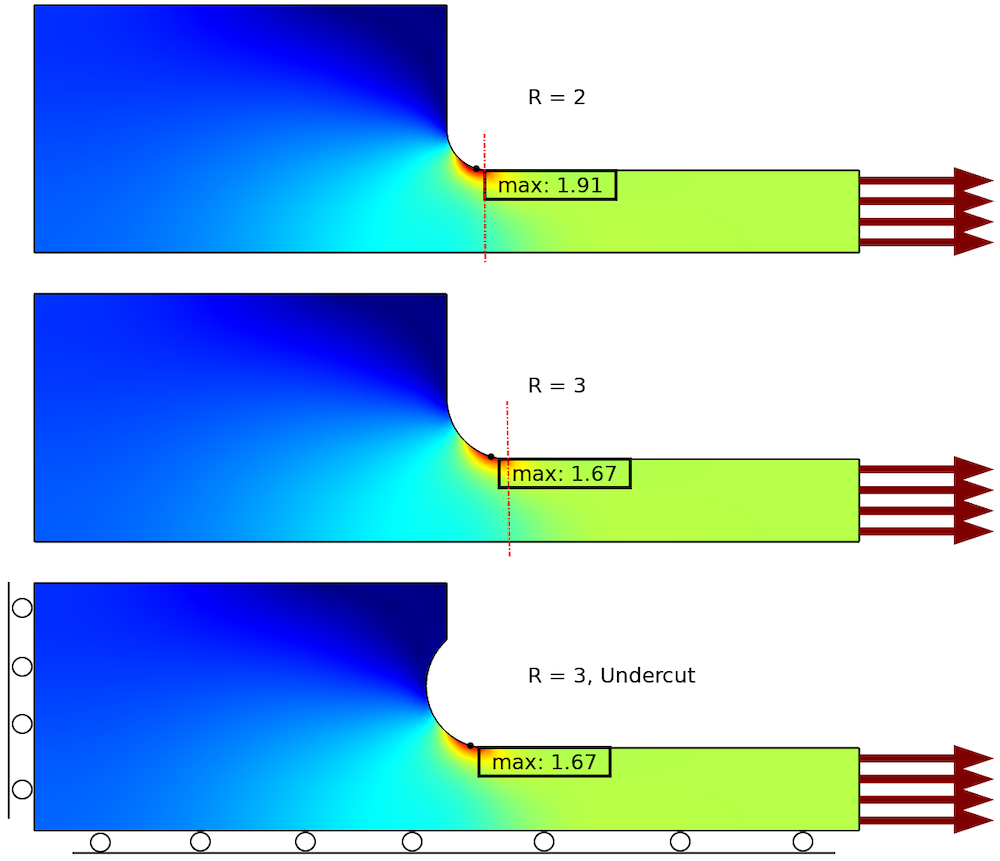
使用两种不同的几何设计降低应力集中。
焊接的应力释放槽设计是一个特殊的例子。由于焊缝对疲劳非常敏感,因此可以通过在焊缝前面添加凹槽进行保护。实际上,由于疲劳强度不同,在凹槽处产生的应力可能比焊趾处更高。
控制位移
当结构上的载荷由受控位移而不是指定的力组成时,添加更多的材料通常只会使载荷增加,而应力恒定或者增加。大多数情况下,刚开始似乎并没有控制位移,但实际上是被控制的。热变形是一个指定位移的示例。
以下图所示的 2D 几何模型为例:
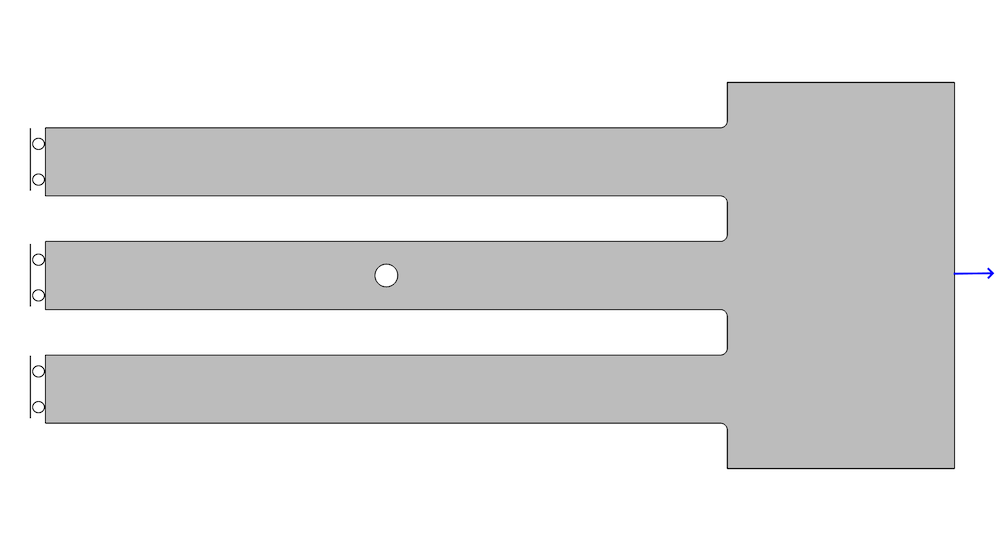
几何和边界条件
将三个杆向右侧拉伸 0.1 mm,在模型的左侧,假设有一个对称面。应力分布结果如下图所示。
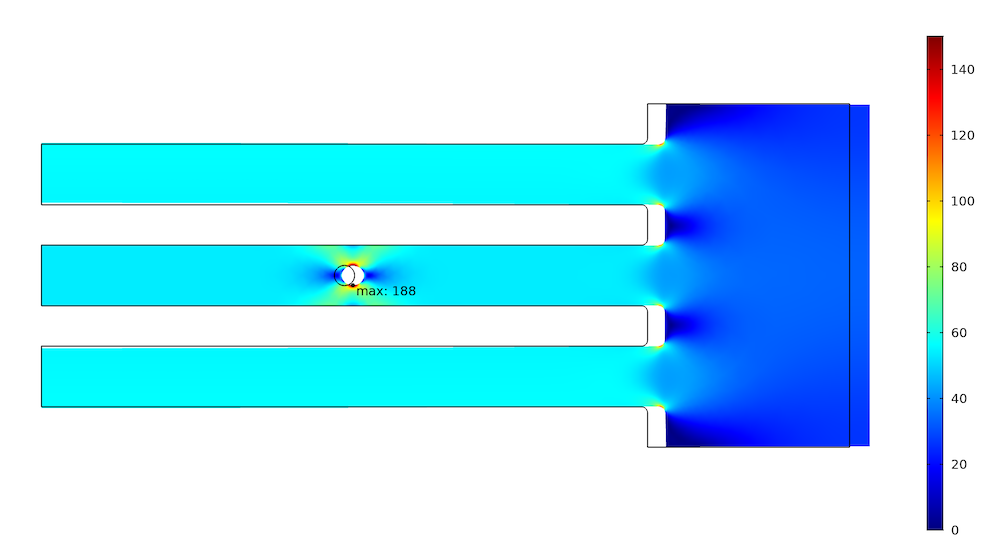
指定位移时的应力分布(变形放大 100 倍)。
上图中,圆孔处的最大应力为 188 MPa,外部两个杆上的载荷为 3.36 kN,中间一个杆的载荷为 3.22 kN。现在,我们可以尝试通过减小材料刚度来降低载荷和中心杆的应力。当然,这可以通过许多不同的几何变化来实现,但因结构功能限制而选择度较小。在这个示例中,我们可以在对称面上制作一个半径较大的凹槽进行对比,如下图所示。
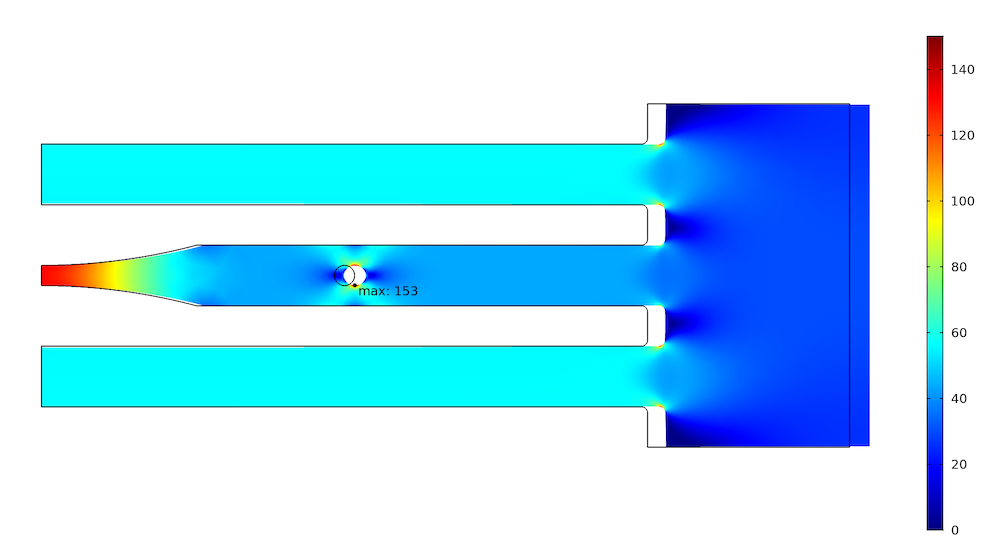
这样做可以将最大应力降低 19% 至 153 MPa。很显然,去除更多的材料可以减少更多的应力。
其他两个杆上的应力发生了什么变化?由于是指定位移,因此杆不会被拉长。杆上的应力实际上增加了不到 1%,为 3.36 kN;由于指定的位移不是直接施加到杆上,而是通过一个有弹性但坚硬的结构施加的,因此杆上的应力略有增加。真实的结构中往往就是这种情况。
更改加载路径
仍以上述几何模型为例,我们对结构施加力载荷。设定载荷大小为 9.94 kN,使其完全等于由指定位移引起的反作用力;显然,在原几何模型中,应力大小一致。
但是,当我们减小中间杆的刚度时,两个外侧杆必须承担更多的载荷。而且,由于结构的总刚度降低,在载荷边界处的位移必须有所增加。
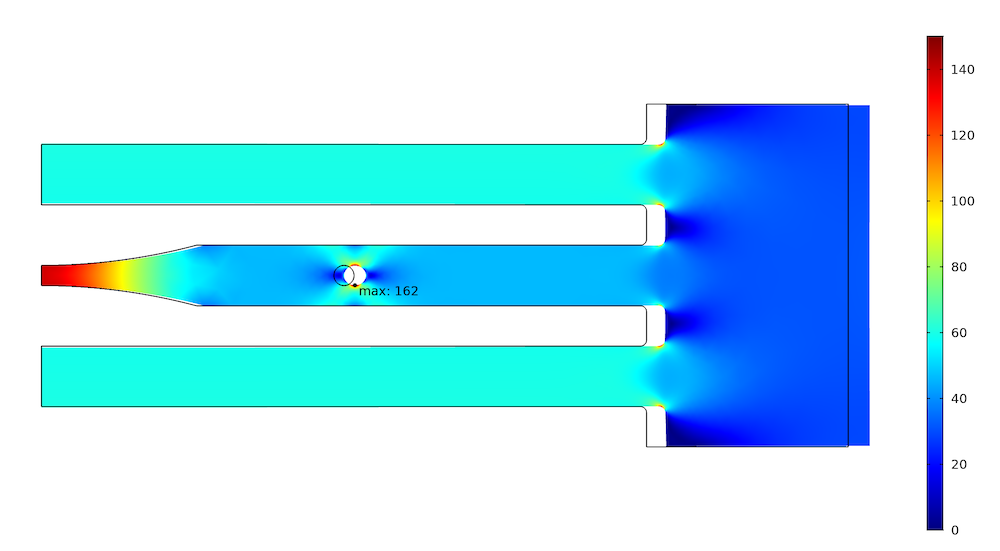
当施加力时,刚度较低的结构中的应力分布。
可以看出,最大应力减小较少。外部杆的载荷已增加到 3.58 kN,而中间杆的载荷则为 2.77 kN。
指定载荷是通过将力传递给其他部件来减小关键部件中的力,其机制与指定位移(更改加载路径)完全不同。还有一个更简单的方法也可以更改加载路径,即通过增加 2 个外杆的厚度。但这不是本文的研究内容,这属于添加材料而不是删除材料。
如何使结构更加稳固?
由上述示例可以看出,大多情况下,去除材料有助于降低局部应力水平,但同时也会增加制造难度。
对于上述示例,我们可以根据工程师的直觉来改变结构,但使用参数、形状或拓扑优化等方法,可以获得更好的结果。对于复杂的几何结构,可以通过增材制造方法来制造。
请点击下面按钮,了解更多有关 COMSOL® 软件的力学分析功能。



评论 (0)