
在开发一个新产品或新功能时,第一步通常是单独了解功能特性。要通过数学建模获得可靠和准确的预测,必须非常详细地指定关键组件、测试设置和边界条件。然而,大多数工程师更愿意关注关键组件,而不是 “不相关”的部分。COMSOL Multiphysics 声学模块中新增的阻抗边界条件可以帮助工程师更准确地指定边界条件。
什么是阻抗边界条件?
在回答上述问题之前,我们先来看看边界条件的定义。引入边界条件意味着 “我们知道在特定的边界上会发生什么”。边界条件会为域内正在求解的控制方程的动力学施加一个额外的约束。这个约束可以是一个已知的振动速度、一个硬声场壁或一个对称平面。施加了额外约束后,COMSOL Multiphysics 会寻找满足声学动力学 和 边界条件的解。
阻抗模型实际上是 “全流动”的模型,即同时对声压和声速施加一个条件,用于定义这两个因素之间的特定关系。在一些理想的情况下,这种关系是已知的。引入一个阻抗条件,本质上是形成一个特定的理想的声学行为。因此,阻抗边界条件 是一个很强大但简单的条件,适用于理想化动力学存在较明显的情况。例如我们熟知的麦克风腔的膜动力学,长管道中的声学,以及多孔表面的平面波声学,等等。
在数学上,阻抗边界条件指定了压力 p 和速度 v 之间的线性关系。
(1)
式中,Z_\textrm{s} 是包含动力学的阻抗(SI 单位:Pa*s/m)。最高级的阻抗模型是在频域中给出的。因此,Z_\textrm{s} 通常是一个与频率有关的参数,Z_\textrm{s}=Z_\textrm{s}(\omega)。
与其指定一个 比阻抗 将速度与每一个点的压力联系起来(如等式(1)),不如使用声学阻抗 Z(SI 单位:Pa*s/m^3)将作用在一个表面的压力与该表面的体积流量 Q 相关联,即
(2)
最后,我们得到为行波定义的 特征比阻抗Z_\textrm{c}。这类阻抗与波在域中移动时每一点的粒子速度和压力有关,这使它们成为对无限域有用的低阶模型。平面行波的关系,Z_\textrm{c}=\rho c 就是有一个典型的例子。
声学模块中的新阻抗模型
COMSOL Multiphysics 声学模块中的阻抗边界条件内置了几个直接可用于一系列声学应用的新模型。所有新增的模型都包含频率依赖性,并且只在频域中可用。(如果要在时域中定义一个阻抗边界条件,可以使用 用户定义的阻抗 边界条件)下表对这些模型进行了简单的描述,包括 压力声学 物理场接口的 阻抗 边界条件下的新增模型。
| 名称 | 描述 | 应用 |
|---|---|---|
| RCL | 集总参数电路元件模型,允许声阻(R)、声顺(C)和声惯(L)的任何组合。 |
电声: 用于移动设备和消费电子产品的麦克风膜、传感器等模型。
声-固相互作用:弹性材料和固体的机械行为的简单模型。 |
| 生理学 | 经过实验验证的人耳和皮肤的模型。 |
助听器:人耳内使用的助听器的适当边界条件。 头部设备、移动设备、耳机:消费类设备的工作条件的理想声载荷。 人的皮肤: 人体是模拟域的一部分的模拟。 |
| 波导末端阻抗 | 波导两端的声学模型,有法兰盘和非法兰盘配置的选择。 | 长管道和导管:用于在管道和导管末端截断模拟域。当传播的波是平面波时,阻抗边界条件是很好的近似值。 |
| 多孔层 | 背部是硬壁的多孔材料层上的法向入射声学的通用模型。 | 室内声学: 带有吸声层的室内声学模拟的简单边界条件。 |
| 特征性的特定阻抗 | 无限域的平面波、圆柱波和球面波的行波声学的理想化模型 | 无限域: 无限域的原始模型,假设感兴趣的区域的声辐射可以充分地近似为平面波、圆柱波或球面波。辐射边界条件的使用性更广。 |
如下面的屏幕截图所示,在阻抗模型阵列之间转换是非常容易的。对于更复杂的选项,我们使用了一个插图来进行详细的描述。
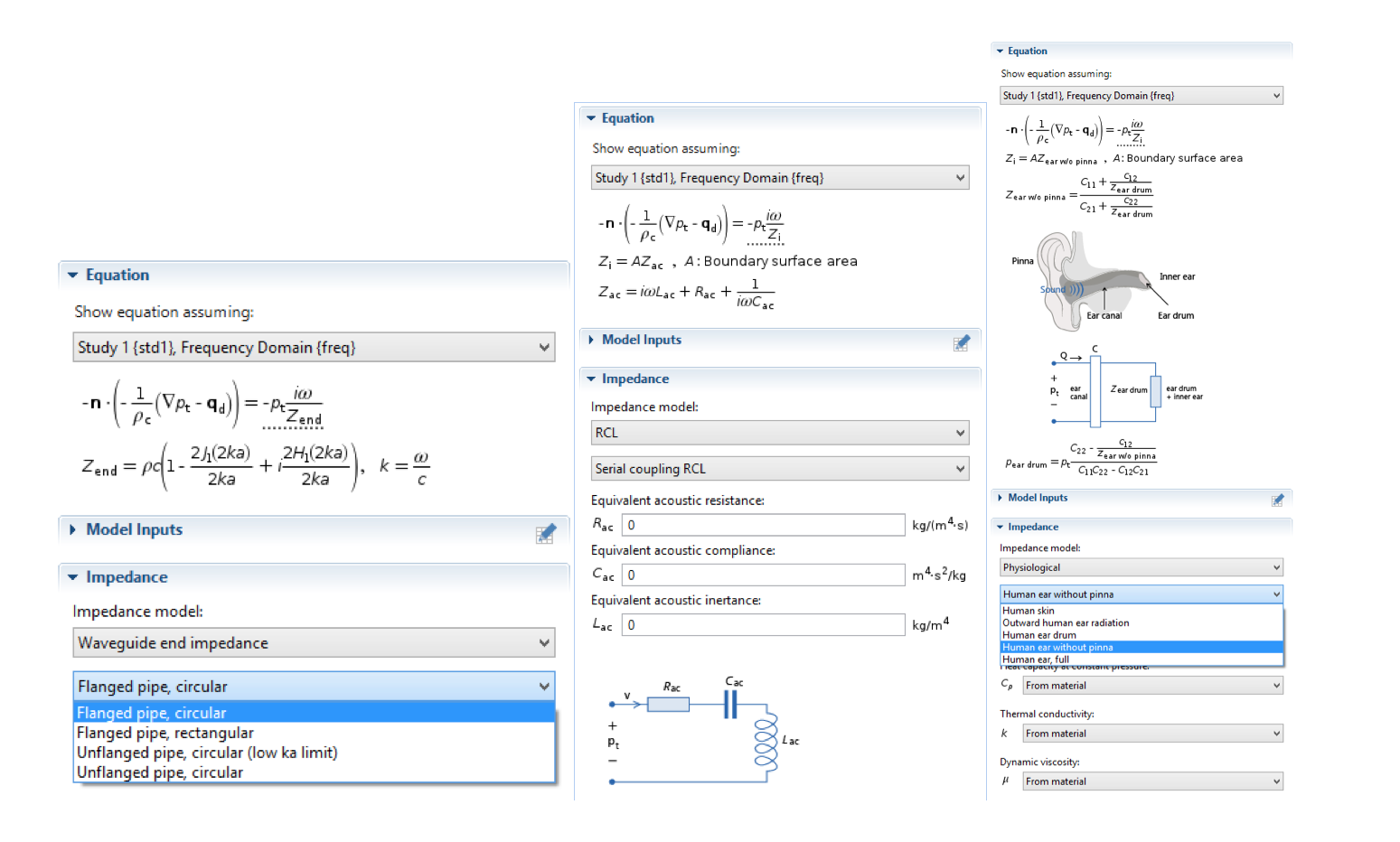
一些阻抗模型的用户界面(UI),包括法兰管模型,圆形模型;串联耦合 RCL 模型和无耳廓人耳模型。
在声学仿真中使用阻抗边界条件
接下来,我们将通过几个例子来展示如何利用阻抗边界条件中的 RCL 功能选项。第一个模型侧重于使用 RCL 电路表示一个测量传声器。后面两个例子是基于同一个系统的,复杂的 COMSOL Multiphysics 模型被当作一个“实验”,其中某些部分(一个子模型)可以通过阻抗进行参数化。在第一个例子中,阻抗是作为一个插值函数给出的。在第二个例子中,使用优化的方法将一个 RCL 模型拟合到了数据上。
电声学的 RCL 条件
我们可以首先考虑一种情况,即阻抗边界条件的参数是已知的。这种情况在电声学中很常见,因为经常要为设备指定集总参数值。
在许多工程领域,包括声学领域,集总参数建模是公认的建立无空间分辨率的有用模型的策略。在新的阻抗边界条件中,RCL选项下有一个简单的集总参数模型的一般框架。我们以一个简单的麦克风例子来说明,比如集总接收器教程中所演示的那样。在这个案例中,我们分析了一个接收器(微型扬声器)的行为,在另一端放置了一个麦克风用于读出信号。
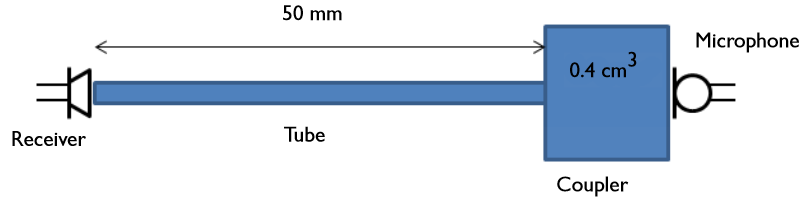
放在测试装置中的接收器(微型扬声器)的几何模型。
为了模拟传声器,我们使用一个串联 RCL 阻抗条件
(3)
式中,C 是传声器的声顺(衡量膜被推回时后面的空气量),R 是系统损耗(热黏性阻尼),L 是膜的声学质量。该条件被均匀地应用在出口的整个端部,隐式忽略了如果包括一个完整的传声器模型,在不同径向坐标上的振膜位移变化。
与实验测量相比,该模型使用等式(3)中的简单边界条件出色预测了传声器宽频带。阻抗提供了一个具有足够真实动态的边界条件,使我们可以将重点放在接收器和其他单元的详细建模上。
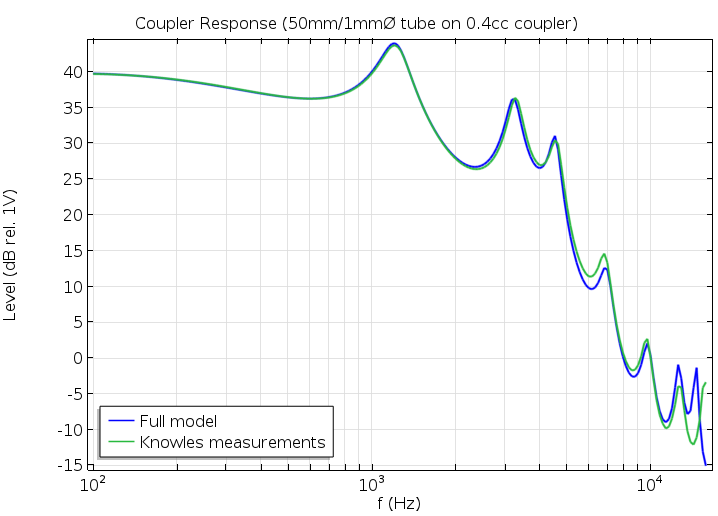
耦合器区域内的压力比较图。
如何使用阻抗对子组件进行建模
换个角度,我们现在来看看如何提取一个阻抗模型,用于表示一个复杂的子组件。你可以在 COMSOL 案例下载页面下载将要介绍的模型。
此案例模型包含一个简单的类似消声器的系统(也可以是消声器的一部分),由一个长管道和一个二维轴对称亥姆霍兹共振器组成(见下图)。振幅为 p_\textrm{in} 的平面波在入口处入射,在入口和出口处应用辐射条件。亥姆霍兹谐振器的狭窄颈部存在明显的黏热阻尼。由于存在这种损耗,仅使用 压力声学 接口是不够的,建立完整的模型需要在该区域使用 热声学 接口。在管道的主要部分,使用 压力声学 接口就足够了。该模型使用了 压力声学 和 热声学 接口,以及 声学-热声学 边界多物理场耦合。
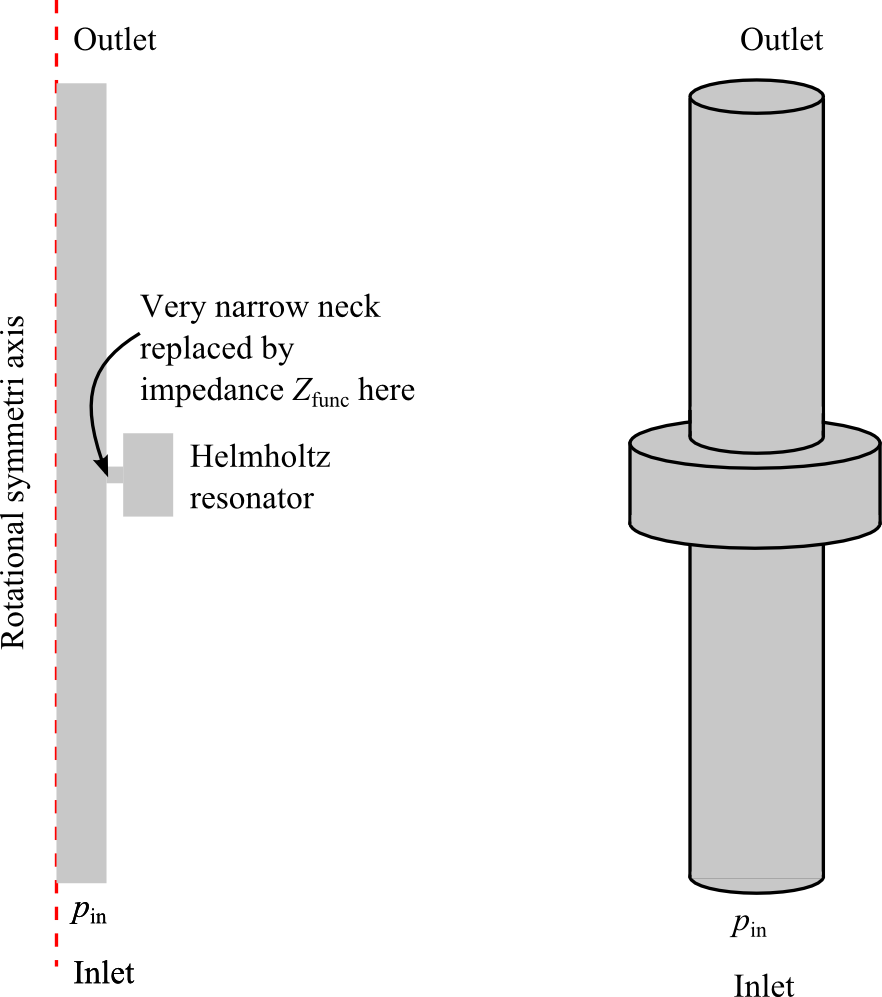
带亥姆霍兹共振器的类似消声器的系统。左边的示意图对应于 COMSOL Multiphysics 中实现的二维轴对称几何结构。注意进入谐振器的非常狭窄的颈部,主要产生黏性热损耗。
由内插函数计算用户定义的阻抗
当从组件仿真转移到系统仿真时,将某些组件或全组部件集总在一起可能是有利的(即,求解当前谐振器中的热声模型在计算上很昂贵)。为此,我们可以用一个阻抗边界条件取代 热声学 子模型(亥姆霍兹谐振器),将该条件应用于颈部进气口所在的区域。这样一来,就可以只用 压力声学 接口模拟整个模型。
首先,从完整模型中提取颈部的有效阻抗 Z_{\textrm{func}}。计算平均入口压力与平均入口速度的比率,即
(4)
下图说明了 Z_{\textrm{func}} 的实部和虚部。这些数据用于为 Z_{\textrm{func}} 创建两个插值函数:一个用于实部(Zfunc_real),一个用于虚部(Zfunc_imag)。这些函数包含了所有关于阻抗的信息,可以在 用户定义 的阻抗边界条件中通过书写: Zfunc_real(freq)+i*Zfunc_imag(freq) 调用。利用这个阻抗,我们仅使用 压力声学 接口建立了一个简化的模型。亥姆霍兹共振器不再包含在设置中,但它是用阻抗来表示的。
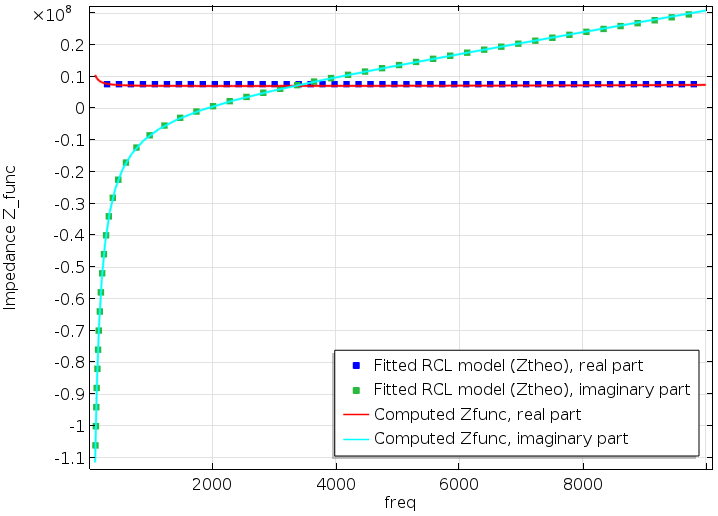
共振器阻抗 Z_{\textrm{func}},通过等式(4)从全耦合模型中获得。这些点表示等式(6) 与实线所给数据的最佳拟合。
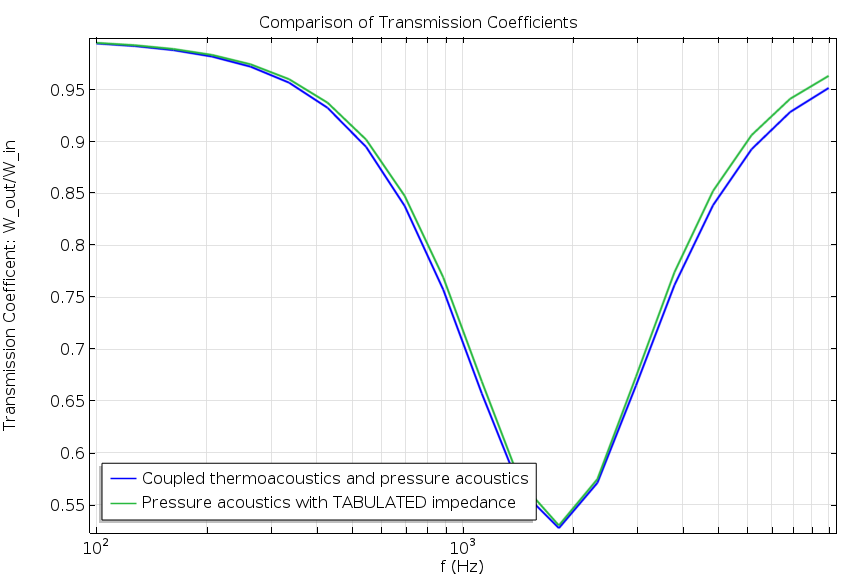
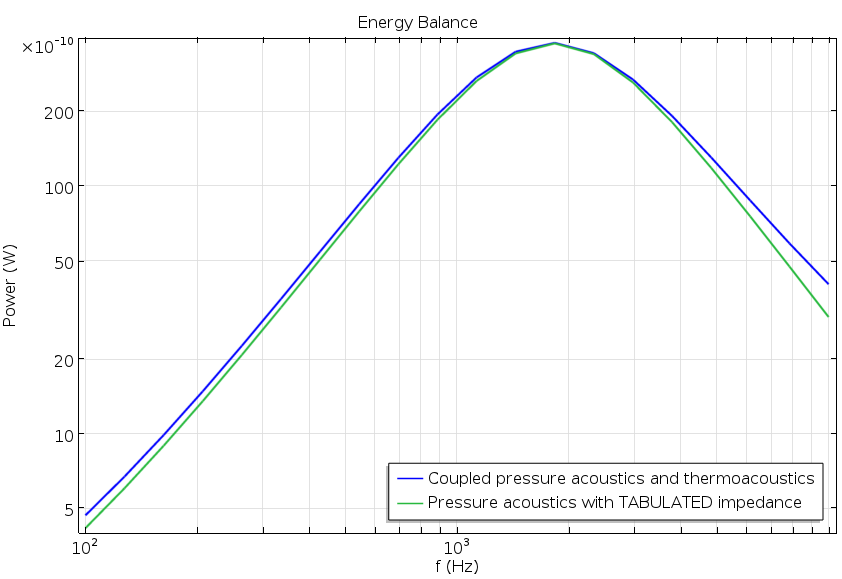
为了评估简化模型的性能,我们计算了整个主管的 透射系数\tau。透射系数的定义为透射功率 (W_{\textrm{out}}) 与入射口功率 (W_{\textrm{in}}) 的比率。我们还绘制了“能量平衡”,即系统中耗散的能量。它可以由入射功率与反射功率和透射功率之差表示
(5)
式中,W_{\textrm{ref}} 是反射功率。
下面两幅图对结果进行了描述。两幅图都显示出良好的一致性,完整模型和使用内插阻抗的简化模型之间几乎没有差别。一个额外的好处是求解时间更短了,因为简化模型只需要 3s 就能求解(全耦合模型需要 25s)。虽然这些数字取决于硬件,但确实反映了去除需要求解谐振器中热声模型后,计算效率的提高。
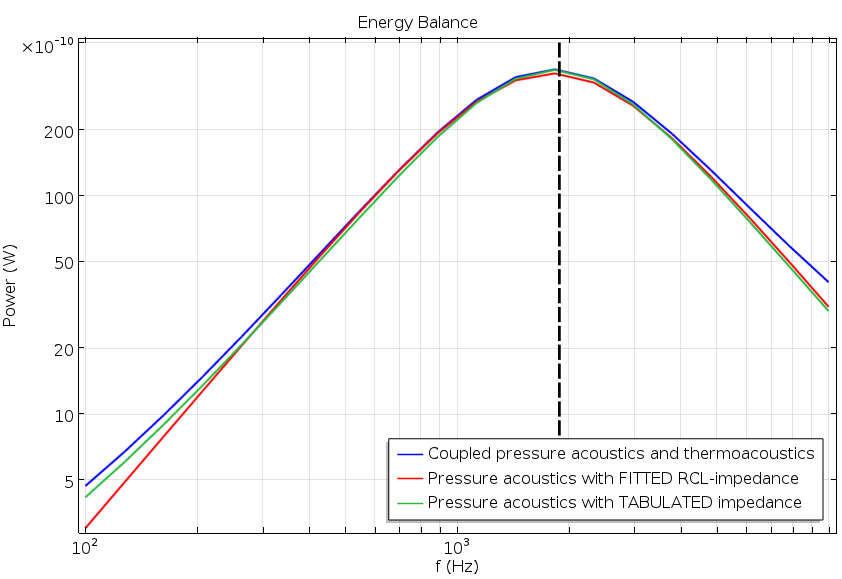
透射系数图(左)和显示耗散能量的能量平衡图(右)。
然而,在大多数实际情况下,首先求解一个复杂的模型,然后再将它简化并不是特别有利。可以对单个子组件单独建模并进行表征。从完整模型得出的复杂子组件的详细阻抗模型应保存在一个库中,必要时可以调用。COMSOL Multiphysics 具有支持这种做法的功能:复杂子组件的结果的表格值可以保存到文件中,并在需要时调用。
使用优化技术的拟合 RCL 模型
在使用先验 知识推导出阻抗的数学形式的情况下,或者当数据明显适合于简单的数学形式时,首选的方法可能是将一个简单的理论模型与完整详细的 COMSOL 模型相匹配。对于前一种情况,阻抗模型的参数值反映了底层物理场的特征,并提供了对系统的洞察力。例如,如果可以使用RCL类型的模型很好地描述数据,如使用等式(3),就可以立即得到共振频率。
下面,我们将对理论模型与阻抗边界条件的拟合步骤进行说明。亥姆霍兹谐振器有一个移动的声学质量(颈部的空气),一个声顺(谐振器体积内的可压缩空气),以及损失(热黏性损失)。因此,在整个频率范围内,一个好的模型是
(6)
其中,R_{\textrm{func}}, C_{\textrm{func}} 和 L_{\textrm{func}} 是要拟合的未知参数。使用优化模块,通过目标函数 \left| \left( Z_{\textrm{theo}}- Z_{\textrm{func}} \right)^2 \right| 将等式(6) 与 Z_{\textrm{func}} 进行最佳拟合,得到以下拟合参数值
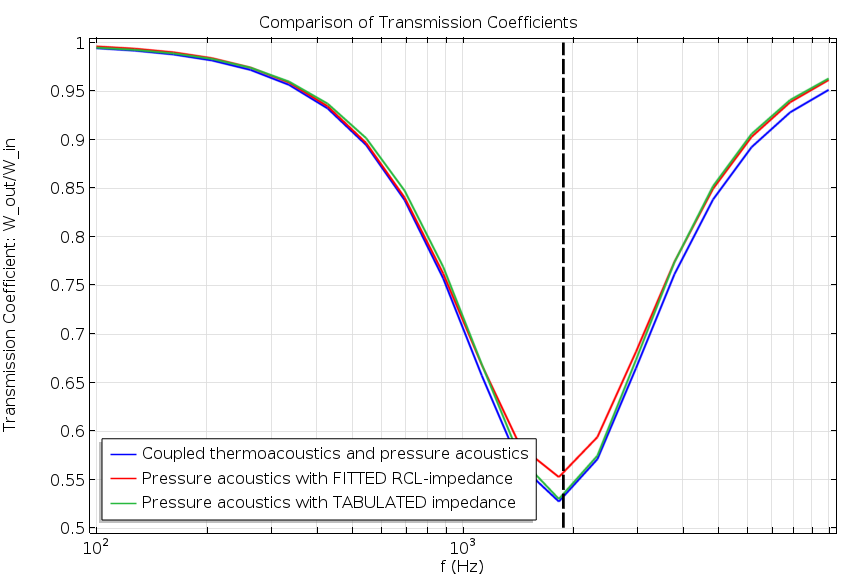
这些值是通过 RCL 选项直接输入到阻抗边界条件中的。(对于一般的理论模型,可以使用 用户定义 选项,因为它接受任何模型,无论其复杂程度如何)。只使用 压力声学 接口和 RCL 阻抗模型,我们再次比较了新的简化模型和全耦合模型的结果。我们绘制了透射系数 \tau 和等式(5)的能量平衡。
透射系数(左)和能量平衡(右)图。显示了简化模型(红色)、全阻抗模型(绿色)和全耦合模型(蓝色)的结果。后两个结果是在前面这个图中展示的。
我们再次观察到,在整个频率范围内,两个指标都有良好的一致性。与最初的例子相比,高频响应对全耦合模型的表现略好,而低频的情况则相反。
如前所述,我们现在可以使用简单的边界阻抗模型来更深入地了解系统。现在,让我们把这种方法应用到一个简单消声器模型中。
像等式(6)这样的串联耦合 RCL 模型的谐振频率,可以由 f_{\textrm{res}}=\frac{1}{2 \pi \sqrt{C_{\textrm{func}} L_{\textrm{func}}}} 计算。因此,预计最佳的消声器工作条件(最低传输系数)将在以下频率实现
事实上,情况确实如此。虚线表示上图中的谐振频率,很好地预测了最小透射系数。
如果您有任何问题,请联系我们。






评论 (0)