最新内容

使用 COMSOL 理解稳定性方法
2014年 5月 30日
在这里,我们提供了一个质量传输示例模型,以帮助描述稳定方法对您的数值模型的影响。

变形固体中的传热仿真
2014年 5月 28日
在之前的文章中,我们介绍了一些涉及静止固体耦合传热的应用。这些静止固体传热示例对将要求解的传热方程进行了简化处理,并且通常可以得到求解温度场的精确近似。当涉及传热和固体力学的多物理场耦合时,如何描述用于解释材料热弹性效应的相关物理场?

地热能:利用地热实现冬暖夏凉
2014年 5月 23日
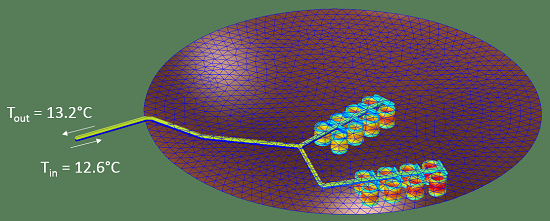
利用地热调节室内温度具有成本低、可持续使用的特点。本文为地热能系列的第三篇博客文章,我们将详细探讨埋管集热器。由于对埋管集热器的热性能已做了准确预测,并且考虑了管道布置与局部热性质,因此“管道流模块”非常适合模拟这种集热器。

射频加热和微波加热模拟快速入门
2014年 5月 20日
在射频加热和微波加热网络研讨会中我们经常演示波导模型,因为使用它阐述概念人们比较容易理解。这里,我们再次将其作为模拟射频加热和微波加热的快速入门。

非线性材料的热疲劳建模
2014年 5月 1日
在模拟非线性材料的疲劳时,有两个挑战。1.) 正确地表示材料的行为;2.)找到一个能够捕捉到寿命控制机制的疲劳模型。
如何在不知道积分限的情况下对函数进行积分?
2014年 4月 30日
您知道 COMSOL® 软件可以解决积分和偏微分方程吗?学习如何积分函数——即使不知道积分的极限。

弱形式的力量
2014年 4月 29日
如果你正在使用有限元仿真软件(例如 COMSOL Multiphysics),就会在某些时候遇到“弱形式”这一表述。这个时候,你可能会想知道这个表达是什么意思?实际上,弱形式是一个非常强大的概念。

传热与地下多孔介质流的耦合仿真
2014年 4月 24日
本文为地热能系列博客的第二篇,将重点探讨传热与地下水流耦合的过程,并据此确定地下储藏的热量是否足够多,以及是否值得开采获得地热能。文中,我们将通过一个地下水换热回灌系统示例模型演示这一耦合过程。



