
在模拟主要由对流而非扩散驱动的传递应用时,大多数数值模拟方法(有限元、有限体积和有限差分)需要 稳定性方法。对于有限元法 (FEM),稳定性意味着引入少量人工扩散项,这将带来更稳健和更快的计算性能。今天这篇博文,我们将介绍关于稳定性对您的数值模型的影响的一些见解。另外,我们还研究了一种非常有效且不需要任何稳定性的替代数值方法。
什么时候需要稳定?
COMSOL Multiphysics 使用有限元法(FEM),一种众所周知的成熟方法,来数值求解控制偏微分方程 (PDEs)。在解决由扩散驱动的固体力学应用或传递现象时,该方法很简单。然而,对于以对流为主的传递问题,大家都知道,这种方法会导致数值不稳定性,即解的振荡。COMSOL Multiphysics 会自动使用稳定方法来防止这种现象。尽管如此,一些知识对于理解传质模拟的性能确实很有帮助。
未知溶液 u 的一般对流扩散传递方程为:
参数 \beta 和 c 分别指对流速度矢量和扩散系数,而 F 表示任意源项。该方程可以表示能量方程,即传热方程、质量传递方程(用于化学物质的传递)、用于流体中动量传递的 Navier-Stokes 方程或任何其他传递方程。对于具有一阶形状函数的均匀网格,已被证明当 Péclet 单元数 \mathrm{Pe} 超过 1 时,会发生数值不稳定:
其中,h 为网格单元尺寸。
Péclet 单元数与对流和扩散效应有关。无论是大的对流或小的扩散活动都会导致 Péclet 数大于 1。但这只有一半是正确,因为网格元大小也起着重要作用。网格分辨率越高, Péclet 单元数越小。这也意味着对于每个非零扩散项,都存在一个网格分辨率,迫使整个计算域中的Péclet 单元数小于 1。
然而,这样的网格在计算上很昂贵,甚至不可行。稳定方法允许在更粗的网格上进行模拟,从而大大减少了计算负荷。
一个质量传递的例子
为了更好地理解稳定方法的效果,我们来看一个示例并使用 COMSOL Multiphysics 对其进行求解。我们考虑一个瞬态传质问题。假设有一个三米长的管道,其中有一个平推流(在管道横截面上以恒定速度流动)。平推流的速度为 1 m/s。在实验开始时(即在 t = 0 时),一种化学物质以如下浓度溶解在水中:
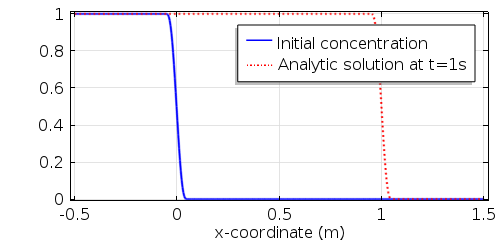
在 x=1m 时,将初始浓度(蓝色部分)设置为 1。这张图还显示了 t=1s 时浓度的解析解。因为流体速度是 1m/s,浓度不连续点应该位于 x=1m 处。接下来,我们的目标是找出浓度分布随时间的变化。
我们可以在 COMSOL Multiphysics 中使用 稀物质传递 物理场接口对这个问题进行一维建模。在这个物理场接口中,我们计算在对流和扩散的驱动下化学物质浓度随时间的变化。其中,速度被设置为 \beta=1~\mathrm{m/s} ,扩散系数为 c=10^{-9} ~\mathrm{m^2/s}。
在入口处,我们将浓度设定为 1~\mathrm{mol/m^3}. 网格大小设定为 \Delta x=0.05, 得到 Péclet 单元数约为 25\cdot106,远远超过临界值 1。在运行瞬态求解器到 t=1s 后,将获得以下解(蓝色实线)而无需 稳定性。为了进行比较,我们还显示了解析解(红色虚线)。
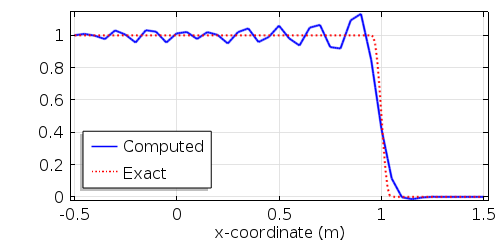
我们可以清楚地看到,计算解是无用的。振荡不仅存在于浓度梯度周围,而且分布在整个域中。当 Péclet 数超过 1,并且存在下列任何条件时,就会发生这些振荡:
- 一个与空间相关的初始条件,网格无法求解
- 狄利克雷边界条件导致在边界附近有一个陡峭的梯度并形成边界层的解
- 接近非恒定源项或非恒定狄利克雷边界条件的小的初始扩散项
这个质量传递的例子说明了第一点,因为我们选择了一个与空间相关的初始浓度分布。我们可以确定迫使 Péclet 数小于 1 的网格单元大小:
对于整个域来说,如此小的网格单元将导致需要构建超过 10 亿个单元,这应该足以成为我们考虑不同选择的动力。
使用 COMSOL Multiphysics 实现稳定性
所有传递接口,例如传热、流体流动或物质传递,都会自动使用稳定性。为了看到相应的设置,我们首先需要通过单击模型开发器上方的眼睛符号来打开“稳定性”。在物理场节点中,我们将找到两个附加部分,即“自洽稳定性”和“非自洽稳定性”,如 稀释物质传递 接口的屏幕截图所示:
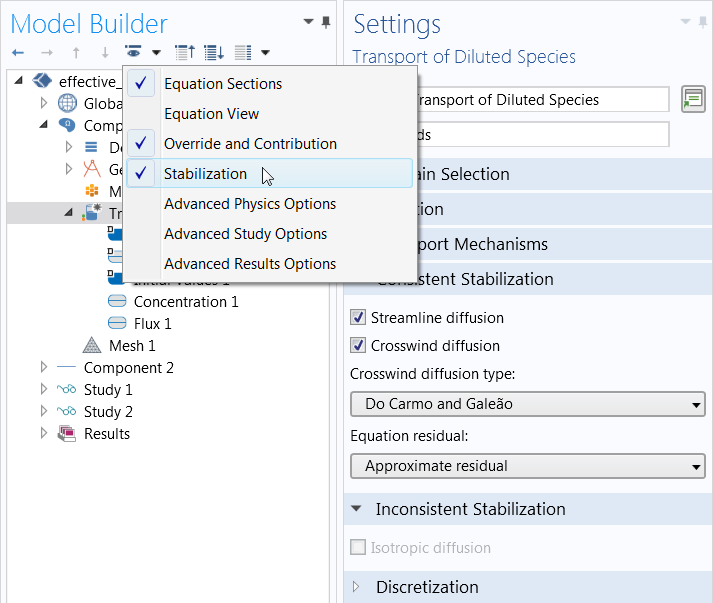
如何使稳定设置可见。
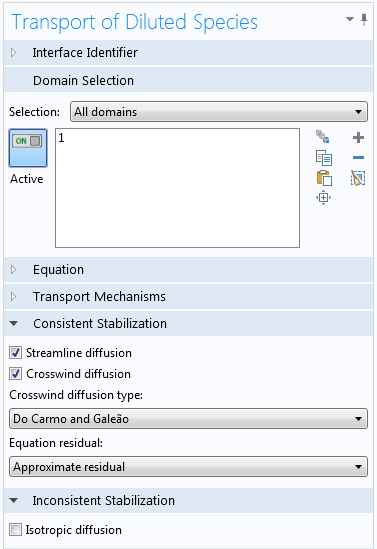
稀物质传递接口的稳定性设置。
默认情况下,会检查自洽稳定性,因为这个方法适合大多数应用程序。
在下一节中,我们将简要地解释这两种方法的思想,并给出质量传递实例的相应结果。所有稳定方法的主要思想是通过增加额外的扩散项,来减少 Péclet 数。虽然这听起来很简单,但这种额外扩散的引入可以通过许多不同的方式实现。
非自洽稳定性:各向同性扩散
最简单的方法是定义一个人工扩散系数 c_{\mathrm{art}},即:
并将其添加到物理扩散系数 c 中,给出一个整体扩散系数 c+c_{\mathrm{art}}。参数 \delta 是一个调谐参数,通过它可以调整人工扩散的量。相应的Péclet 单元数由下式给出:
为了确保 Péclet 数不超过 1,需要一个调整参数 \delta=0.5。实际上,较小的值通常足以稳定计算。这就是为什么 COMSOL 软件建议您使用 \delta=0.25。由于这个方法增加了所有方向的扩散,因此将其表示为 各向同性扩散。它被称为非自洽,因为它增加了一定量的扩散,而与数值解与精确解的接近程度无关。
需要注意的是,人工扩散的量取决于网格单元的大小。一方面,高分辨率网格意味着更少的 各向同性扩散,但是会有更多的计算工作。另一方面,允许较粗的网格需要更多的 各向同性扩散,并且会显著影响解。我们需要在准确性和努力之间找到一个平衡。
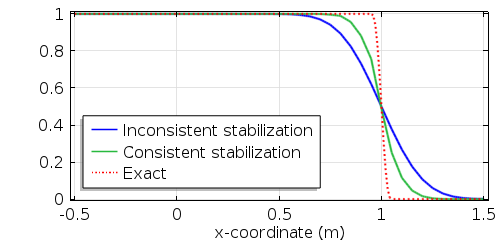
t=1 时的浓度分布比较表明,对于相同的网格 (\Delta x=0.05),非自洽稳定(蓝线)比自洽稳定(绿线)引入了更多的扩散。这就是为什么自洽稳定是所有传递物理场接口的默认选择的原因。这也是我们接下来要讨论的内容。
自洽稳定性:流线和侧风扩散
与非自洽方法不同,自洽方法给出的数值扩散越小,数值解越接近精确解。换句话说,就是在网格足够细的区域没有添加扩散。
提示:你可以在 COMSOL Multiphysics 参考手册中阅读更多的数学解释和参考资料。
流线扩散法只在流线方向增加扩散,也称为迎风。如下图所示,这种方法通常可以避免放大振荡(蓝线),但陡峭的梯度仍然会导致局部扰动(称为过冲或下冲)。为了克服这个问题,我们还使用了侧风扩散。
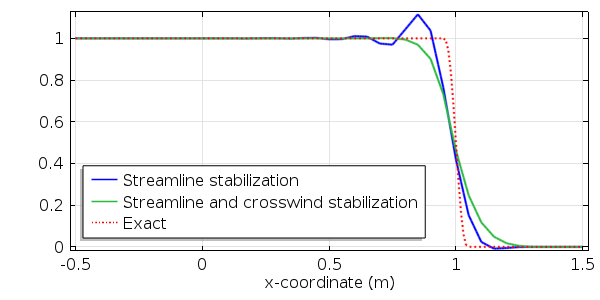
侧风稳定性(绿线)不仅增加了横向的扩散,还捕获了不连续性,因此消除了数值下冲和过冲。自洽稳定方法(流线与侧风稳定)通常更有效,因为与非自洽稳定相比,增加网格分辨率可以更快地收敛到精确解。反过来,这意味着找到物理上可接受的解决方案需要更少的计算工作和时间。
上图显示自洽稳定性消除了接近突变浓度梯度的所有振荡和数值过冲或下冲。然而,结果与解析解相差甚远。这是因为与初始浓度分布 (\Delta transition=0.1) 中的过渡区域的网格尺寸相比,网格非常粗(\Delta x=0.05),以及使用一阶元素的事实。下一个结果表明,当我们细化网格时,解会收敛并到精确的解:
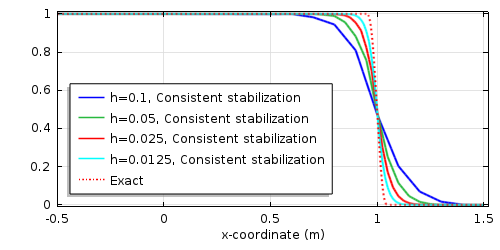
自洽稳定方法保证了问题在空间上得到很好的解决。因为我们正在求解一个瞬态问题,所以查看瞬态求解器设置以确保问题也能及时得到很好的解决也是一个好主意。在 COMSOL Multiphysics 中,瞬态求解器的精度由相对和绝对误差容限控制。
下图显示了用户定义的误差容限函数的解:
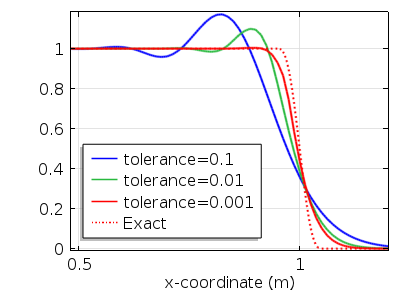
当误差容差太松时会观察到数值过冲会以及这个数值过冲会在容差等于 1e-3 时消失,会观察到。更严格的容差会导致更准确的结果,但会增加计算负载。默认情况下,相对和绝对误差容限分别设置为 1e -2和 1e -3。
物理场-细节技巧
1.稀物质和浓物质传递
稀物质传递 接口提供了额外的高级选项。一种选择是残差的内部计算。为了节省时间,通常不需要计算当前解的完整残差,而是通过忽略扩散张量分量的导数来近似计算。

此外,您可以在两种不同的侧风扩散方法之间进行选择:“Do Carmo and Galeão”(默认)和 “Codina” 公式。第一个将过冲和下冲降至最低,也适用于各向异性网格。当问题收敛时,即使对于最佳网格,您也应该切换到第二个公式。与 “Do Carmo and Galeão” 选项相比,“Codina” 公式的扩散较小,但会导致更多的下冲和上冲。
与 “Do Carmo and Galeão” 选项相比,“Codina” 公式的扩散性更小,但可能导致更多的不足和过冲。

2.流体流动
一般情况下,不应在流体流动接口中修改稳定性设置。在使用独立于 Péclet 数的默认 P1 + P1 单元时,Navier-Stokes 方程不稳定,并且始终需要自洽稳定性(有关详细信息,请参阅 I. Babuška 和 F. Brezzi 的工作)。Pm + Pn 表示速度用 m 阶计算单元解析,而压力用 n 阶元素解析。
只有当速度以高于压力(P2 + P1 和 P3 + P2)的更高阶解析且 Péclet 数较小时,才能移除默认的自洽稳定性。这些计算单元(P2 + P1 和 P3 + P2)应该只在流动被网格很好地解析时使用。在这种情况下,稳定项对解的影响无论如何都可以忽略不计,删除它不会影响我们的结果。
3.基于方程建模
COMSOL 软件中的物理场接口包括稳定方法。但是,如果我们使用自己的传递方程,那么就需要对特定应用的稳定方法进行一些文献综述,并自己实现稳定方程。第一次尝试可以包括手动向扩散参数添加人工扩散。如何手动实现稳定项示例讲解了如何操作。
结论与替代方法
你不需要更改默认稳定设置! COMSOL 开发人员在添加一致的人工扩散方面做得非常出色,因此不必担心稳定性问题。当网格太粗糙时,自洽性稳定性会有所帮助,当网格很好地解析方程时则会隐藏起来。但是请注意,还有另一种不需要任何人工或黏性扩散就可解决质量传递问题的方法。
是的,与基于网格的方法(即,有限元、有限差分、有限体积)不同,基于拉格朗日粒子的方法 可以非常有效地模拟高 Péclet 数问题,而无需添加人工扩散。粒子追踪模块中提供了这种替代方法。COMSOL 认证顾问 Veryst Engineering 与 Nordson EFD 合作开发了层流静态混合器的计算模型,并找到了改进和优化其性能的方法。使用 COMSOL Multiphysics 和粒子追踪模块,他们能够从模拟中排除数值扩散以获得更准确的解决方案,使用的计算资源比使用基于网格的方法少得多。
为了让你开始使用 COMSOL Multiphysics,COMSOL 案例库包含了一个用这两种方法解决静态混合器的例子,(层流静态混合器和层流静态混合器中的颗粒轨迹)。同样,关于数值稳定的更多细节和参考文献可以在 COMSOL 多物理参考手册中找到。






评论 (1)
峰 杜
2024-08-08在接触对设置中的稳定性的作用是什么?