Menu
COMSOL 博客

什么是旋度单元，为什么要使用它？

Author Image
作者 Lipeng Liu
2019年 12月 30日

旋度单元，有时也称为边单元或矢量单元，广泛用于有限元法中以解决电磁学问题。今天这篇博文全面介绍了这种类型的单元，包括为什么是旋度单元以及如何在 COMSOL Multiphysics® 软件中使用它。然而，理解为什么以及如何使用旋度单元并不简单。因此，我们将会先复习一些关于麦克斯韦方程组和有限元法的背景知识。

电磁学中要求解的 2 种基本方程形式

电磁学建模的目标是求解受特定边界条件约束的麦克斯韦方程组。麦克斯韦方程的微分形式如下：

(1)

\nabla \cdot \textbf{D} = \rho

 

(2)

\nabla \times \textbf{E}=-\frac {\partial \textbf{B}}{\partial t}

 

(3)

\nabla \cdot \textbf{B} = 0

 

(4)

\nabla \times \textbf{H} = \textbf{J} + \frac {\partial \textbf{D}}{\partial t}

 
其中 \textbf{E} 和 \textbf{H} 分别是电场强度和磁场强度；\textbf{D} 和 \textbf{B} 分别是电位移场和磁通密度；{\rho} 和 \textbf{J} 分别是电荷密度和导电电流密度。

为了获得一个封闭系统，麦克斯韦方程包括描述介质宏观属性的本构关系。借助 COMSOL Multiphysics，您可以对各种不同的介质进行建模，包括非线性和各向异性材料。然而，为了简单起见，我们忽略了剩磁效应并假设介质是线性和各向同性的，从而得到一个简单的本构关系，如下所示：

(5)

\textbf{D} = \epsilon \textbf{E}
\textbf{B}= \mu \textbf{H}

其中 \epsilon 是介电常数，\mu 是磁导率。

请注意，方程 (1) – (4) 对连续介质中的点有效，而在介质 1 和 2 之间的不连续界面处，边界条件表示为：

(6)

\textbf{n}_2 \cdot (\textbf{D}_1 – \textbf{D}_2) = \rho_s

 

(7)

\textbf{n}_2 \times (\textbf{E}_1 – \textbf{E}_2) = \textbf{0}

 

(8)

\textbf{n}_2 \cdot (\textbf{B}_1 – \textbf{B}_2) = 0

 

(9)

\textbf{n}_2 \times (\textbf{H}_1 – \textbf{H}_2) = \textbf{J}_s

 
其中 \bf{n_2} 是介质 2 的向外法向， {\rho_s} 和 \textbf{J}_s是表面电荷密度和表面电流密度。

方程(7)和方程(8)代表切向电场和磁通密度场的法向分量在边界处是连续的，而方程(6) 和方程(9) 意味着电通量场的法向分量和切向磁场可以是不连续的。

对于特定问题，求解麦克斯韦方程组的子集或特殊情况总是很方便的，从而产生不同的电、磁或电磁公式。基于这些公式，COMSOL Multiphysics 软件包含了多个电磁模块（例如，AC/DC 模块、RF 模块和波动光学模块），以及每个模块中的多个不同物理场接口。

例如，AC/DC 模块中的静电 接口可以模拟仅存在静电荷的静电问题。对于这类问题，我们只需要求解方程(1)和方程(2)。通过引入电势 V 并定义 \textbf{E}=-\nabla V,方程(1)和方程(2)被简化为一个方程，即泊松方程，因为 \nabla \times \nabla \textit{V} = 0 始终成立。泊松方程表示为：

(10)

\nabla \cdot (\epsilon \nabla \textit{V} )= – \rho

在 COMSOL Multiphysics 中，所有的标量电势接口都用一个形式的泊松方程表示。对于没有电流的磁场，方程(4)被简化为类似于静电场的形式。通过引入磁标量势，这个问题也可以表述为泊松方程。对于其他情况，我们必须求解矢量公式。例如，对于仅存在静态电流的静磁场，我们只需要求解方程(3)和方程(4)。通过引入磁矢量势 \textbf{A} 并定义\textbf{B}=\nabla \times \textbf{A}等式(3) 和等式(4) 被简化为下面的方程，因为 \nabla \cdot (\nabla \times \textbf{A} )= 0 始终成立。

(11)

\nabla \times (\frac {1}{\mu} \nabla \times \textbf{A} )= \bf{J}

方程(11)用包含 \nabla \times (\nabla \times .) 算子的矢量方程的形式表述，其他的情况，比如电磁波也是用这种形式表述的。

为便于讨论，我们以时谐场为例。在频域中，将方程(2)代入方程(4)得到

(12)

\nabla \times (\frac {1}{\mu} \nabla \times \textbf{E} ) – \omega^2 \epsilon \textbf{E}= – j \omega \textbf{J}

其中，\omega是频率，j 是虚数单位。

形函数和拉格朗日单元

在 COMSOL Multiphysics 中，有限元法(FEM)通常用于求解偏微分方程(PDE)，麦克斯韦方程组也不例外。有限元法分几个步骤求解偏微分方程，包括：

  1. 将域划分为许多小的、不重叠的单元，这些单元素称为网格单元。
  2. 每个单元中的解由局部形函数或基函数近似表示。
  3. 将偏微分方程写成弱形式，对每个网格单元进行离散化以获得局部矩阵
  4. 将局部矩阵组装成全局矩阵，然后求解。

我们以泊松方程(10)为例来说明有限元法是如何工作的。我们可以根据使用的形函数使用不同的单元。为简单起见，我们认为域是二维的，并使用线性三角形拉格朗日单元。顶点 i,j,k 单元中的电势 V 可以用线性函数 N_{i,j,k}(x,y) 近似表示为

(13)

V(x,y) =
\begin{bmatrix}
V_i, V_j, V_k
\end{bmatrix}
\begin{bmatrix}
N_i(x,y) \\
N_j(x,y) \\
N_k(x,y)
\end{bmatrix}
= V_i N_i(x,y)+V_j N_j(x,y) + V_k N_k(x,y)

从中我们可以看到，每个顶点都增加了一个自由度（DOF），相应的形函数在顶点处等于 1，而在所有其他顶点处为 0。高阶拉格朗日单元不仅在顶点上位于单元上，而且在其他节点也位于单元上。因此拉格朗日单元也称为节点单元。线性三角形拉格朗日单元的形函数如下图所示。

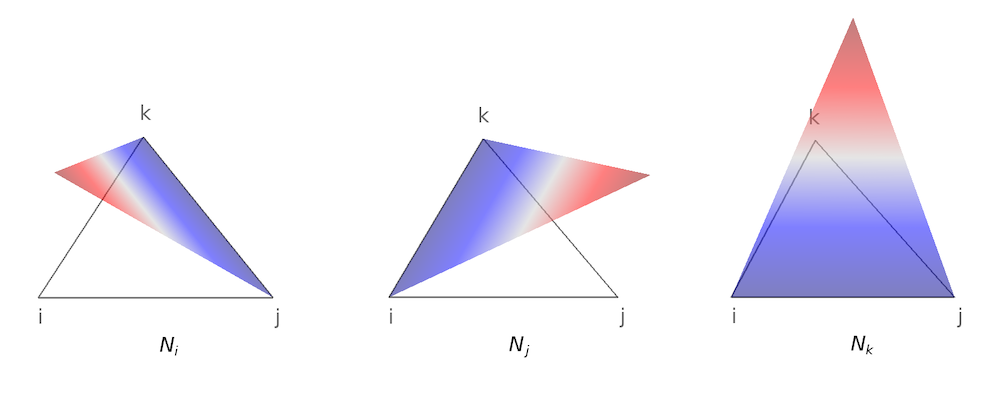
线性三角形拉格朗日单元的形状函数图。

拉格朗日单元不仅在每个单元中连续，而且在边界上连续，如下图所示。

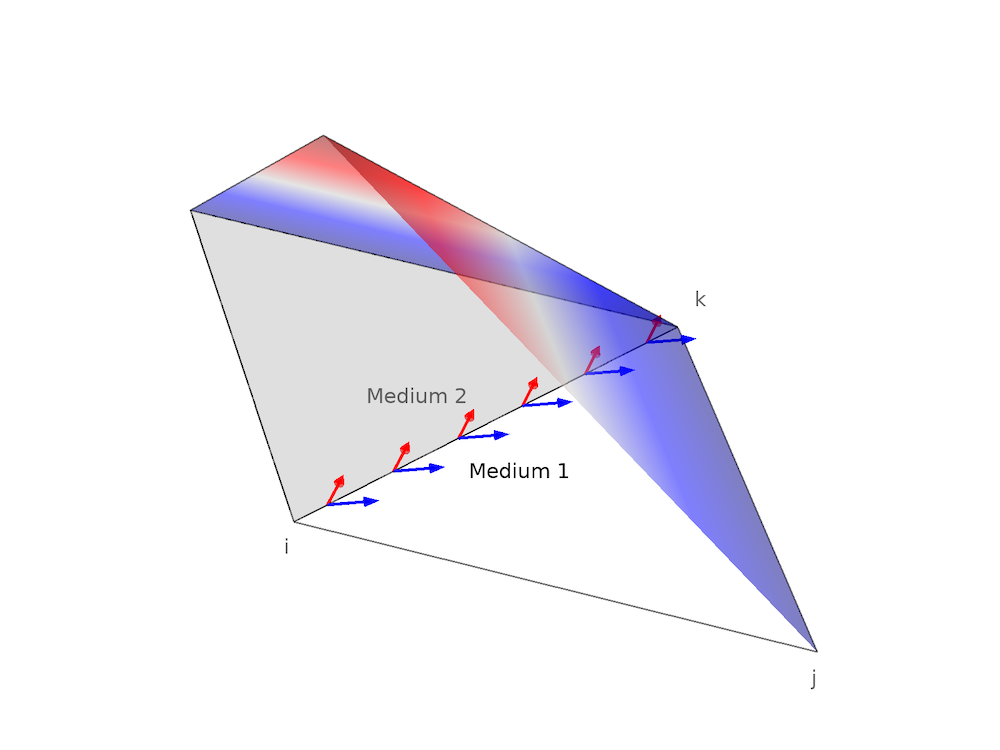
拉格朗日元素跨边界连续的图形。

介质 1 和介质 2 共享同一个边界 ki。靠近边界 ki 的电场分别在介质 1 和 2 中以蓝色和红色箭头绘制。由于电势 V 在边界上是连续的，因此 V 的切向梯度（即切向电场）是连续的。换句话说，边界条件方程(7)自动满足。因此，我们只需要考虑方程(6)中存在表面电荷的地方。接下来，我们将展示 FEM 如何自然地处理这个问题。

推导泊松方程(10)的弱形式并不困难。将测试函数乘以 \phi等式(10)的两侧，域上的积分给出

(14)

\int_{\Omega} \nabla \cdot (\epsilon \nabla \textit{V} )\phi= \int_{\Omega} – \rho \phi

 

对方程左侧进行部分积分得到

(15)

-\int_{\Omega} \epsilon \nabla \textit{V} \cdot \nabla \phi + \int_{\partial \Omega} \epsilon \nabla \textit{V} \cdot \textbf{n} \phi= \int_{\Omega} – \rho \phi

\partial \Omega 是域的边界，\textbf{n} 是远离域的法向量。

这一步很重要并且有 2 个优势：

  1. 减少空间导数的最大阶，这使得用线性（一阶）单元求解二阶偏微分方程成为可能；
  2. 明确方程的自然边界条件（如果不考虑则自动满足）是什么。

如果 \nabla \textit{V}  的法线分量在边界上消失，则左侧的第二个积分消失。为了清楚地了解它是如何工作的，将等式(15)重写为

(16)

\int_{\Omega} \textbf{D} \cdot \nabla \phi – \int_{\partial \Omega} \textbf{D} \cdot \textbf{n} \phi= \int_{\Omega} – \rho \phi

很明确，自然边界条件为 \textbf{D} \cdot \textbf{n}=0。

在 AC/DC 模块的静电接口中，该自然边界 条件被设置为默认值。对于边界条件不是由电势而是由电荷密度给出的情况，可以直接将边界条件方程(6)合并为等式(16)。

旋度单元

也可以使用基于拉格朗日单元的有限元法将矢量方程(12)分解为不同的分量来求解 \textbf{E}_{x,y,z}。然而，描述边界条件很复杂，特别是对于不规则边界。即便如此，结果可能是虚假的，因为拉格朗日单元会强制使每个分量 \textbf{E}_{x,y,z} 在边界上是连续的，这违反了电场的法向分量在材料界面处可能不连续的事实，尤其是在锐角边界处。

我们以 COMSOL 案例库中的 Sierpinski 分形单极天线模型为例。分形辐射器在 1.6 GHz 的表面电场如下图所示。很明显，边缘 \textbf{E}_{x,y,z} 发生了很大变化。

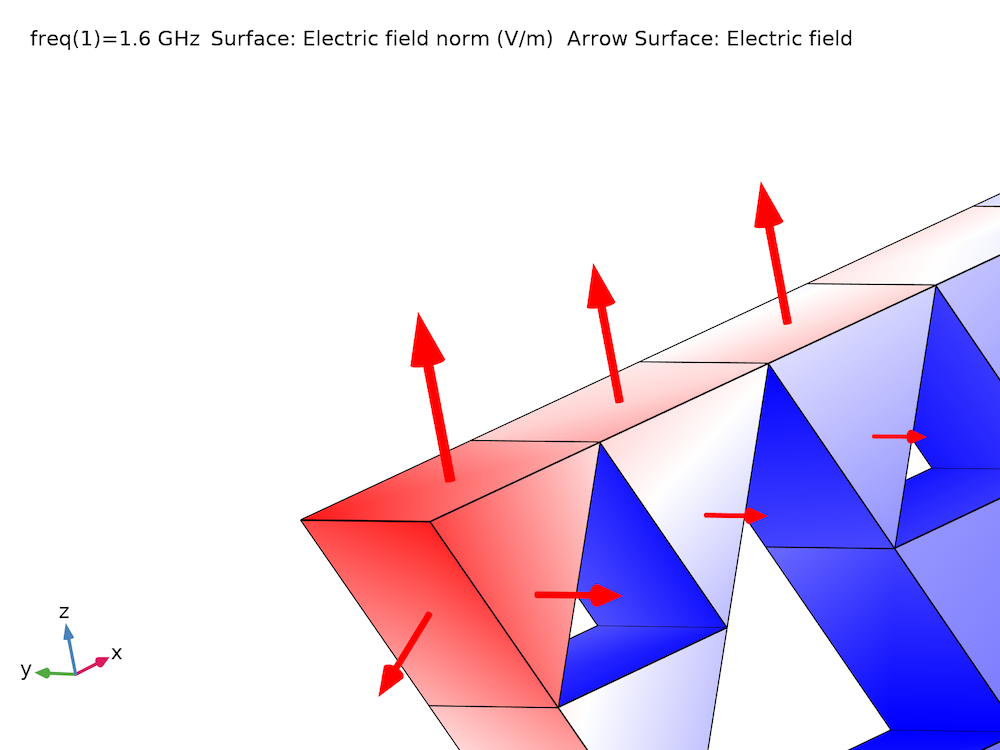
COMSOL Multiphysics中 Lagrange 元素的图形，使用标量形状函数来近似标量场。

如前所述，拉格朗日单元使用标量形函数来近似标量场。使用矢量形函数来近似矢量场是很自然的。例如，方程(12)中的电场可以表示为：

(17)

\textbf{E} = E_i \textbf{W}_i+E_j \textbf{W}_j + E_k \textbf{W}_k

如方程(17)所示，不适合在节点上添加自由度，因为矢量场也有方向。为了获得一个标量值，我们可以在每条边上添加自由度，因为沿边的矢量场分量（切向分量）是一个标量。然后，我们将等式(17)改写为：

(18)

\textbf{E} = E_{ij} \textbf{W}_{ij}+E_{jk} \textbf{W}_{jk} + E_{ki} \textbf{W}_{ki}

与拉格朗日形函数类似，矢量形函数沿一条边的切向分量是非零常数，而沿其他边则为零。满足上述性质的一种形函数是 Whitney 1 型基函数(参考文献 1，参考文献 2)，其表示为：

(19)

\textbf{W}_{ij} = N_i \nabla N_j – N_j \nabla N_i
\textbf{W}_{jk} = N_j \nabla N_k – N_k \nabla N_j
\textbf{W}_{ki} = N_k \nabla N_i – N_i \nabla N_k

一阶三角形边单元的形函数如下图所示。

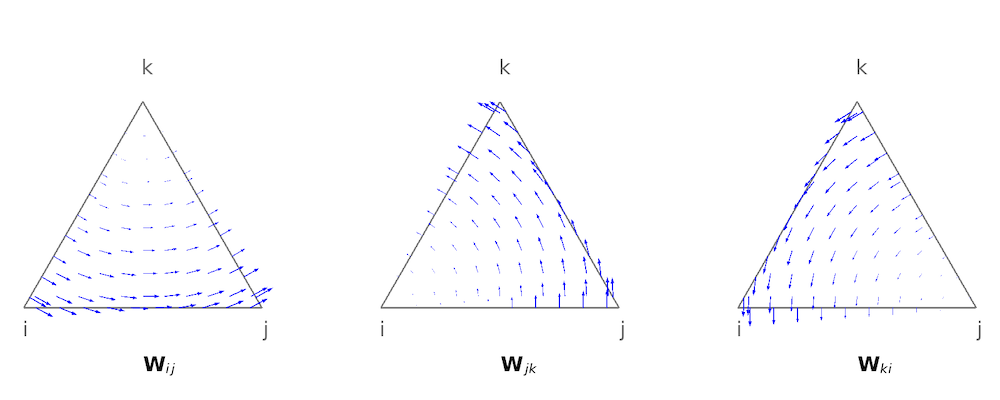
一阶三角形边元素的形状函数图。

从数学的角度来看，边单元在 H(curl) 空间中是一致的(参考文献3)，因此它也被称为旋度单元。在 COMSOL Multiphysics 中，我们使用更通用的名称“旋度单元”，因为高阶单元不仅在边上添加了更多自由度，还在单元内部添加了更多自由度。类似于我们为两个相邻的拉格朗日单元绘制的图，共享同一边界 ki 的两个旋度单元的基函数如下所示

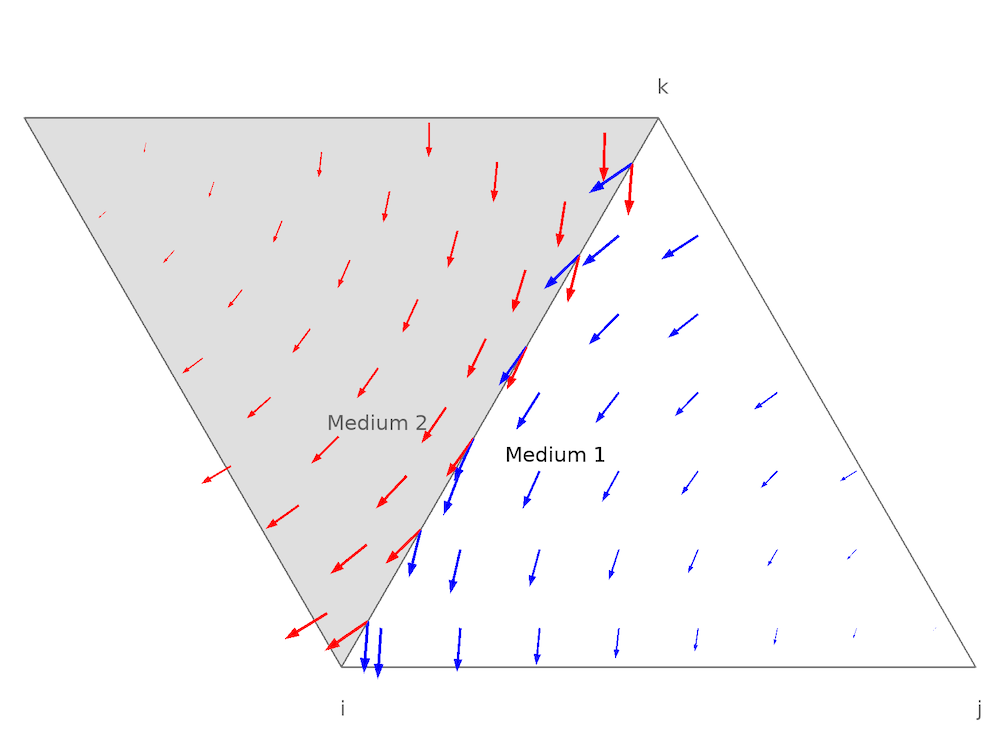
共享同一边界的两个旋度元素的函数图。

我们可以看到跨边界的切向电场是连续的，这与使用拉格朗日单元求解泊松方程的情况非常相似。因此，通过使用旋度单元，边界条件方程(7)自动满足。接下来，让我们来看看如何使用有限元法求解边界方程(9)。

与求解泊松方程 \textbf{W} 类似，将测试函数乘以等式(12)的两边，域上的积分为 \Omega

(20)

\int_{ \Omega} \nabla \times (\frac {1}{\mu} \nabla \times \textbf{E} ) \textbf{W}=\int_{ \Omega} (\omega^2 \epsilon \textbf{E} – j \omega \textbf{J}) \textbf{W}

对左侧进行部分积分得到

(21)

\int_{ \Omega} (\frac {1}{\mu} \nabla \times \textbf{E} ) (\nabla \times \textbf{W}) + \int_{\partial \Omega} \textbf{n} \times (\frac {1}{\mu} \nabla \times \textbf{E} )\textbf{W} =\int_{ \Omega} (\omega^2 \epsilon \textbf{E} – j \omega \textbf{J}) \textbf{W}

重写等式左边的第二部分，可以得到

(22)

\int_{ \Omega} (\frac {1}{\mu} \nabla \times \textbf{E} ) (\nabla \times \textbf{W}) -j \omega \int_{\partial \Omega} ( \textbf{n} \times \textbf{H} )\textbf{W} =\int_{ \Omega} (\omega^2 \epsilon \textbf{E} – j \omega \textbf{J}) \textbf{W}

我们可以看到，边界条件方程(9)可以很容易地并入弱表达式。

旋度单元的优缺点

我们已经证明，通过使用旋度，可以自然地处理麦克斯韦方程的边界条件。旋度单元强制切向电场是连续的，并允许法向电场跨越边。此外，它还可以更容易地约束其他边界条件（参考文献4）。

例如，在电磁波，频域接口中，完美电导体边界特征被设置为默认值，用于模拟导电表面，例如金属。边界条件强制切向电场为零 \textbf{n} \times \textbf{E} = \textbf{0}，即在磁场接口中，默认边界条件是磁绝缘，它将切向磁矢量势约束为零，即 \textbf{n}\times \textbf{A}= \textbf {0} 使用逐点约束的有限元法可以很容易地考虑这些边界条件，因为未知数正是边界上的切向场。使用旋度单元还有其他优点，例如消除杂散解，尤其是解决电磁波问题（参考文献5）。然而，边界条件的自然处理应该占主导地位。

使用旋度单元也有一些缺点。例如，线性旋度单元的局部近似误差为 O(h)，其中 h 是单元大小，而使用线性拉格朗日单元时，局部误差收敛于 O(h^2)（参考文献6）。这是因为旋度单元是一个混合单元，其中形函数的阶次在不同方向上变化。例如，形函数 \textbf{W}_{ij} 沿边 ij 和任何平行于边 ij 方向的切向分量都是常数，尽管它在其他方向上是线性函数。也可以通过查看分量来显示混合属性，例如，

(23)

\textbf{W}_{ij} = N_i \nabla N_j – N_j \nabla N_i
=(a_i+b_i x+c_i y)(b_j, c_j)-(a_j+b_j x+c_j y)(b_i,c_i)
=(d_i + d_{ij} y, d_j – d_{ij} x)

a,b,c,d 是常数，仅取决于元素的坐标。

\textbf{W}_{ij} 的 x 分量是沿 x 轴的常数，沿 y 轴是线性的。每个分量的空间导数的精度有显著差异。因此，在对旋度单元进行后处理时，场的高阶空间导数不可用。方程(23)还表明线性旋度单元的形函数可以沿特定方向保持不变。这使得局部误差收敛比使用线性拉格朗日元素慢。一方面，这个缺点可以通过使用高阶旋度单元或更细的网格来消除。另一方面，与自然处理边界条件的优点相比，此缺点变得不那么重要，因为使用拉格朗日单元求解方程(12)遇到的困难不能通过使用高阶形函数或细化网格来弥补。

结束语

在这篇博文中，我们先从麦克斯韦方程及其边界条件开始，介绍了电磁建模中经常出现的两种基本类型的方程；即标量泊松方程和带算子的向量方程 \nabla \times (\nabla \times)。我们已经证明，利用经典拉格朗日单元求解泊松方程，自然地满足连续切向电场的条件。然而，由于难以处理相关的边界条件，不适合使用拉格朗日单元来求解矢量方程。

然后我们引入了旋度单元，可以自然地满足连续切向电场的条件。同时，我们还通过详细推导弱表达式，展示了如何为其他边界条件引入有限元法。最后，我们谈到了使用旋度单元的一些缺点，但是这些缺点远没有优点重要。

参考文献

  1. Whitney, Geometric integration theory, Princeton UP, Princeton, 1957.
  2. Nentchev, Numerical analysis and simulation in microelectronics by vector finite elements, 2008.
  3. C. Nédélec, Mixed finite elements in ℝ3 . Numerische Mathematik,35(3), pp. 315–341, 1980.
  4. P. Webb, Edge elements and what they can do for you. IEEE Transactions on Magnetics, 29(2), pp.1460–1465, 1993.
  5. M. Jin, Theory and computation of electromagnetic fields. John Wiley & Sons, 2011.
  6. Mur, Edge elements, their advantages and their disadvantages. IEEE transactions on magnetics, 30(5), pp.3552–3557, 1994.

博客分类

相关主题

评论 (0)

正在加载...
浏览 COMSOL 博客
类别
标记