在 COMSOL® 中对移动载荷和约束进行建模的 3 种方法

COMSOL Multiphysics^® 软件的核心优势之一是能够轻松定义随时间变化的载荷和约束。有几种不同的方法可以做到这一点，这些都属于软件的核心功能。在今天的博客中，我们将给大家介绍其中的三种方法，并用实际案例演示如何使用这些方法。

示例：平板的激光加热

假设有一个被激光热源加热的平板材料，如下图所示。这个平板以原点为中心，我们希望随着时间的变化，在不同的位置加热它的表面。假设激光器（或工件）安装在一个能对焦点进行定位控制的平台上。同时假设有一些光学器件可以形成具有一定轮廓的激光束，因此热源分布在焦点周围的一个小区域内。

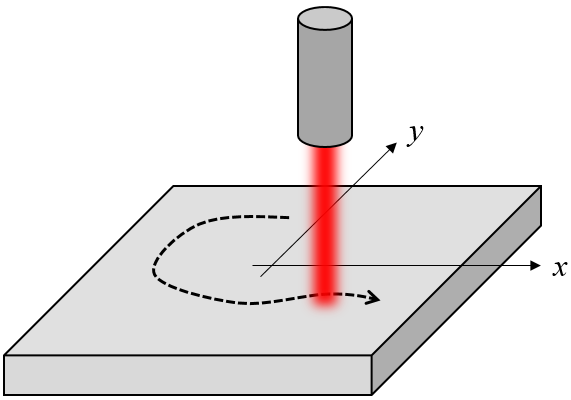
激光热源穿过一个工件的示意图。

现在，让我们看看几种不同的方法，通过这些方法可以定义移动焦点，使其遵循已知的工具路径。

方法1：使用变量

最简单的方法是使用一组变量来定义焦点的位置和热载荷随时间的分布。假设我们想让一个 1kW 的总热载荷每 10s 在半径为 40cm 的圆形路径上移动一次。此外，热载荷有一个高斯强度分布，腰束半径为 5cm。我们可以使用变量来定义这些信息，如下面的屏幕截图所示。

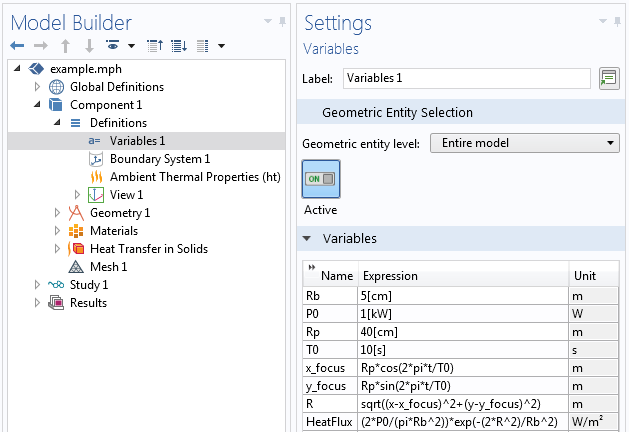
前四个定义，Rb、P0、Rp 和 T0，实际上只是常量。如果我们稍后想通过参数化扫描来更改这些定义中的任何一个，也可以把它们定义为 全局参数。目前，最简单的方法是将它们全部显示在一个地方。

接下来的两个变量 x_focus 和 y_focus 不是常数：它们是时间的函数，随时间的变化而变化，即内置变量 t。我们可以看到这些变量描述了一个围绕原点做圆周运动的点，即：

Rp*cos(2*pi*t/T0)

Rp*sin(2*pi*t/T0)

下一个变量 R 是一个时间和空间的函数。它利用了坐标变量 x 和 y，以及 x_focus 和 y_focus，它们是时间的函数。因此，在每个时间点和空间中的每个点上，这个变量表示到激光焦点的距离（在 xy 平面上）。

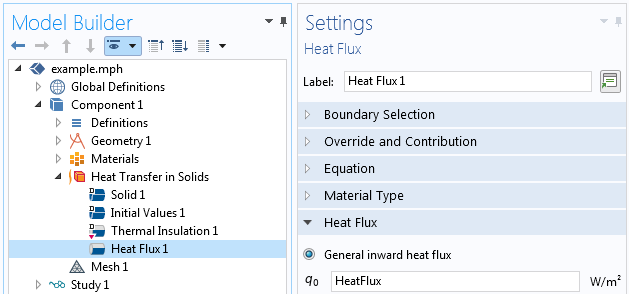
最后一个变量 HeatFlux 是变量 R 和常数 Rb、P0、Rp 和 T0的函数。它定义了围绕焦点的高斯强度曲线，以使总热通量等于定义的功率。我们将这个变量 HeatFlux 作为边界条件输入，如下面的屏幕截图所示。

根据规定的热通量表达式，可以得到下图所示的加热曲线路径。

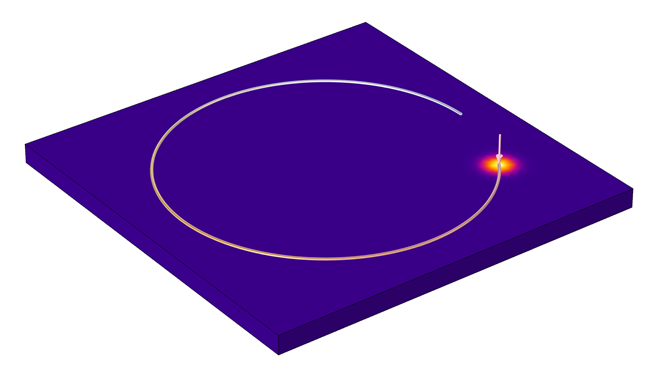
通过 变量节点设置的循环加热曲线。

方法2：使用插值函数

上面讲的方法只是使用了一些并不复杂的表达式，我们还可以用更通用的方式来代替 x_focus 和 y_focus 的简单表达式。COMSOL Multiphysics 软件中提供了各种内置函数。对于我们这里讨论的内容，最有用的是插值 函数，它可以让我们从文本文件中读入数据。假设我们有一个文本文件，其中包含时间行数据以及当时激光焦点的 x 和 y 位置。下面就是一个文件示例。

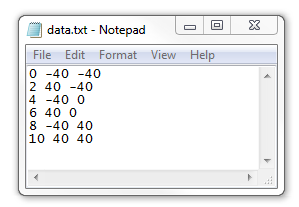
我们可以使用如下所示的设置将这类数据读入插值函数。请注意，这里只有一个参数，即时间，之后的两列数据分别表示焦点的 x 坐标和 y 坐标，单位为厘米。在指定的时间点之间，我们希望激光线性地移动。将函数名称分别指定为 x_f 和 y_f，并确保正确设置参数。

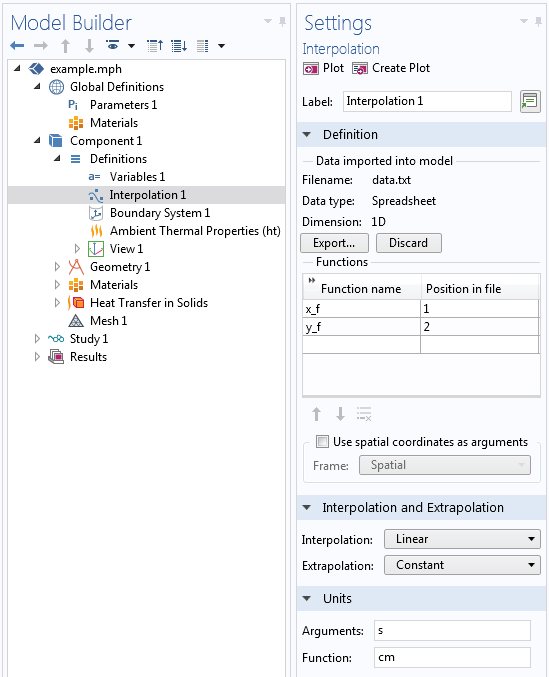
然后，我们可以改变之前的焦点表达式 x_focus = x_f(t)， y_focus = y_f(t)，并得到下图所示的移动载荷。

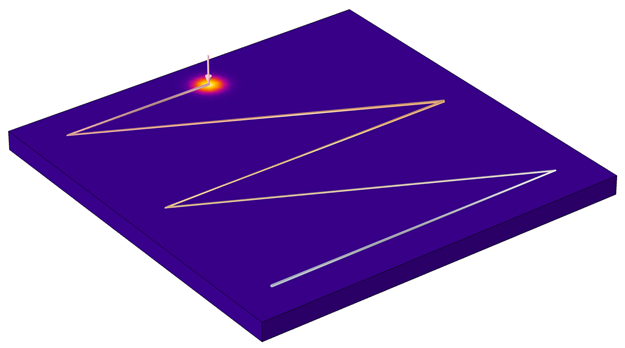
从文本文件中读取数据的加热曲线。

可以看到，这个插值函数可以让我们快速读取一些非常复杂的轮廓，我们只需要一种生成这些轮廓和文本文件的方法。例如，这里使用的文本文件格式与 G 代码格式没有太大区别，所以如果我们有一个用这种格式定义的加热路径，就可以非常简单地将它转换为对 COMSOL^® 友好的输入。另外，也许我们还想导入一个常用的二维DXF格式的轮廓。接下来，让我们接下来看看这个问题怎么实现。

方法3：使用从 CAD 几何图形导入的路径

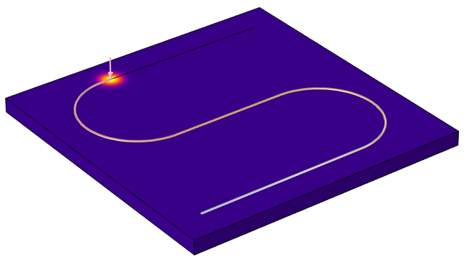
假设我们希望载荷沿着从外部文件中读取的路径移动，如下图所示，我们希望激光沿着这条路径从一端平滑地移动到另一端。

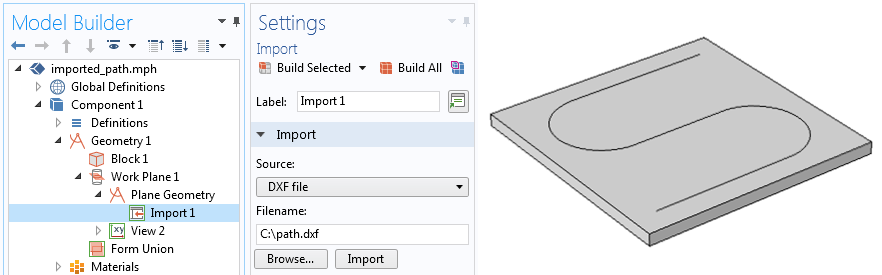
激光路径的S形轮廓是作为一个几何图形从 DXF 文件中读入的。

我们读入的文件中没有任何关于时间的信息：这只是我们期望激光以恒定速度遵循的路径。现在，这条导入路径的每条边（可能有数千条边）确实有参数 s1 和 s2，这些参数沿长度线性变化，但是如果有很多边，我们可能不想使用这些参数。那么，该如何计算激光在整个线组的每个时间点上的位置呢？我们可以通过引入一个偏微分方程（PDE）沿着所需的线组来解决这个问题。我们要求解的 PDE 是：

其中,\nabla_t 指曲线的切线方向。

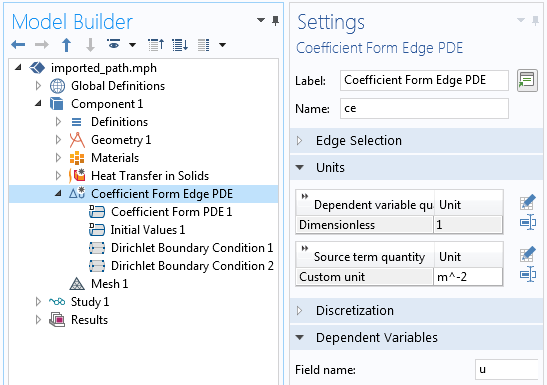
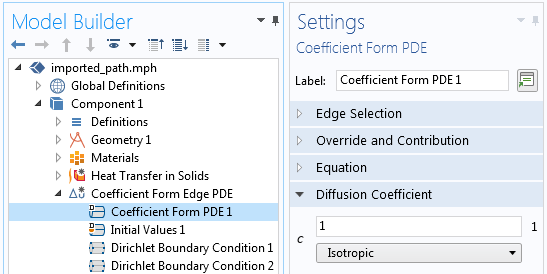
通过在路径两端分别设置 u=0 和 u=1 的边界条件，这个 PDE 将给出一个沿路径从0到1线性变化的场，对应路径所有边总弧长的比例。在 COMSOL 软件中，我们可以使用 系数形式边偏微分方程 接口来设置，如下面的屏幕截图所示。除了扩散系数 c 以外的所有系数项都设置为零。

左：计算路径所需的 系数形式边偏微分方程 接口的设置。右：扩散系数项 c 是一个常数；所有其他系数都设置为零。

首先使用两个狄利克雷 边界条件对场 u 的两端进行设置，然后在同一研究中，先以稳态步骤求解该偏微分方程，再求解传热问题。

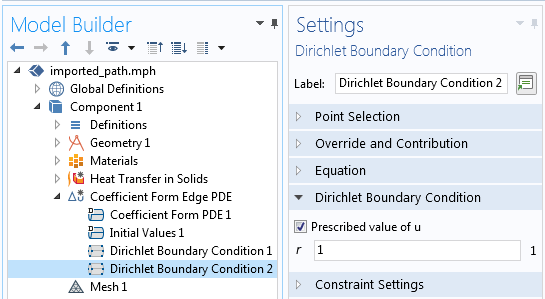
在路径的起点和终点使用两个 狄利克雷边界条件来约束场。

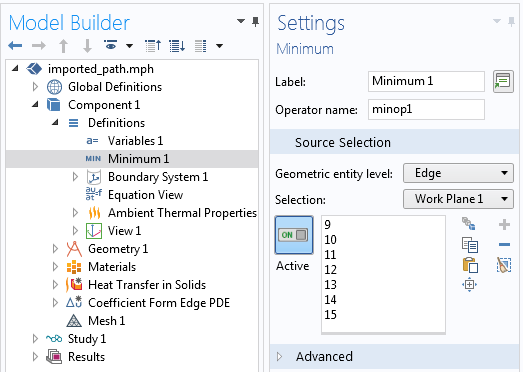
接下来，我们在模型中引入一个最小值耦合算子，将路径的边作为算子的源。这个最小值算子被用来定义焦点坐标，例如：

x_focus = minop1(abs(u-t/T0),x)

y_focus = minop1(abs(u-t/T0),y)

请注意，最小值算子被赋予两个参数。当我们调用带两个参数的算子时，它将返回第一个参数处于最小值时第二个参数的值。因此，在每个时间 t，它将返回边上的一个点位置的 x 和 y 坐标，该点为路径两端 t/T0 分数处的点。

左图：在热源所遵循的路径上定义了最小值算子。右图：沿着导入的 DXF 文件定义的激光热源路径。

如果我们想让激光以不同的速度穿过路径的不同部分，该怎么办呢？我们只需要沿着这些边界调整系数 c 就可以了。假设我们想让激光沿着弯曲的边界移动比沿着直线移动快三倍，只需将 c 放大三倍就可以了。请注意，绝对值并不重要，重要的是系数数值的比率。当路径存在交叉时，就会出现该方法的一个缺点。在这种情况下，我们需要将路径细分为两组或更多的路径；对每组路径进行 PDE 求解；并对变量做更多的统计工作。

结束语

在这篇博文中，我们研究了三种不同的对移动载荷进行建模的方法。如果您想亲自动手尝试模拟这些案例，请单击下面的按钮前往 COMSOL 案例库。在那里，您可以下载上述模型的 MPH 文件。

案例库中的其他几个示例也使用了文中介绍的这些技术，包括：

• 硅晶片的激光加热
• 承受动载荷的梁

尽管在这篇博文中我们只考虑了载荷，但是请注意，我们也可以将这些技术应用于约束，例如，如何在您的模型中设置边界条件。

您对使用 COMSOL Multiphysics 进行建模的应用还有其他疑问吗？请告诉我们！