含热粘性损耗的声学拓扑优化

今天，来自丹麦 GN Hearing 公司的特邀博主 René Christensen 与我们一起讨论如何在微型声学设备的拓扑优化中加入热粘性损耗。

拓扑优化有助于工程中在特定先验 目标的指导下，以更优的方式进行应用设计，拓扑优化主要应用于结构力学，在热学、电磁学和声学领域亦有所应用。直到去年，微观声学才出现在这个名单中。本篇博客文章介绍了一种包含热粘性损耗的微观声学拓扑优化新方法。

标准声学拓扑优化

之前一篇关于声学拓扑优化的博客文章概述了相关的基础理论，并列举了数个案例。声学描述采用亥姆霍兹波动方程。借此方程，我们可以对各种不同应用进行拓扑优化，比如扬声器箱体、波导、室内装饰、反射器布置和类似的大型几何结构。

控制方程是标准的波动方程，材料参数通过密度 \rho 和体积模量 K 来指定。在拓扑优化中，密度和体积模量通过变量 \epsilon进行插值。理想情况下，此插值变量采用二进制值：0 代表空气，1 代表固体。不过，在优化过程中，它的值遵循插值公式，例如图 1 的固体各向同性材料罚函数（solid isotropic material with penalization，简称 SIMP）模型。

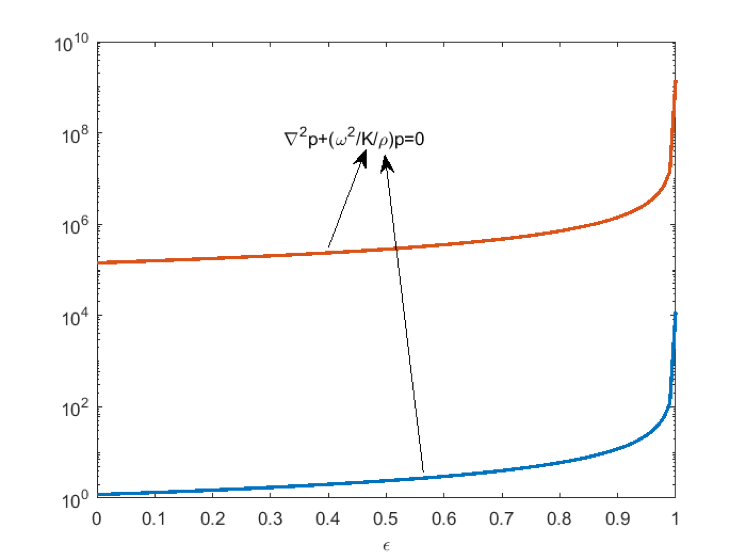
图 1：标准声学拓扑优化的密度和体积模量插值。为了在同一张绘图中显示两个值，我们省略了单位。

该方法适用于那些可以忽略的热粘性损耗（靠近壁面的声学边界层中）的应用。优化域可耦合到狭窄区域中，例如利用均质模型来描述的狭窄区域（这是压力声学、频域 接口中的狭窄区域声学 特征）。不过，如果发生热粘性损耗的狭窄区域自身的形状产生了变化，此优化算法便不再有效，波导横截面变形便属于此类情况。

热粘性声学（微观声学）

对于诸如助听器、移动电话、特定超材料几何结构等微观声学应用，声学方程一般需要显式添加热粘性损耗，这是因为主要损耗发生在靠近壁的声学边界层中。下方图 2 展示了上述效应。

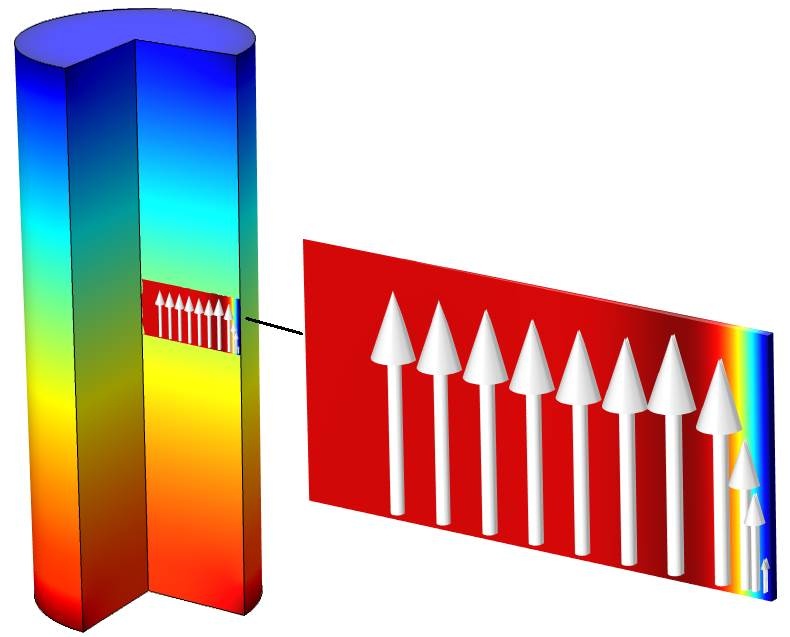
图 2. 体内场是声压，表面场是温度变化，箭头表示速度。

声波从圆形截面管道的底部向顶部传播。压力显示在 ¾ 旋转绘图中。

箭头表示此特定频率下的粒子速度。靠近边界的粒子速度很慢，在边界上趋近于零。然而在腔体内，粒子按照欧拉方程以标准的声学速度运动。在粘性作用下，空气被“粘”到边界上，因此边界速度为零。邻近的粒子也慢了下来，导致了总体能量损耗，或者说声能转换成了热能（由于剪切产生的粘性耗散）。但是在腔体内，分子可以自由地运动。

热粘性声学控制方程

对微观声学（包含与声学边界层的相关损耗）进行详细建模，这要求在静态条件下求解一组线性纳维-斯托克斯方程。COMSOL Multiphysics® 软件的“声学模块”中的热粘性声学 物理场接口能实现这些方程。不过，若拓扑优化需要应用某些假设条件，该方程式则不适用。参考文献 1 提出了基于亥姆霍兹分解的公式。该公式对于很多微观声学应用均有效，并且能够对热波、粘性波和压缩（压力）波解耦。一个近似但准确的表达式（参考文献 1）描述了速度和压力梯度的关系：

其中，粘性场 \Psi_{v}是一个标量的无量纲场，它描述了域内条件与边界条件之间的差异。

上方的彩色表面图显示了声学温度的变化。边界上变化为零，是因为固体壁的导热系数很高，但是腔内的温度变化可以利用等熵能量方程进行计算。温度变化和声学压力的关系可以写作一般形式（参考文献 1）：

其中，热场 \Psi_{h} 是一个标量的无量纲场，它描述了域内条件与边界条件之间的差异。

我们会在下文中解释，为何粘性场和热场对于创建拓扑优化算法必不可少。

热粘性声学应用的拓扑优化

与标准的声学拓扑优化相反，热粘性声学没有既定的插值公式。由于没有准确描述热粘性物理现象的单方程系统（它通常需要三个控制方程），所以没有明显可插值的变量。本节将为您介绍一个新颖的算法。

为了简单起见，我们只讨论横截面不变的波导内的波传播。这等效于称为“Low Reduced Frequency”的模型，微观声学从业者可能对它比较了解。粘性场可以通过方程 1 来计算（参考文献1）：

(1)

其中， \Delta_{cd}仅为横截面方向的拉普拉斯算子。对于某些简单的几何结构，我们可以对场进行解析计算（例如压力声学，频域 接口中的狭窄区域声学 特征中的操作）。不过，当用于拓扑优化时，优化方案的每一步都需要进行数值计算。

在标准的声学拓扑优化中，插值变量在 0 和 1 之间变化，0 代表空气，1 代表固体。为了给热粘性声学拓扑优化制定相似的插值算法，我想出了一种探试法，具体来讲，就是将热场和粘性场引入到插值策略中。粘性场的两个典型边界条件（参考文献 1）是：

和

上述边界条件有助于我们了解如何执行优化方案，因为前者可以表征空气-固体交界面，后者可表征空气-空气交界面。我们将控制方程写成更一般的形式：

已知对于空气域，(a_v,f_v) = (1,1)，因为它给出了原始方程（1）。如果我们将a_v替换成一个很大的值，梯度项就变得无关紧要；将f_v设为0，可得：

它同诸如固体-空气交界面的无滑边界的边界条件完全一致，只不过是通过控制方程所获得的。我们需要这一性质，因为在优化过程中我们无法应用显式边界条件。因此，固体 (a_v,f_v)的值应该包含 (“large”,0)。由此我们确定了插值的极端值：

和

利用图 3 的测试几何，我对显式边界条件和插值的极端条件进行了对比。左侧使用了边界条件，针对右边的相邻域，我们输入了 a_v 和f_v 的推荐值。

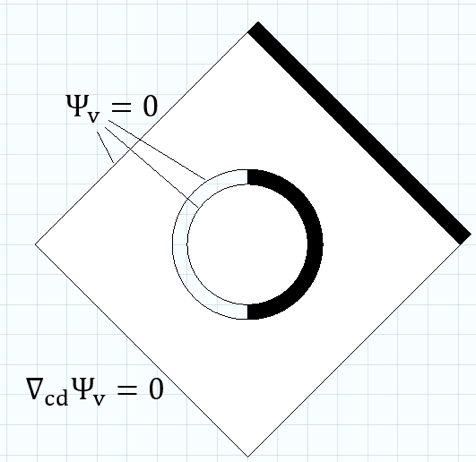
图 3：左侧应用了标准的边界条件。右侧黑色区域表示修改后的、可模拟固体边界的场方程；白色区域表示空气。

我们在边界层足够厚的频率下对所有域的场进行计算，该边界层至少能在视觉上占据部分域。绘图显示场是对称的，这表示极端的场值要么描述空气，要么描述固体。从某种意义上讲，这相当于采用对应的真实的边界条件。

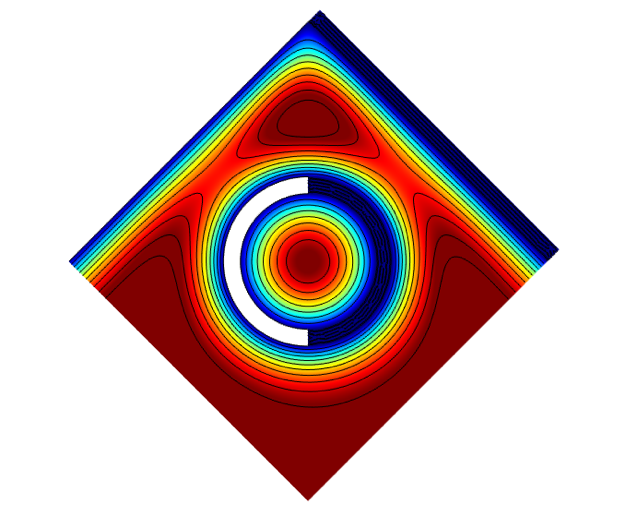
图 4：基于图 3 设置而获得的带等值线的场。

极值条件之间的实际插值是通过 SIMP 或 RAMP 算法（参考文献 2）完成的，就像标准声学拓扑优化一样。粘性场和热场均可通过方程与声压变量建立关联。就这样，我们成功获得了世界上第一个耦合了精确的热粘性损耗的声学拓扑优化算法。

优化损耗声学响应

本节将举例说明优化方法在实际案例中的应用。由于粘性效应，横截面为六角形的管道产生了一定的声学损耗。六角形每边长约为 1.1 mm，其面积相当于半径为 1 mm 的圆形面积。在 100 和 1000 Hz 之间，声学损耗的增长因子将近 2.6，如图 7 所示。现在，我们的目标是找到最优拓扑，在该频率范围内获得更平顺的声学损耗响应，而不考虑实际损耗值。所得结构如下：

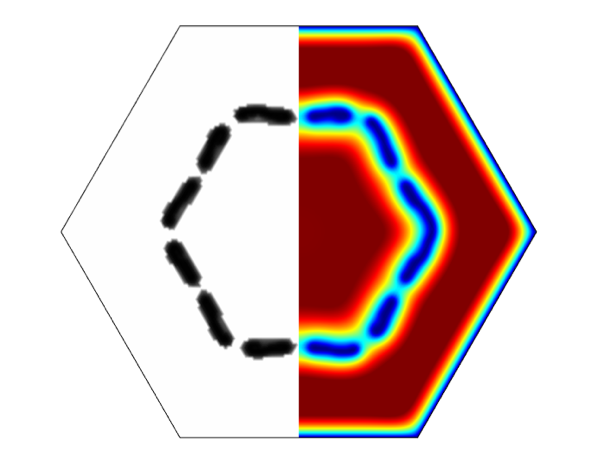
图 5：最大平坦的声学损耗响应的拓扑，及其在 1000 Hz 下的粘性场。

我们创建了一个与优化拓扑相似的简单几何结构，它可以应用显式边界条件。

图 6：优化拓扑的简化表示，及其在 1000 Hz 时的粘性场。

图 7 对比了初始六角形几何和经过拓扑优化的几何的归一化声学损耗。每个管道的损耗被归一化为 100 Hz 的对应值。

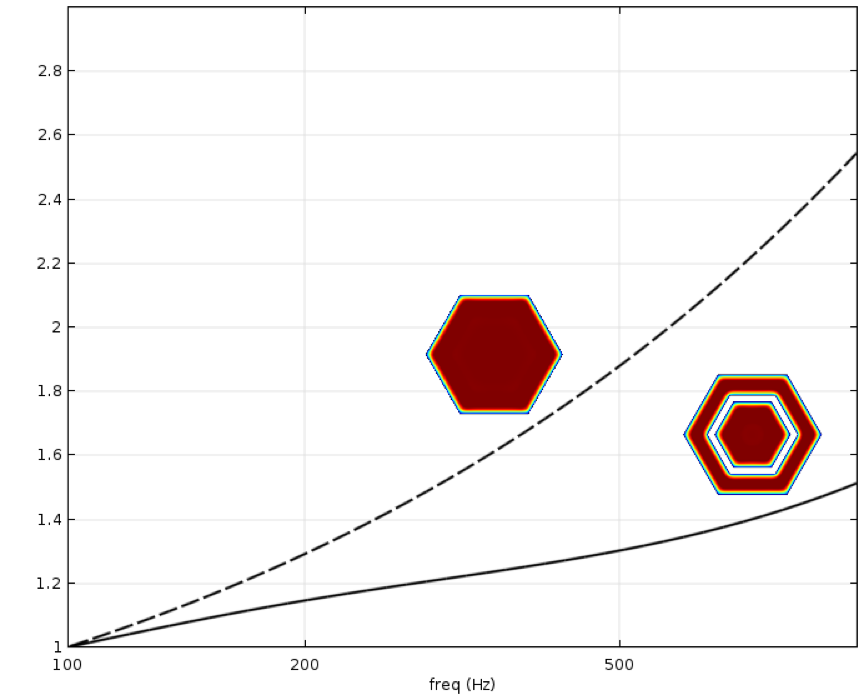
图 7：初始横截面（虚线）和拓扑优化几何（实线）的声学损耗分别被归一化为 100 Hz 的对应值。

优化的拓扑结构在 1000 Hz 下的声学损耗只比 100 Hz 下高出 1.5 倍，而初始的几何结构则高 2.6 倍。就总体的损耗而言，经优化的几何结构明显更高，但如上文提到的，我们在本例中不考虑这一点。

这种新颖的拓扑优化策略可以扩展到更加普遍的一维方法中，使声压可以直接使用在目标函数中。我们确定了通用三维几何结构的拓扑优化方案，不过具体实施仍在进行中。它对于从事微观声学研究工作、致力于改进拓扑优化的高校人士和产业人员大有裨益。我希望该领域将来能够取得更长远的进步。

参考文献

1. W.R. Kampinga, Y.H. Wijnant, A. de Boer, “An Efficient Finite Element Model for Viscothermal Acoustics,” Acta Acoustica united with Acoustica, vol. 97, pp. 618–631, 2011.
2. M.P. Bendsoe, O. Sigmund, Topology Optimization: Theory, Methods, and Applications, Springer, 2003.

特邀作者简介

René Christensen 在振动噪声领域拥有十多年工作经验，曾担任顾问（iCapture ApS）和助听器行业的工程师（Oticon A/S，GN Hearing A/S）。他对微观声学中的粘热效应的建模尤其感兴趣，这也是他的博士研究课题。2015 年，René 作为高级声学工程师加入了 GN Hearing 公司的硬件平台研发声学团队，主要负责助听器的设计和优化。